Assignment 1: Software Setup

Overview

In this course, there will be (roughly) one assignment per week. The purpose of these assignments is to familiarize you with the main course topic. One novel point is that all these assignments will be finished in a mechanized way, that is, you will finish them using some tools. The tools used in this course are Coq, Z3, etc..

This is the first assignment, in Part A and B, you are required to install all the necessary tools and software, and have some ideas of how they work and how to use them. In Part C，you're going to solve several problems as a Python warming up. Some problems are tagged with Exercise, which you should solve. And one problem is tagged with Challenge, which is optional. For any problems, feel free to ask the TAs for help.

Hand-in Procedure

When you finished the assignment, zip you code files (exclude .venv folder) with file name studentid-assignment1.zip (e.g SA19225111-assignment1.zip), and submit it to Graduate Information Platform. The deadline is 11:59PM of 6th April 2021 (Beijing time). Any late submission will NOT be accepted.

Part A: Coq

Coq is a famous and also widely used formal proof management system. It provides a formal language to write mathematical definitions, executable algorithms and theorems together with an environment for semi-interactive development of machine-checked proofs. See more information about Coq, and documentation of Coq.

In this class, we will do theorem proving for propositional logic, predicate logic and constructive logic in Coq.

Coq Installation

We'll use the latest Coq version 8.12.0, and the installation instructions for different platforms can be found here.

Coq Warming Up

To validate your Coq installation, you can try the following warm-up. Download the warm-up sample code, Open your Coq IDE and open the above code file.
After click Go to end Button, you will get the following output:

  = monday
  : day
  = tuesday
  : day

Part B: Z3

Z3 is a theorem prover/solver from Microsoft Research. In this course, you'll solve SAT & SMT problems using Z3, and also you will have the opportunity to solve many realistic problems using Z3: say, program verification, symbolic execution, reversing engineering from information security, etc.. For more information about Z3, you can check it's project homepage.

Python Installation

In this course, we recommend you to use the Python Binding of Z3 (we'll be using the Python binding to send out the assignments. Of course, there are other bindings for Z3, say OCaml or .Net bindings, if you want to use these bindings, talk to the TAs in advance). You can download Python installation package from official site. We recommend Python 3.7 or higher version, but if you want to manage multiple versions of Python, try pyenv or anaconda.

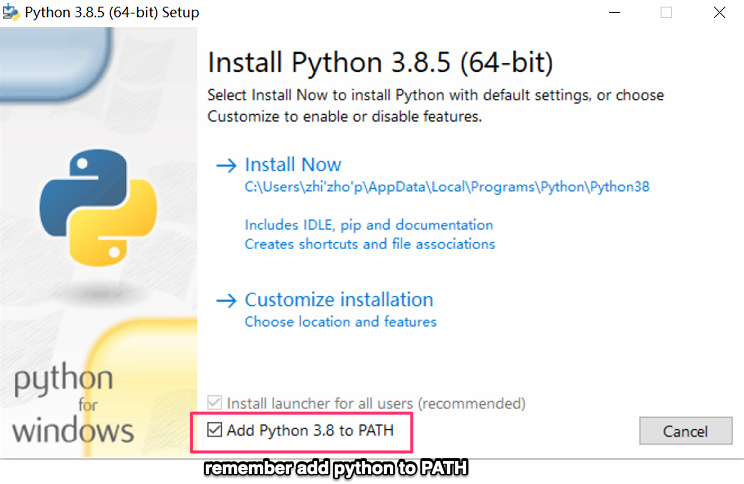
tips: if you are using Windows, please remember add your Python binary to the PATH environment. The figure below demonstrates what you should do at installation time：

Z3Py Installation

The Z3Py package is the Z3 API in Python (Z3 also has the C, .Net and OCaml APIs). The next steps show you two ways to install Z3Py package. Actually, both of them are depend on pip.

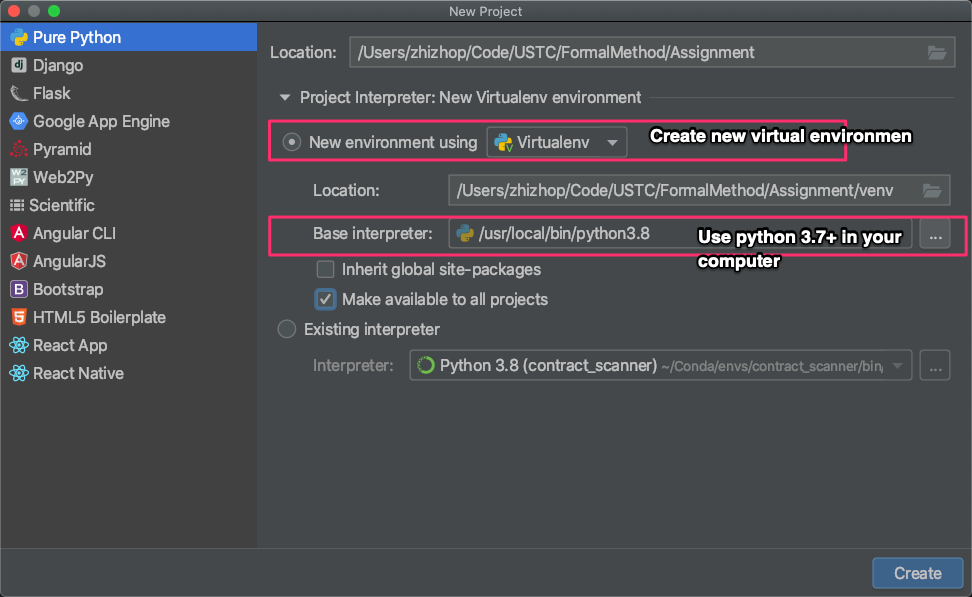
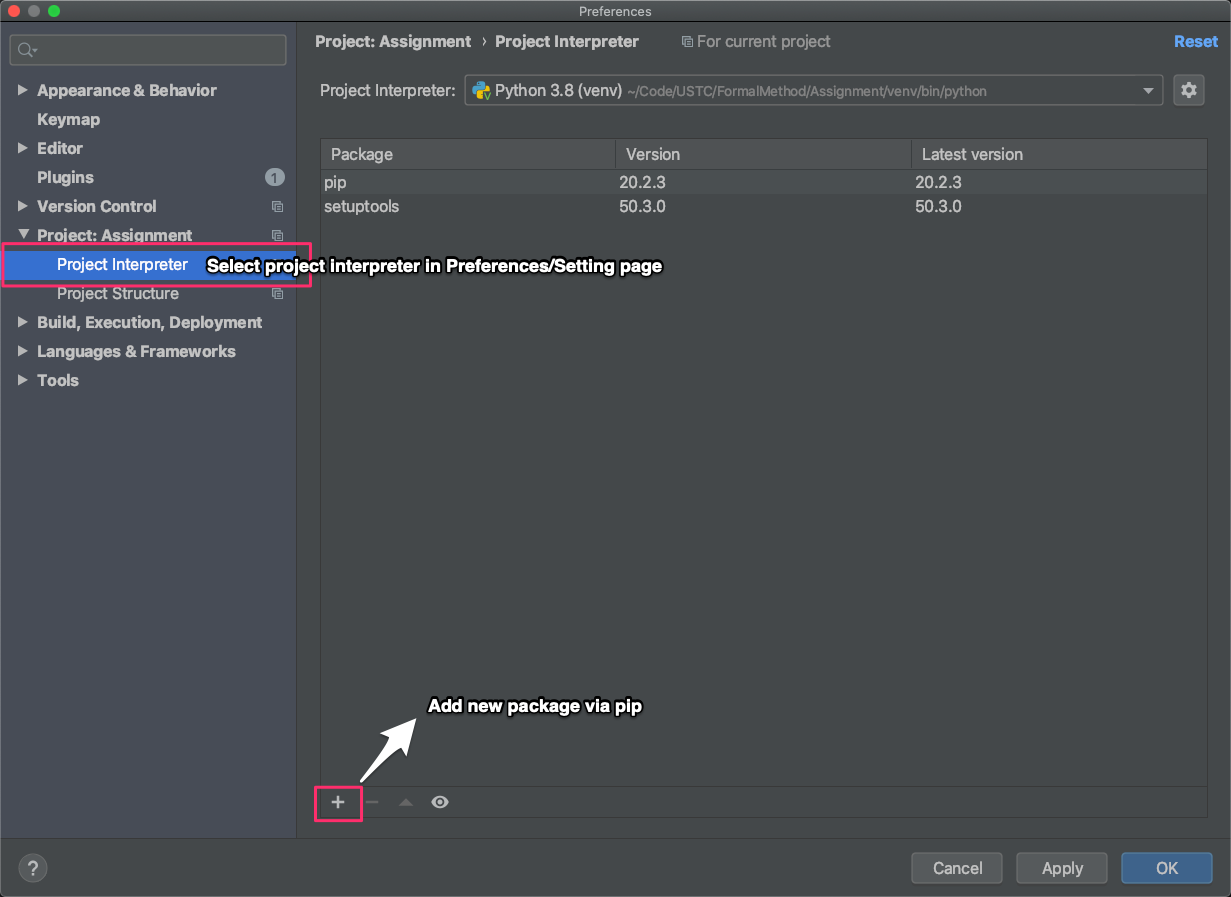
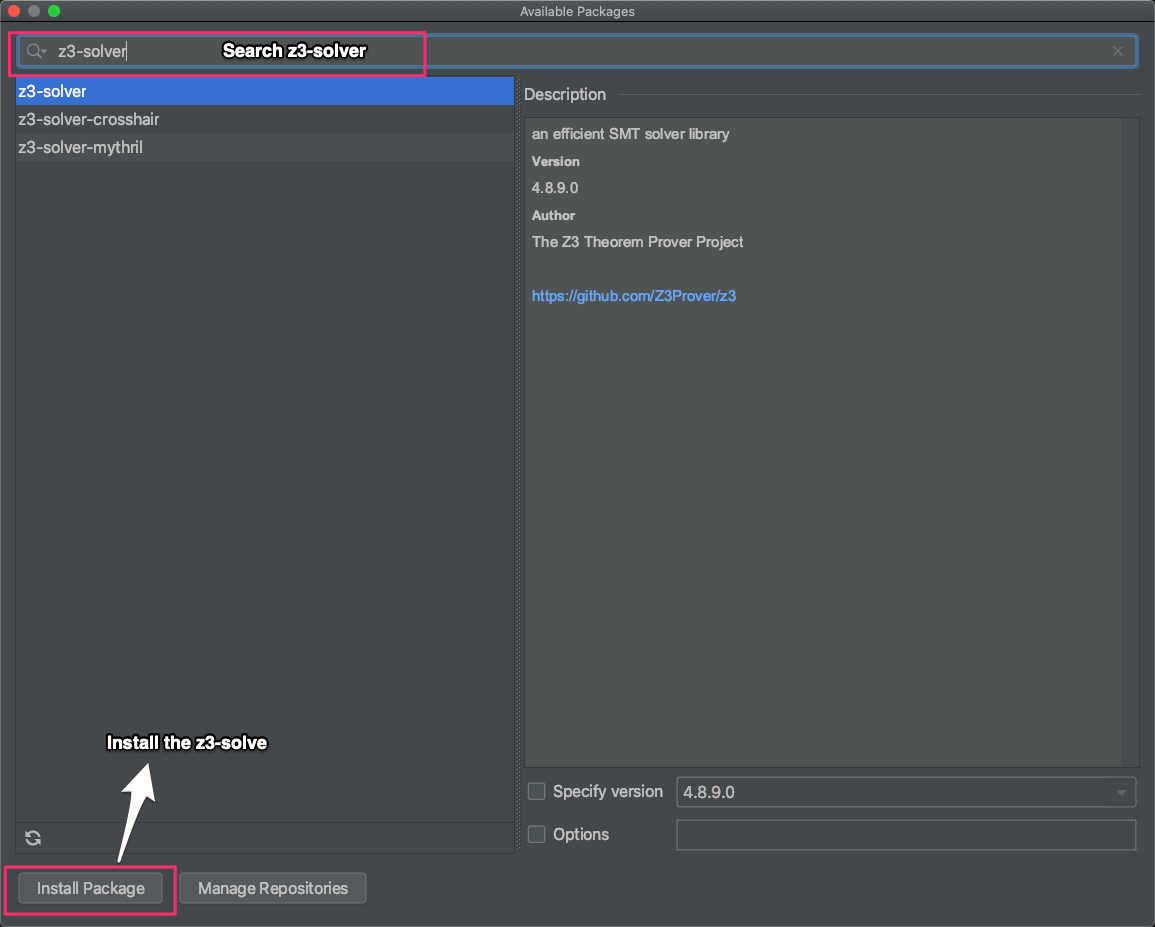
PyCharm (recommended):

PyCharm is one popular Python IDE, it can effectively manage your Python development environment. You can download PyCharm from the official website. you can use the community edition for free or register an account with your USTC email to get education-free license for professional edition.

After the the PyCharm is installed, you can follow the following steps to install Z3Py:

Create project with virtualenv:

Select project interpreter in preferences page:

Search and install the z3-solver package:

Command line:

If you prefer to use command line, it's also recommended to use virtualenv to manage Python environment.

Install virtualenv via pip

$ python -m pip install --user virtualenv

Use virtualenv to create a environment
```
$ python -m venv formal_method
```
Activate the new environment
```
$ source formal_method/bin/activate
```
Install the z3-solver package in the environment
```
$ pip install z3-solver
```

Z3 Warming Up

To make sure you have install Z3 correctly, we provide a simple test case for you to test your installation.

View this simple logical proposition. And we want to get the solution that make it satisfiable (i.e., let it be True):

    P /\ Q

Download this code and run it.

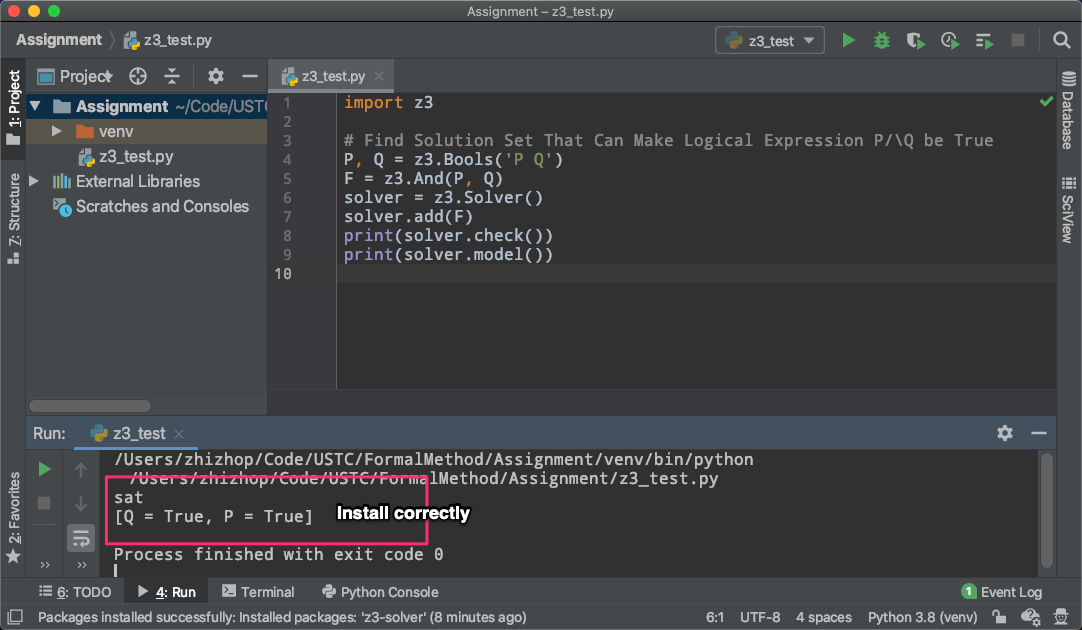
If Z3 is installed correctly, z3_test.py will run without any error and the output should look like:

Part C: Python Warming Up

Python is a widely used programming language and is easy to learn and use. Most of our assignments are written in Python, so if you have not used Python before, be sure to spend some time learning the basic syntax or the Python tutorial.

This and the future assignments will use AST (abstract syntax tree) to encode formal languages. To let you get familiarized yourself with the creation and operations on AST.In this part, you'll implement a very simple arithmetic calculator in Python.

The syntax for the calculator language is described by the following context-free grammar (CFG):

    exp ::= num
          | exp + exp
          | exp - exp
          | exp * exp
          | exp / exp
          | (exp)

The expressions generated from the CFG above can be represented by trees. For instance, the expression 3 * 4 + 10 / 2 to AST like:

                +
              /   \
             /     \
            *       /
           / \     /  \
          /   \   /    \
         3    4  10     2

Exercise 1: Download this code template and fill in the missing data structures in it. You also need to implement the __str__() method in these classes to print the necessary information. Make sure your code pass the unit tests 1&2.

Based on the AST data structures, we can implement various computations on the AST. One special and important operation you'll be building is an interpreter. Simply speaking, an interpreter reads in some program as input, and output its result. Consider again the example 3 * 4 + 10 / 2, the interpreter will output 17>.

Exercise 2: Finish the interpreter by filling in the missing code in the eval_value() function. Don't forget to test your code using unit tests 3&4.

Challenge: For simplicity，our test cases are written by AST manually. In most cases, AST is generated by processing source code file, the programme do these work called lexer and parser. Try to implement a lexer/parser that reads the algebraic expressions from a file and generates the AST automatically. Consider to use some tools, if you don't want to write everything from scratch.

Which Coq IDE to use?

The official IDE to edit Coq source code is "CoqIde", which comes with Coq. It's great and you may try it.

There is another popular IDE (my favorite): Proof General, and it's more popular in the Coq community. You may try it.

The installation of proof general is simple:

Ubuntu/Debian:

  $ sudo apt-get install proofgeneral
  $ sudo apt-get install proofgeneral-coq

Windows:there is a pre-built version hacked by us based on GNU emacs. You should uncompress this archive and put it at (important!):
```
  d:\emacs-23.1
```
And it also assumes the Coq executable is at "C:\program files\Coq\bin", if that's not the case, change the file "d:\emacs-23.1\bin\coq-emacs.bat" accordingly.

There are only a few commands you need to know to use ProofGeneral effectively. They are:

C-c C-n: send the next command to Coq.
C-c C-u: undo (retract) the most recently executed command.
C-c C-RET: submit everything up to the current cursor location to Coq for processing.
C-c C-.: move the cursor to the end of the last command which has been processed by Coq.
C-c . : toggle "electric terminator mode". When this mode is turned on, simply typing a period will send the current command to Coq (normally you have to type a period and then type C-c C-n).

This finishes the assignment, zip you code files (exclude .venv folder) with file name studentid-assignment1.zip (e.g SA19225111-assignment1.zip), and submit it to Graduate Information Platform..

Have fun!