We can also view an algorithm as a tool for solving a well-specified computational problem. The statement of the problem specifies in general terms the desired input/output relationship. The algorithm describes a specific computational procedure for achieving that input/output relationship.
We begin our study of algorithms with the problem of sorting a sequence of numbers into nondecreasing order. This problem arises frequently in practice and provides fertile ground for introducing many standard design techniques and analysis tools. Here is how we formally define the sorting problem:
Input: A sequence of n numbers
Output: A permutation (reordering)
Given an input sequence such as
Sorting is a fundamental operation in computer science (many programs use it as an intermediate step), and as a result a large number of good sorting algorithms have been developed. Which algorithm is best for a given application depends on the number of items to be sorted, the extent to which the items are already somewhat sorted, and the kind of storage device to be used: main memory, disks, or tapes.
An algorithm is said to be correct if, for every input instance, it halts with the correct output. We say that a correct algorithm solves the given computational problem. An incorrect algorithm might not halt at all on some input instances, or it might halt with other than the desired answer. Contrary to what one might expect, incorrect algorithms can sometimes be useful, if their error rate can be controlled. We shall see an example of this in Chapter 33 when we study algorithms for finding large prime numbers. Ordinarily, however, we shall be concerned only with correct algorithms.
An algorithm can be specified in English, as a computer program, or even as a hardware design. The only requirement is that the specification must provide a precise description of the computational procedure to be followed.
In this book, we shall typically describe algorithms as programs written in a pseudocode that is very much like C, Pascal, or Algol. If you have been introduced to any of these languages, you should have little trouble reading our algorithms. What separates pseudocode from "real" code is that in pseudocode, we employ whatever expressive method is most clear and concise to specify a given algorithm. Sometimes, the clearest method is English, so do not be surprised if you come across an English phrase or sentence embedded within a section of "real" code. Another difference between pseudocode and real code is that pseudocode is not typically concerned with issues of software engineering. Issues of data abstraction, modularity, and error handling are often ignored in order to convey the essence of the algorithm more concisely.
We start with insertion sort, which is an efficient algorithm for sorting a small number of elements. Insertion sort works the way many people sort a bridge or gin rummy hand. We start with an empty left hand and the cards face down on the table. We then remove one card at a time from the table and insert it into the correct position in the left hand. To find the correct position for a card, we compare it with each of the cards already in the hand, from right to left, as illustrated in Figure 1.1.
Our pseudocode for insertion sort is presented as a procedure called INSERTION-SORT, which takes as a parameter an array A[1 . . n] containing a sequence of length n that is to be sorted. (In the code, the number n of elements in A is denoted by length[A].) The input numbers are sorted in place: the numbers are rearranged within the array A, with at most a constant number of them stored outside the array at any time. The input array A contains the sorted output sequence when INSERTION-SORT is finished.
Figure 1.2 shows how this algorithm works for A =
We use the following conventions in our pseudocode.
1. Indentation indicates block structure. For example, the body of the for loop that begins on line 1 consists of lines 2-8, and the body of the while loop that begins on line 5 contains lines 6-7 but not line 8. Our indentation style applies to if-then-else statements as well. Using indentation instead of conventional indicators of block structure, such as begin and end statements, greatly reduces clutter while preserving, or even enhancing, clarity.1
1 In real programming languages, it is generally not advisable to use indentation alone to indicate block structure, since levels of indentation are hard to determine when code is split across pages.
2. The looping constructs while, for, and repeat and the conditional constructs if, then, and else have the the same interpretation as in Pascal.
3. The symbol
4. A multiple assignment of the form i
5. Variables (such as i, j, and key) are local to the given procedure. We shall not use global variables without explicit indication.
6. Array elements are accessed by specifying the array name followed by the index in square brackets. For example, A[i] indicates the ith element of the array A. The notation ". ." is used to indicate a range of values within an array. Thus, A[1. . j] indicates the subarray of A consisting of elements A[1], A[2], . . . , A[j].
7. Compound data are typically organized into objects, which are comprised of attributes or fields. A particular field is accessed using the field name followed by the name of its object in square brackets. For example, we treat an array as an object with the attribute length indicating how many elements it contains. To specify the number of elements in an array A, we write length[A]. Although we use square brackets for both array indexing and object attributes, it will usually be clear from the context which interpretation is intended.
A variable representing an array or object is treated as a pointer to the data representing the array or object. For all fields f of an object x, setting y
Sometimes, a pointer will refer to no object at all. In this case, we give it the special value NIL.
8. Parameters are passed to a procedure by value: the called procedure receives its own copy of the parameters, and if it assigns a value to a parameter, the change is not seen by the calling routine. When objects are passed, the pointer to the data representing the object is copied, but the object's fields are not. For example, if x is a parameter of a called procedure, the assignment x
1.1-1
Using Figure 1.2 as a model, illustrate the operation of INSERTION-SORT on the array A =
1.1-2
Rewrite the INSERTION-SORT procedure to sort into nonincreasing instead of nondecreasing order.
1.1-3
Consider the searching problem:
Input: A sequence of n numbers A =
Output: An index i such that v = A[i] or the special value NIL if v does not appear in A.
Write pseudocode for linear search, which scans through the sequence, looking for v.
1.1-4
Consider the problem of adding two n-bit binary integers, stored in two n-element arrays A and B. The sum of the two integers should be stored in binary form in an (n + 1)-element array C. State the problem formally and write pseudocode for adding the two integers.
Analyzing an algorithm has come to mean predicting the resources that the algorithm requires. Occasionally, resources such as memory, communication bandwidth, or logic gates are of primary concern, but most often it is computational time that we want to measure. Generally, by analyzing several candidate algorithms for a problem, a most efficient one can be easily identified. Such analysis may indicate more than one viable candidate, but several inferior algorithms are usually discarded in the process.
Before we can analyze an algorithm, we must have a model of the implementation technology that will be used, including a model for the resources of that technology and their costs. For most of this book, we shall assume a generic one-processor, random-access machine (RAM) model of computation as our implementation technology and understand that our algorithms will be implemented as computer programs. In the RAM model, instructions are executed one after another, with no concurrent operations. In later chapters, however, we shall have occasion to investigate models for parallel computers and digital hardware.
Analyzing even a simple algorithm can be a challenge. The mathematical tools required may include discrete combinatorics, elementary probability theory, algebraic dexterity, and the ability to identify the most significant terms in a formula. Because the behavior of an algorithm may be different for each possible input, we need a means for summarizing that behavior in simple, easily understood formulas.
Even though we typically select only one machine model to analyze a given algorithm, we still face many choices in deciding how to express our analysis. One immediate goal is to find a means of expression that is simple to write and manipulate, shows the important characteristics of an algorithm's resource requirements, and suppresses tedious details.
The time taken by the INSERTION-SORT procedure depends on the input: sorting a thousand numbers takes longer than sorting three numbers. Moreover, INSERTION-SORT can take different amounts of time to sort two input sequences of the same size depending on how nearly sorted they already are. In general, the time taken by an algorithm grows with the size of the input, so it is traditional to describe the running time of a program as a function of the size of its input. To do so, we need to define the terms "running time" and "size of input" more carefully.
The best notion for input size depends on the problem being studied. For many problems, such as sorting or computing discrete Fourier transforms, the most natural measure is the number of items in the input--for example, the array size n for sorting. For many other problems, such as multiplying two integers, the best measure of input size is the total number of bits needed to represent the input in ordinary binary notation. Sometimes, it is more appropriate to describe the size of the input with two numbers rather than one. For instance, if the input to an algorithm is a graph, the input size can be described by the numbers of vertices and edges in the graph. We shall indicate which input size measure is being used with each problem we study.
The running time of an algorithm on a particular input is the number of primitive operations or "steps" executed. It is convenient to define the notion of step so that it is as machine-independent as possible. For the moment, let us adopt the following view. A constant amount of time is required to execute each line of our pseudocode. One line may take a different amount of time than another line, but we shall assume that each execution of the ith line takes time ci, where ci is a constant. This viewpoint is in keeping with the RAM model, and it also reflects how the pseudocode would be implemented on most actual computers.2
2There are some subtleties here. Computational steps that we specify in English are often variants of a procedure that requires more than just a constant amount of time. For example, later in this book we might say "sort the points by x-coordinate," which, as we shall see, takes more than a constant amount of time. Also, note that a statement that calls a subroutine takes constant time, though the subroutine, once invoked, may take more. That is, we separate the process of calling the subroutine--passing parameters to it, etc.--from the process of executing the subroutine.
In the following discussion, our expression for the running time of INSERTION-SORT will evolve from a messy formula that uses all the statement costs ci to a much simpler notation that is more concise and more easily manipulated. This simpler notation will also make it easy to determine whether one algorithm is more efficient than another.
We start by presenting the INSERTION-SORT procedure with the time "cost" of each statement and the number of times each statement is executed. For each j = 2, 3, . . . , n, where n = length[A], we let tj be the number of times the while loop test in line 5 is executed for that value of j. We assume that comments are not executable statements, and so they take no time.
The running time of the algorithm is the sum of running times for each statement executed; a statement that takes ci steps to execute and is executed n times will contribute ci n to the total running time.3 To compute T(n), the running time of INSERTION-SORT, we sum the products of the cost and times columns, obtaining
3This characteristic does not necessarily hold for a resource such as memory. A statement that references m words of memory and is executed n times does not necessarily consume mn words of memory in total.
Even for inputs of a given size, an algorithm's running time may depend on which input of that size is given. For example, in INSERTION-SORT, the best case occurs if the array is already sorted. For each j = 2, 3, . . . , n, we then find that A[i]
This running time can be expressed as an + b for constants a and b that depend on the statement costs ci; it is thus a linear function of n.
If the array is in reverse sorted order--that is, in decreasing order--the worst case results. We must compare each element A[j] with each element in the entire sorted subarray A[1. . j - 1], and so tj = j for j = 2,3, . . . , n. Noting that
and
(we shall review these summations in Chapter 3), we find that in the worst case, the running time of INSERTION-SORT is
This worst-case running time can be expressed as an2 + bn+ c for constants a, b, and c that again depend on the statement costs ci; it is thus a quadratic function of n.
Typically, as in insertion sort, the running time of an algorithm is fixed for a given input, although in later chapters we shall see some interesting "randomized" algorithms whose behavior can vary even for a fixed input.
In our analysis of insertion sort, we looked at both the best case, in which the input array was already sorted, and the worst case, in which the input array was reverse sorted. For the remainder of this book, though, we shall usually concentrate on finding only the worst-case running time, that is, the longest running time for any input of size n. We give three reasons for this orientation.
In some particular cases, we shall be interested in the average-case or expected running time of an algorithm. One problem with performing an average-case analysis, however, is that it may not be apparent what constitutes an "average" input for a particular problem. Often, we shall assume that all inputs of a given size are equally likely. In practice, this assumption may be violated, but a randomized algorithm can sometimes force it to hold.
We have used some simplifying abstractions to ease our analysis of the INSERTION-SORT procedure. First, we ignored the actual cost of each statement, using the constants ci to represent these costs. Then, we observed that even these constants give us more detail than we really need: the worst-case running time is an2 + bn + c for some constants a, b, and c that depend on the statement costs ci. We thus ignored not only the actual statement costs, but also the abstract costs ci.
We shall now make one more simplifying abstraction. It is the rate of growth, or order of growth, of the running time that really interests us. We therefore consider only the leading term of a formula (e.g., an2), since the lower-order terms are relatively insignificant for large n. We also ignore the leading term's constant coefficient, since constant factors are less significant than the rate of growth in determining computational efficiency for large inputs. Thus, we write that insertion sort, for example, has a worst-case running time of
We usually consider one algorithm to be more efficient than another if its worst-case running time has a lower order of growth. This evaluation may be in error for small inputs, but for large enough inputs a
1.2-1
Consider sorting n numbers stored in array A by first finding the smallest element of A and putting it in the first entry of another array B. Then find the second smallest element of A and put it in the second entry of B. Continue in this manner for the n elements of A. Write pseudocode for this algorithm, which is known as selection sort. Give the best-case and worst-case running times of selection sort in
1.2-2
Consider linear search again (see Exercise 1.1-3). How many elements of the input sequence need to be checked on the average, assuming that the element being searched for is equally likely to be any element in the array? How about in the worst case? What are the average-case and worst-case running times of linear search in
1.2-3
Consider the problem of determining whether an arbitrary sequence
1.2-4
Consider the problem of evaluating a polynomial at a point. Given n coefficients a0, a1, . . . , an - 1 and a real number x, we wish to compute
1.2-5
Express the function n3/1000 - 100n2 - 100n + 3 in terms of
1.2-6
How can we modify almost any algorithm to have a good best-case running time?
There are many ways to design algorithms. Insertion sort uses an incremental approach: having sorted the subarray A[1 . . j - 1], we insert the single element A[j] into its proper place, yielding the sorted subarray A[1 . . j].
In this section, we examine an alternative design approach, known as "divide-and-conquer." We shall use divide-and-conquer to design a sorting algorithm whose worst-case running time is much less than that of insertion sort. One advantage of divide-and-conquer algorithms is that their running times are often easily determined using techniques that will be introduced in Chapter 4.
Many useful algorithms are recursive in structure: to solve a given problem, they call themselves recursively one or more times to deal with closely related subproblems. These algorithms typically follow a divide-and-conquer approach: they break the problem into several subproblems that are similar to the original problem but smaller in size, solve the subproblems recursively, and then combine these solutions to create a solution to the original problem.
The divide-and-conquer paradigm involves three steps at each level of the recursion:
Divide the problem into a number of subproblems.
Conquer the subproblems by solving them recursively. If the subproblem sizes are small enough, however, just solve the subproblems in a straightforward manner.
Combine the solutions to the subproblems into the solution for the original problem.
The merge sort algorithm closely follows the divide-and-conquer paradigm. Intuitively, it operates as follows.
Divide: Divide the n-element sequence to be sorted into two subsequences of n/2 elements each.
Conquer: Sort the two subsequences recursively using merge sort.
Combine: Merge the two sorted subsequences to produce the sorted answer.
We note that the recursion "bottoms out" when the sequence to be sorted has length 1, in which case there is no work to be done, since every sequence of length 1 is already in sorted order.
The key operation of the merge sort algorithm is the merging of two sorted sequences in the "combine" step. To perform the merging, we use an auxiliary procedure MERGE(A,p,q,r), where A is an array and p, q, and r are indices numbering elements of the array such that p
Although we leave the pseudocode as an exercise (see Exercise 1.3-2), it is easy to imagine a MERGE procedure that takes time
We can now use the MERGE procedure as a subroutine in the merge sort algorithm. The procedure MERGE-SORT(A,p,r) sorts the elements in the subarray A[p. .r]. If p
4The expression
To sort the entire sequence A =
When an algorithm contains a recursive call to itself, its running time can often be described by a recurrence equation or recurrence, which describes the overall running time on a problem of size n in terms of the running time on smaller inputs. We can then use mathematical tools to solve the recurrence and provide bounds on the performance of the algorithm.
A recurrence for the running time of a divide-and-conquer algorithm is based on the three steps of the basic paradigm. As before, we let T(n) be the running time on a problem of size n. If the problem size is small enough, say n
In Chapter 4, we shall see how to solve common recurrences of this form.
Although the pseudocode for MERGE-SORT works correctly when the number of elements is not even, our recurrence-based analysis is simplified if we assume that the original problem size is a power of two. Each divide step then yields two subsequences of size exactly n/2. In Chapter 4, we shall see that this assumption does not affect the order of growth of the solution to the recurrence.
We reason as follows to set up the recurrence for T(n), the worst-case running time of merge sort on n numbers. Merge sort on just one element takes constant time. When we have n > 1 elements, we break down the running time as follows.
Divide: The divide step just computes the middle of the subarray, which takes constant time. Thus, D(n) =
Conquer: We recursively solve two subproblems, each of size n/2, which contributes 2T(n/2) to the running time.
Combine: We have already noted that the MERGE procedure on an n-element subarray takes time
When we add the functions D(n) and C(n) for the merge sort analysis, we are adding a function that is
In Chapter 4, we shall show that T(n) is
1.3-1
Using Figure 1.3 as a model, illustrate the operation of merge sort on the array A =
1.3-2
Write pseudocode for MERGE(A,p,q,r).
1.3-3
Use mathematical induction to show that the solution of the recurrence
1.3-4
Insertion sort can be expressed as a recursive procedure as follows. In order to sort A[1 . . n], we recursively sort A[1 . . n - 1] and then insert A[n] into the sorted array A[1 . . n - 1]. Write a recurrence for the running time of this recursive version of insertion sort.
1.3-5
Referring back to the searching problem (see Exercise 1.1-3), observe that if the sequence A is sorted, we can check the midpoint of the sequence against v and eliminate half of the sequence from further consideration. Binary search is an algorithm that repeats this procedure, halving the size of the remaining portion of the sequence each time. Write pseudocode, either iterative or recursive, for binary search. Argue that the worst-case running time of binary search is
1.3-6
Observe that the while loop of lines 5-7 of the INSERTION-SORT procedure in Section 1.1 uses a linear search to scan (backward) through the sorted subarray A[1 . . j - 1]. Can we use a binary search (see Exercise 1.3-5) instead to improve the overall worst-case running time of insertion sort to
1.3-7
Describe a
A good algorithm is like a sharp knife--it does exactly what it is supposed to do with a minimum amount of applied effort. Using the wrong algorithm to solve a problem is like trying to cut a steak with a screwdriver: you may eventually get a digestible result, but you will expend considerably more effort than necessary, and the result is unlikely to be aesthetically pleasing.
Algorithms devised to solve the same problem often differ dramatically in their efficiency. These differences can be much more significant than the difference between a personal computer and a supercomputer. As an example, let us pit a supercomputer running insertion sort against a small personal computer running merge sort. They each must sort an array of one million numbers. Suppose the supercomputer executes 100 million instructions per second, while the personal computer executes only one million instructions per second. To make the difference even more dramatic, suppose that the world's craftiest programmer codes insertion sort in machine language for the supercomputer, and the resulting code requires 2n2 supercomputer instructions to sort n numbers. Merge sort, on the other hand, is programmed for the personal computer by an average programmer using a high-level language with an inefficient compiler, with the resulting code taking 50n 1g n personal computer instructions. To sort a million numbers, the supercomputer takes
By using an algorithm whose running time has a lower order of growth, even with a poor compiler, the personal computer runs 20 times faster than the supercomputer!
This example shows that algorithms, like computer hardware, are a technology. Total system performance depends on choosing efficient algorithms as much as on choosing fast hardware. Just as rapid advances are being made in other computer technologies, they are being made in algorithms as well.
1.4-1
Suppose we are comparing implementations of insertion sort and merge sort on the same machine. For inputs of size n, insertion sort runs in 8n2 steps, while merge sort runs in 64n 1g n steps. For which values of n does insertion sort beat merge sort? How might one rewrite the merge sort pseudocode to make it even faster on small inputs?
1.4-2
What is the smallest value of n such that an algorithm whose running time is 100n2 runs faster than an algorithm whose running time is 2n on the same machine?
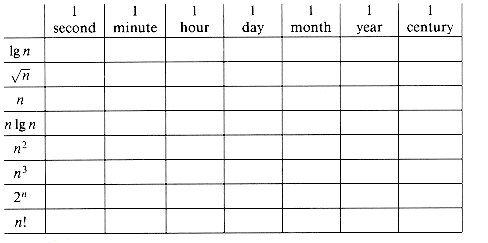
1-1 Comparison of running times
For each function f(n) and time t in the following table, determine the largest size n of a problem that can be solved in time t, assuming that the algorithm to solve the problem takes f(n) microseconds.
1-2 Insertion sort on small arrays in merge sort
Although merge sort runs in
a. Show that the n/k sublists, each of length k, can be sorted by insertion sort in
b. Show that the sublists can be merged in
c. Given that the modified algorithm runs in
d. How should k be chosen in practice?
1-3 Inversions
Let A[1 . . n] be an array of n distinct numbers. If i < j and A[i] > A[j], then the pair (i, j) is called an inversion of A.
a. List the five inversions of the array
b. What array with elements from the set { 1,2, . . . , n} has the most inversions? How many does it have?
c. What is the relationship between the running time of insertion sort and the number of inversions in the input array? Justify your answer.
d. Give an algorithm that determines the number of inversions in any permutation on n elements in
There are many excellent texts on the general topic of algorithms, including those by Aho, Hopcroft, and Ullman[4, 5], Baase [14], Brassard and Bratley [33], Horowitz and Sahni [105], Knuth[121, 122, 123], Manber [142], Mehlhorn[144, 145, 146], Purdom and Brown [164], Reingold, Nievergelt, and Deo [167], Sedgewick [175], and Wilf [201]. Some of the more practical aspects of algorithm design are discussed by Bentley[24, 25] and Gonnet [90].
In 1968, Knuth published the first of three volumes with the general title The Art of Computer Programming[121, 122, 123]. The first volume ushered in the modern study of computer algorithms with a focus on the analysis of running time, and the full series remains an engaging and worthwhile reference for many of the topics presented here. According to Knuth, the word "algorithm" is derived from the name "al-Khowârizmî," a ninth-century Persian mathematician.
Aho, Hopcroft, and Ullman [4] advocated the asymptotic analysis of algorithms as a means of comparing relative performance. They also popularized the use of recurrence relations to describe the running times of recursive algorithms.
Knuth [123] provides an encyclopedic treatment of many sorting algorithms. His comparison of sorting algorithms (page 381) includes exact step-counting analyses, like the one we performed here for insertion sort. Knuth's discussion of insertion sort encompasses several variations of the algorithm. The most important of these is Shell's sort, introduced by D. L. Shell, which uses insertion sort on periodic subsequences of the input to produce a faster sorting algorithm.
Merge sort is also described by Knuth. He mentions that a mechanical collator capable of merging two decks of punched cards in a single pass was invented in 1938. J. von Neumann, one of the pioneers of computer science, apparently wrote a program for merge sort on the EDVAC computer in 1945.
 a1, a2, . . . , an
a1, a2, . . . , an .
. of the input sequence such that
of the input sequence such that  .
. 31, 41, 59, 26, 41, 58
31, 41, 59, 26, 41, 58 , a sorting algorithm returns as output the sequence
, a sorting algorithm returns as output the sequence  26, 31, 41, 41, 58, 59
26, 31, 41, 41, 58, 59 . Such an input sequence is called an instance of the sorting problem. In general, an instance of a problem consists of all the inputs (satisfying whatever constraints are imposed in the problem statement) needed to compute a solution to the problem.
. Such an input sequence is called an instance of the sorting problem. In general, an instance of a problem consists of all the inputs (satisfying whatever constraints are imposed in the problem statement) needed to compute a solution to the problem.Insertion sort

Figure 1.1 Sorting a hand of cards using insertion sort.
INSERTION-SORT (A)
1 for j
 2 to length[A]
2 to length[A]2 do key
 A[j]
A[j]3
 Insert A[j] into the sorted sequence A[1 . . j - 1].
Insert A[j] into the sorted sequence A[1 . . j - 1].4 i
 j - 1
j - 15 while i > 0 and A[i] > key
6 do A[i + 1]
 A[i]
A[i]7 i
 i - 1
i - 18 A[i + 1]
 key
key 5, 2, 4, 6, 1, 3
5, 2, 4, 6, 1, 3 . The index j indicates the "current card" being inserted into the hand. Array elements A[1.. j - 1] constitute the currently sorted hand, and elements A[j + 1 . . n] correspond to the pile of cards still on the table. The index j moves left to right through the array. At each iteration of the "outer" for loop, the element A[j] is picked out of the array (line 2). Then, starting in position j - 1, elements are successively moved one position to the right until the proper position for A[j] is found (lines 4-7), at which point it is inserted (line 8).
. The index j indicates the "current card" being inserted into the hand. Array elements A[1.. j - 1] constitute the currently sorted hand, and elements A[j + 1 . . n] correspond to the pile of cards still on the table. The index j moves left to right through the array. At each iteration of the "outer" for loop, the element A[j] is picked out of the array (line 2). Then, starting in position j - 1, elements are successively moved one position to the right until the proper position for A[j] is found (lines 4-7), at which point it is inserted (line 8).
Figure 1.2 The operation of INSERTION-SORT on the array A =
 5, 2, 4, 6, 1, 3
5, 2, 4, 6, 1, 3 . The position of index j is indicated by a circle.
. The position of index j is indicated by a circle.Pseudocode conventions
 indicates that the remainder of the line is a comment.
indicates that the remainder of the line is a comment.  j
j  e assigns to both variables i and j the value of expression e; it should be treated as equivalent to the assignment j
e assigns to both variables i and j the value of expression e; it should be treated as equivalent to the assignment j  e followed by the assignment i
e followed by the assignment i  j.
j. x causes f[y] = f[x]. Moreover, if we now set f[x]
x causes f[y] = f[x]. Moreover, if we now set f[x]  3, then afterward not only is f[x] = 3, but f[y] = 3 as well. In other words, x and y point to ("are") the same object after the assignment y
3, then afterward not only is f[x] = 3, but f[y] = 3 as well. In other words, x and y point to ("are") the same object after the assignment y  x.
x. y within the called procedure is not visible to the calling procedure. The assignment f[x]
y within the called procedure is not visible to the calling procedure. The assignment f[x]  3, however, is visible.
3, however, is visible.Exercises
 31, 41, 59, 26, 41, 58
31, 41, 59, 26, 41, 58 .
. a1, a2, . . . ,an
a1, a2, . . . ,an and a value v.
and a value v.1.2 Analyzing algorithms
Analysis of insertion sort


 key in line 5 when i has its initial value of j - 1. Thus tj = 1 for j = 2,3, . . ., n, and the best-case running time is
key in line 5 when i has its initial value of j - 1. Thus tj = 1 for j = 2,3, . . ., n, and the best-case running time isT(n) = c1n + c2 (n - 1) + c4 (n - 1) + c5 (n - 1) + c8 (n - 1)
= (c1 + c2 + c4 + c8)n - (c2 + c4 + c5 + c8).


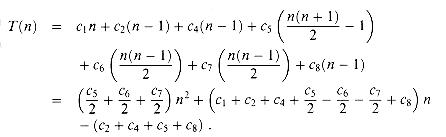
Worst-case and average-case analysis
 The worst-case running time of an algorithm is an upper bound on the running time for any input. Knowing it gives us a guarantee that the algorithm will never take any longer. We need not make some educated guess about the running time and hope that it never gets much worse.
The worst-case running time of an algorithm is an upper bound on the running time for any input. Knowing it gives us a guarantee that the algorithm will never take any longer. We need not make some educated guess about the running time and hope that it never gets much worse. For some algorithms, the worst case occurs fairly often. For example, in searching a database for a particular piece of information, the searching algorithm's worst case will often occur when the information is not present in the database. In some searching applications, searches for absent information may be frequent.
For some algorithms, the worst case occurs fairly often. For example, in searching a database for a particular piece of information, the searching algorithm's worst case will often occur when the information is not present in the database. In some searching applications, searches for absent information may be frequent. The "average case" is often roughly as bad as the worst case. Suppose that we randomly choose n numbers and apply insertion sort. How long does it take to determine where in subarray A[1. . j - 1] to insert element A[j]? On average, half the elements in A[1. . j - 1] are less than A[j], and half the elements are greater. On average, therefore, we check half of the subarray A[1. . j - 1], so tj = j/2. If we work out the resulting average-case running time, it turns out to be a quadratic function of the input size, just like the worst-case running time.
The "average case" is often roughly as bad as the worst case. Suppose that we randomly choose n numbers and apply insertion sort. How long does it take to determine where in subarray A[1. . j - 1] to insert element A[j]? On average, half the elements in A[1. . j - 1] are less than A[j], and half the elements are greater. On average, therefore, we check half of the subarray A[1. . j - 1], so tj = j/2. If we work out the resulting average-case running time, it turns out to be a quadratic function of the input size, just like the worst-case running time.Order of growth
 (n2) (pronounced "theta of n-squared"). We shall use
(n2) (pronounced "theta of n-squared"). We shall use  -notation informally in this chapter; it will be defined precisely in Chapter 2.
-notation informally in this chapter; it will be defined precisely in Chapter 2. (n2) algorithm, for example, will run more quickly in the worst case than a
(n2) algorithm, for example, will run more quickly in the worst case than a  (n3) algorithm.
(n3) algorithm.Exercises
 -notation.
-notation.  -notation? Justify your answers.
-notation? Justify your answers. x1, x2, . . . , xn
x1, x2, . . . , xn of n numbers contains repeated occurrences of some number. Show that this can be done in
of n numbers contains repeated occurrences of some number. Show that this can be done in  (n lg n) time, where lg n stands for log2 n.
(n lg n) time, where lg n stands for log2 n. . Describe a straightforward
. Describe a straightforward  (n2)-time algorithm for this problem. Describe a
(n2)-time algorithm for this problem. Describe a  (n)-time algorithm that uses the following method (called Horner's rule) for rewriting the polynomial:
(n)-time algorithm that uses the following method (called Horner's rule) for rewriting the polynomial:
 -notation.
-notation.1.3 Designing algorithms
1.3.1 The divide-and-conquer approach
 q < r. The procedure assumes that the subarrays A[p. .q] and A[q + 1. .r] are in sorted order. It merges them to form a single sorted subarray that replaces the current subarray A[p. .r].
q < r. The procedure assumes that the subarrays A[p. .q] and A[q + 1. .r] are in sorted order. It merges them to form a single sorted subarray that replaces the current subarray A[p. .r]. (n), where n = r - p + 1 is the number of elements being merged. Returning to our card-playing motif, suppose we have two piles of cards face up on a table. Each pile is sorted, with the smallest cards on top. We wish to merge the two piles into a single sorted output pile, which is to be face down on the table. Our basic step consists of choosing the smaller of the two cards on top of the face-up piles, removing it from its pile (which exposes a new top card), and placing this card face down onto the output pile. We repeat this step until one input pile is empty, at which time we just take the remaining input pile and place it face down onto the output pile. Computationally, each basic step takes constant time, since we are checking just two top cards. Since we perform at most n basic steps, merging takes
(n), where n = r - p + 1 is the number of elements being merged. Returning to our card-playing motif, suppose we have two piles of cards face up on a table. Each pile is sorted, with the smallest cards on top. We wish to merge the two piles into a single sorted output pile, which is to be face down on the table. Our basic step consists of choosing the smaller of the two cards on top of the face-up piles, removing it from its pile (which exposes a new top card), and placing this card face down onto the output pile. We repeat this step until one input pile is empty, at which time we just take the remaining input pile and place it face down onto the output pile. Computationally, each basic step takes constant time, since we are checking just two top cards. Since we perform at most n basic steps, merging takes  (n) time.
(n) time. r, the subarray has at most one element and is therefore already sorted. Otherwise, the divide step simply computes an index q that partitions A[p. .r] into two subarrays: A[p. .q], containing n/2] elements, and A[q + 1. .r], containing
r, the subarray has at most one element and is therefore already sorted. Otherwise, the divide step simply computes an index q that partitions A[p. .r] into two subarrays: A[p. .q], containing n/2] elements, and A[q + 1. .r], containing  n/2
n/2 elements.4
elements.4 x
x denotes the least integer greater than or equal to x, and
denotes the least integer greater than or equal to x, and  x
x denotes the greatest integer less than or equal to x. These notations are defined in Chapter 2.
denotes the greatest integer less than or equal to x. These notations are defined in Chapter 2.MERGE-SORT(A,p,r)
1 if p < r
2 then q

 (p + r)/2
(p + r)/2
3 MERGE-SORT(A,p,q)
4 MERGE-SORT(A, q + 1, r)
5 MERGE(A,p,q,r)
 A[1],A[2], . . . ,A[n]
A[1],A[2], . . . ,A[n] , we call MERGE-SORT(A, 1, length[A]), where once again length[A] = n. If we look at the operation of the procedure bottom-up when n is a power of two, the algorithm consists of merging pairs of 1-item sequences to form sorted sequences of length 2, merging pairs of sequences of length 2 to form sorted sequences of length 4, and so on, until two sequences of length n/2 are merged to form the final sorted sequence of length n. Figure 1.3 illustrates this process.
, we call MERGE-SORT(A, 1, length[A]), where once again length[A] = n. If we look at the operation of the procedure bottom-up when n is a power of two, the algorithm consists of merging pairs of 1-item sequences to form sorted sequences of length 2, merging pairs of sequences of length 2 to form sorted sequences of length 4, and so on, until two sequences of length n/2 are merged to form the final sorted sequence of length n. Figure 1.3 illustrates this process.1.3.2 Analyzing divide-and-conquer algorithms
 c for some constant c, the straightforward solution takes constant time, which we write as
c for some constant c, the straightforward solution takes constant time, which we write as  (1). Suppose we divide the problem into a subproblems, each of which is 1/b the size of the original. If we take D(n) time to divide the problem into subproblems and C(n) time to combine the solutions to the subproblems into the solution to the original problem, we get the recurrence
(1). Suppose we divide the problem into a subproblems, each of which is 1/b the size of the original. If we take D(n) time to divide the problem into subproblems and C(n) time to combine the solutions to the subproblems into the solution to the original problem, we get the recurrence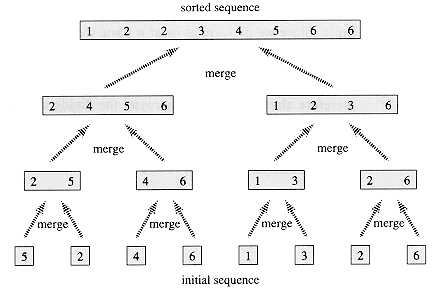
Figure 1.3 The operation of merge sort on the array A =
 5, 2, 4, 6, 1, 3, 2, 6
5, 2, 4, 6, 1, 3, 2, 6 . The lengths of the sorted sequences being merged increase as the algorithm progresses from bottom to top.
. The lengths of the sorted sequences being merged increase as the algorithm progresses from bottom to top.
Analysis of merge sort
 (1).
(1). (n), so C(n) =
(n), so C(n) =  (n).
(n). (n) and a function that is
(n) and a function that is  (1). This sum is a linear function of n, that is,
(1). This sum is a linear function of n, that is,  (n). Adding it to the 2T(n/2) term from the "conquer" step gives the recurrence for the worst-case running time T(n) of merge sort:
(n). Adding it to the 2T(n/2) term from the "conquer" step gives the recurrence for the worst-case running time T(n) of merge sort:
 (n 1g n), where 1g n stands for log2 n. For large enough inputs, merge sort, with its
(n 1g n), where 1g n stands for log2 n. For large enough inputs, merge sort, with its  (n lg n) running time, outperforms insertion sort, whose running time is
(n lg n) running time, outperforms insertion sort, whose running time is  (n2), in the worst case.
(n2), in the worst case.Exercises
 3, 41, 52, 26, 38, 57, 9, 49
3, 41, 52, 26, 38, 57, 9, 49 .
.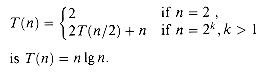
 (lg n).
(lg n). (n lg n)?
(n lg n)? (n lg n)-time algorithm that, given a set S of n real numbers and another real number x, determines whether or not there exist two elements in S whose sum is exactly x.
(n lg n)-time algorithm that, given a set S of n real numbers and another real number x, determines whether or not there exist two elements in S whose sum is exactly x.1.4 Summary

Exercises
Problems
 (n lg n) worst-case time and insertion sort runs in
(n lg n) worst-case time and insertion sort runs in  (n2) worst-case time, the constant factors in insertion sort make it faster for small n. Thus, it makes sense to use insertion sort within merge sort when subproblems become sufficiently small. Consider a modification to merge sort in which n/k sublists of length k are sorted using insertion sort and then merged using the standard merging mechanism, where k is a value to be determined.
(n2) worst-case time, the constant factors in insertion sort make it faster for small n. Thus, it makes sense to use insertion sort within merge sort when subproblems become sufficiently small. Consider a modification to merge sort in which n/k sublists of length k are sorted using insertion sort and then merged using the standard merging mechanism, where k is a value to be determined. (nk) worst-case time.
(nk) worst-case time. (n lg(n/k)) worst-case time.
(n lg(n/k)) worst-case time. (nk + n 1g(n/k)) worst-case time, what is the largest asymptotic (
(nk + n 1g(n/k)) worst-case time, what is the largest asymptotic ( -notation) value of k as a function of n for which the modified algorithm has the same asymptotic running time as standard merge sort?
-notation) value of k as a function of n for which the modified algorithm has the same asymptotic running time as standard merge sort? 2, 3, 8, 6, 1
2, 3, 8, 6, 1 .
. (n 1g n) worst-case time. (Hint: Modify merge sort.)
(n 1g n) worst-case time. (Hint: Modify merge sort.)Chapter notes


