The iteration operator "*" used in the 1g* function can be applied to monotonically increasing functions over the reals. For a function â satisfying f(n) < n, we define the function f(i) recursively for nonnegative integers i by

For a given constant c  R, we define the iterated function
R, we define the iterated function  by
by

which need not be well-defined in all cases. In other words, the quantity  (n) is the number of iterated applications of the function â required to reduce its argument down to c or less.
(n) is the number of iterated applications of the function â required to reduce its argument down to c or less.
For each of the following functions f (n) and constants c, give as tight a bound as possible on  (n).
(n).

Chapter notes
Knuth [121] traces the origin of the O-notation to a number-theory text by P. Bachmann in 1892. The o-notation was invented by E. Landau in 1909 for his discussion of the distribution of prime numbers. The  and
and  notations were advocated by Knuth [124] to correct the popular, but technically sloppy, practice in the literature of using O-notation for both upper and lower bounds. Many people continue to use the O-notation where the
notations were advocated by Knuth [124] to correct the popular, but technically sloppy, practice in the literature of using O-notation for both upper and lower bounds. Many people continue to use the O-notation where the  -notation is more technically precise. Further discussion of the history and development of asymptotic notations can be found in Knuth[121, 124] and Brassard and Bratley [33].
-notation is more technically precise. Further discussion of the history and development of asymptotic notations can be found in Knuth[121, 124] and Brassard and Bratley [33].
Not all authors define the asymptotic notations in the same way, although the various definitions agree in most common situations. Some of the alternative definitions encompass functions that are not asymptotically nonnegative, as long as their absolute values are appropriately bounded.
Other properties of elementary mathematical functions can be found in any good mathematical reference, such as Abramowitz and Stegun [1] or Beyer [27], or in a calculus book, such as Apostol [12] or Thomas and Finney [192]. Knuth [121] contains a wealth of material on discrete mathematics as used in computer science.
Go to Chapter 3 Back to Table of Contents
 (n lg n) worst-case running time, beats insertion sort, whose worst-case running time is
(n lg n) worst-case running time, beats insertion sort, whose worst-case running time is  (n2). Although we can sometimes determine the exact running time of an algorithm, as we did for insertion sort in Chapter 1, the extra precision is not usually worth the effort of computing it. For large enough inputs, the multiplicative constants and lower-order terms of an exact running time are dominated by the effects of the input size itself.
(n2). Although we can sometimes determine the exact running time of an algorithm, as we did for insertion sort in Chapter 1, the extra precision is not usually worth the effort of computing it. For large enough inputs, the multiplicative constants and lower-order terms of an exact running time are dominated by the effects of the input size itself.


 c1g(n)
c1g(n)  n0}.
n0}.


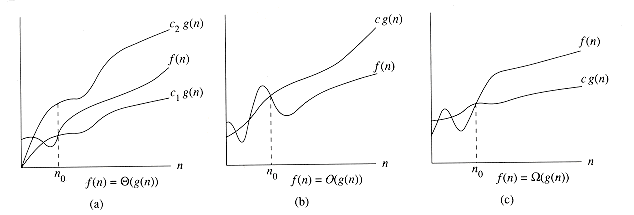
 notations. In each part, the value of n0 shown is the minimum possible value; any greater value would also work. (a)
notations. In each part, the value of n0 shown is the minimum possible value; any greater value would also work. (a)  (n) =
(n) =  . Certainly, other choices for the constants exist, but the important thing is that some choice exists. Note that these constants depend on the function
. Certainly, other choices for the constants exist, but the important thing is that some choice exists. Note that these constants depend on the function  a different function belonging to
a different function belonging to 
 . The reader may verify that 0
. The reader may verify that 0  where the ai are constants and ad > 0, we have p(n) =
where the ai are constants and ad > 0, we have p(n) =  -calculus, the parameters to a function are clearly specified: the function n2 could be written as
-calculus, the parameters to a function are clearly specified: the function n2 could be written as  O(g(n)). Thus, our proof that any quadratic function an2 + bn + c, where a > 0, is in
O(g(n)). Thus, our proof that any quadratic function an2 + bn + c, where a > 0, is in 



 a
a 
 x
x (read "the floor of x") and the least integer greater than or equal to x by
(read "the floor of x") and the least integer greater than or equal to x by  x
x (read "the ceiling of x"). For all real x,
(read "the ceiling of x"). For all real x,


 0, the approximation of ex by 1 + x is quite good:
0, the approximation of ex by 1 + x is quite good: .) We have for all x,
.) We have for all x,
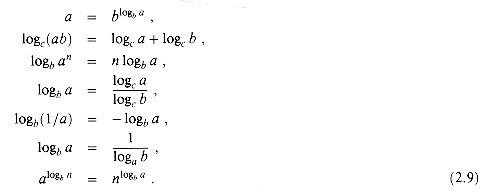
 x
x







 and to its conjugate
and to its conjugate  , which are given by the following formulas:
, which are given by the following formulas:

 < 1, we have
< 1, we have  , so that the ith Fibonacci number Fi is equal to
, so that the ith Fibonacci number Fi is equal to  rounded to the nearest integer. Thus, Fibonacci numbers grow exponentially.
rounded to the nearest integer. Thus, Fibonacci numbers grow exponentially. where
where  is its conjugate.
is its conjugate.
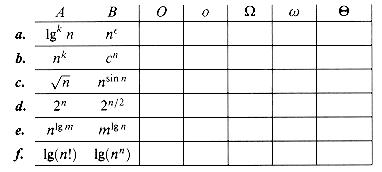
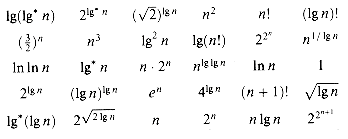
 (read "omega infinity") for this alternative definition. We say that
(read "omega infinity") for this alternative definition. We say that  if there exists a positive constant c such that f(n)
if there exists a positive constant c such that f(n)  (g(n)) or both, whereas this is not true if we use
(g(n)) or both, whereas this is not true if we use 
 instead of
instead of  (read "soft-oh") to mean O with logarithmic factors ignored:
(read "soft-oh") to mean O with logarithmic factors ignored: in a similar manner. Prove the corresponding analog to Theorem 2.1.
in a similar manner. Prove the corresponding analog to Theorem 2.1.
 by
by
 (n) is the number of iterated applications of the function â required to reduce its argument down to c or less.
(n) is the number of iterated applications of the function â required to reduce its argument down to c or less. (n).
(n).