The ith order statistic of a set of n elements is the ith smallest element. For example, the minimum of a set of elements is the first order statistic (i = 1), and the maximum is the nth order statistic (i = n). A median, informally, is the "halfway point" of the set. When n is odd, the median is unique, occurring at i = (n + 1)/2. When n is even, there are two medians, occurring at i = n/2 and i = n/2 + 1. Thus, regardless of the parity of n, medians occur at i =
This chapter addresses the problem of selecting the ith order statistic from a set of n distinct numbers. We assume for convenience that the set contains distinct numbers, although virtually everything that we do extends to the situation in which a set contains repeated values. The selection problem can be specified formally as follows:
Input: A set A of n (distinct) numbers and a number i, with 1
Output: The element x
The selection problem can be solved in O(n lg n) time, since we can sort the numbers using heapsort or merge sort and then simply index the ith element in the output array. There are faster algorithms, however.
In Section 10.1, we examine the problem of selecting the minimum and maximum of a set of elements. More interesting is the general selection problem, which is investigated in the subsequent two sections. Section 10.2 analyzes a practical algorithm that achieves an O(n) bound on the running time in the average case. Section 10.3 contains an algorithm of more theoretical interest that achieves the O(n) running time in the worst case.
How many comparisons are necessary to determine the minimum of a set of n elements? We can easily obtain an upper bound of n - 1 comparisons: examine each element of the set in turn and keep track of the smallest element seen so far. In the following procedure, we assume that the set resides in array A, where length[A] = n.
Finding the maximum can, of course, be accomplished with n - 1 comparisons as well.
Is this the best we can do? Yes, since we can obtain a lower bound of n - 1 comparisons for the problem of determining the minimum. Think of any algorithm that determines the minimum as a tournament among the elements. Each comparison is a match in the tournament in which the smaller of the two elements wins. The key observation is that every element except the winner must lose at least one match. Hence, n - 1 comparisons are necessary to determine the minimum, and the algorithm MINIMUM is optimal with respect to the number of comparisons performed.
An interesting fine point of the analysis is the determination of the expected number of times that line 4 is executed. Problem 6-2 asks you to show that this expectation is
In some applications, we must find both the minimum and the maximum of a set of n elements. For example, a graphics program may need to scale a set of (x, y) data to fit onto a rectangular display screen or other graphical output device. To do so, the program must first determine the minimum and maximum of each coordinate.
It is not too difficult to devise an algorithm that can find both the minimum and the maximum of n elements using the asymptotically optimal
In fact, only 3
10.1-1
Show that the second smallest of n elements can be found with n+
10.1-2
Show that
The general selection problem appears more difficult than the simple problem of finding a minimum, yet, surprisingly, the asymptotic running time for both problems is the same:
RANDOMIZED-SELECT uses the procedure RANDOMIZED-PARTITION introduced in Section 8.3. Thus, like RANDOMIZED-QUICKSORT, it is a randomized algorithm, since its behavior is determined in part by the output of a random-number generator. The following code for RANDOMIZED-SELECT returns the ith smallest element of the array A[p . . r].
After RANDOMIZED-PARTITION is executed in line 3 of the algorithm, the array A[p .. r] is partitioned into two nonempty subarrays A[p .. q] and A[q + 1 .. r] such that each element of A[p .. q] is less than each element of A[q + 1 .. r]. Line 4 of the algorithm computes the number k of elements in the subarray A[p .. q]. The algorithm now determines in which of the two subarrays A[p .. q] and A[q + 1 .. r] the ith smallest element lies. If i
The worst-case running time for RANDOMIZED-SELECT is
We can obtain an upper bound T(n) on the expected time required by RANDOMIZED-SELECT on an input array of n elements as follows. We observed in Section 8.4 that the algorithm RANDOMIZED-PARTITION produces a partition whose low side has 1 element with probability 2/n and i elements with probability 1/n for i = 2, 3, . . . , n - 1. Assuming that T(n) is monotonically increasing, in the worst case RANDOMIZED-SELECT is always unlucky in that the ith element is determined to be on the larger side of the partition. Thus, we get the recurrence
The second line follows from the first since max(1, n - 1 ) = n - 1 and
If n is odd, each term T(
We solve the recurrence by substitution. Assume that T(n)
since we can pick c large enough so that c(n/4 + 1/2) dominates the O(n) term.
Thus, any order statistic, and in particular the median, can be determined on average in linear time.
10.2-1
Write an iterative version of RANDOMIZED-SELECT.
10.2-2
Suppose we use RANDOMIZED-SELECT to select the minimum element of the array A =
10.2-3
Recall that in the presence of equal elements, the RANDOMIZED-PARTITION procedure partitions the subarray A[p . . r] into two nonempty subarrays A[p . . q] and A[q + 1 . . r] such that each element in A[p . . q] is less than or equal to every element in A[q + 1 . . r]. If equal elements are present, does the RANDOMIZED-SELECT procedure work correctly?
We now examine a selection algorithm whose running time is O(n) in the worst case. Like RANDOMIZED-SELECT, the algorithm SELECT finds the desired element by recursively partitioning the input array. The idea behind the algorithm, however, is to guarantee a good split when the array is partitioned. SELECT uses the deterministic partitioning algorithm PARTITION from quicksort (see Section 8.1), modified to take the element to partition around as an input parameter.
The SELECT algorithm determines the ith smallest of an input array of n elements by executing the following steps.
1. Divide the n elements of the input array into
2. Find the median of each of the
3. Use SELECT recursively to find the median x of the
4. Partition the input array around the median-of-medians x using a modified version of PARTITION. Let k be the number of elements on the low side of the partition, so that n - k is the number of elements on the high side.
5. Use SELECT recursively to find the ith smallest element on the low side if i
To analyze the running time of SELECT, we first determine a lower bound on the number of elements that are greater than the partitioning element x. Figure 10.1 is helpful in visualizing this bookkeeping. At least half of the medians found in step 2 are greater than or equal to the median-of-medians x. Thus, at least half of the
Similarly, the number of elements that are less than x is at least 3n/10 - 6. Thus, in the worst case, SELECT is called recursively on at most 7n/10 + 6 elements in step 5.
We can now develop a recurrence for the worst-case running time T(n) of the algorithm SELECT. Steps 1, 2, and 4 take O(n) time. (Step 2 consists of O(n) calls of insertion sort on sets of size O(1).) Step 3 takes time T(
We show that the running time is linear by substitution. Assume that T(n)
since we can pick c large enough so that c(n / 10 - 7) is larger than the function described by the O(n) term for all n > 80. The worst-case running time of SELECT is therefore linear.
As in a comparison sort (see Section 9.1), SELECT and RANDOMIZED-SELECT determine information about the relative order of elements only by comparing elements. Thus, the linear-time behavior is not a result of assumptions about the input, as was the case for the sorting algorithms in Chapter 9. Sorting requires
10.3-1
In the algorithm SELECT, the input elements are divided into groups of 5. Will the algorithm work in linear time if they are divided into groups of 7? How about groups of 3?
10.3-2
Analyze SELECT to show that the number of elements greater than the median-of-medians x and the number of elements less than x is at least
10.3-3
Show how quicksort can be made to run in O(n 1g n) time in the worst case.
10.3-4
Suppose that an algorithm uses only comparisons to find the ith smallest element in a set of n elements. Show that it can also find the i - 1 smaller elements and the n - i larger elements without performing any additional comparisons.
10.3-5
Given a "black-box" worst-case linear-time median subroutine, give a simple, linear-time algorithm that solves the selection problem for an arbitrary order statistic.
10.3-6
The kth quantiles of an n-element set are the k - 1 order statistics that divide the sorted set into k equal-sized sets (to within 1). Give an O(n 1g k)-time algorithm to list the kth quantiles of a set.
10.3-7
Describe an O(n)-time algorithm that, given a set S of n distinct numbers and a positive integer k
10.3-8
Let X[1 . . n] and Y[1 . . n] be two arrays, each containing n numbers already in sorted order. Give an O(1g n)-time algorithm to find the median of all 2n elements in arrays X and Y.
10.3-9
Professor Olay is consulting for an oil company, which is planning a large pipeline running east to west through an oil field of n wells. From each well, a spur pipeline is to be connected directly to the main pipeline along a shortest path (either north or south), as shown in Figure 10.2. Given x- and y-coordinates of the wells, how should the professor pick the optimal location of the main pipeline (the one that minimizes the total length of the spurs)? Show that the optimal location can be determined in linear time.
10-1 Largest i numbers in sorted order
Given a set of n numbers, we wish to find the i largest in sorted order using a comparison-based algorithm. Find the algorithm that implements each of the following methods with the best asymptotic worst-case running time, and analyze the running times of the methods in terms of n and i.
a. Sort the numbers and list the i largest.
b. Build a priority queue from the numbers and call EXTRACT-MAX i times.
c. Use an order-statistic algorithm to find the ith largest number, partition, and sort the i largest numbers.
10-2 Weighted median
For n distinct elements x1, x2, . . . , xn with positive weights w1, w2, . . . , wn such that
a. Argue that the median of x1, x2, . . . , xn is the weighted median of the xi with weights wi = 1 / n for i = 1, 2, . . . , n.
b. Show how to compute the weighted median of n elements in O(n 1g n) worst-case time using sorting.
c. Show how to compute the weighted median in
The post-office location problem is defined as follows. We are given n points p1, p2, . . . , pn with associated weights w1, w2, . . . , wn. We wish to find a point p (not necessarily one of the input points) that minimizes the sum
d. Argue that the weighted median is a best solution for the 1-dimensional post-office location problem, in which points are simply real numbers and the distance between points a and b is d(a, b) = |a - b|.
e. Find the best solution for the 2-dimensional post-office location problem, in which the points are (x, y) coordinate pairs and the distance between points a = (x1, y1) and b = (x2, y2) is the Manhattan distance: d(a, b) = |x1 - x2| + |y1 - y2|.
10-3 Small order statistics
The worst-case number T(n) of comparisons used by SELECT to select the ith order statistic from n numbers was shown to satisfy T(n) =
a. Describe an algorithm that uses Ui(n) comparisons to find the ith smallest of n elements, where i
(Hint: Begin with
b. Show that Ui(n) = n + O(T(2i)1g(n / i)).
c. Show that if i is a constant, then Ui(n) = n + O(1g n).
d. Show that if i = n / k for k
The worst-case median-finding algorithm was invented by Blum, Floyd, Pratt, Rivest, and Tarjan [29]. The fast average-time version is due to Hoare [97]. Floyd and Rivest [70] have developed an improved average-time version that partitions around an element recursively selected from a small sample of the elements.
(n + 1)/2
and i = 
(n + 1)/2
.
i n.
A that is larger than exactly i -1 other elements of A.10.1 Minimum and maximum
MINIMUM (A)
1 min
A[1]2 for i
2 to length[A]3 do if min > A[i]
4 then min
A[i]5 return min
(lg n).Simultaneous minimum and maximum
(n) number of comparisons. Simply find the minimum and maximum independently, using n - 1 comparisons for each, for a total of 2n - 2 comparisons.n/2 comparisons are necessary to find both the minimum and the maximum. To do this, we maintain the minimum and maximum elements seen thus far. Rather than processing each element of the input by comparing it against the current minimum and maximum, however, at a cost of two comparisons per element, we process elements in pairs. We compare pairs of elements from the input first with each other, and then compare the smaller to the current minimum and the larger to the current maximum, at a cost of three comparisons for every two elements.Exercises
lg n - 2 comparisons in the worst case. (Hint: Also find the smallest element.)3n/2 - 2 comparisons are necessary in the worst case to find both the maximum and minimum of n numbers. (Hint: Consider how many numbers are potentially either the maximum or minimum, and investigate how a comparison affects these counts.)10.2 Selection in expected linear time
(n). In this section, we present a divide-and-conquer algorithm for the selection problem. The algorithm RANDOMIZED-SELECT is modeled after the quicksort algorithm of Chapter 8. As in quicksort, the idea is to partition the input array recursively. But unlike quicksort, which recursively processes both sides of the partition, RANDOMIZED-SELECT only works on one side of the partition. This difference shows up in the analysis: whereas quicksort has an expected running time of (n lg n), the expected time of RANDOMIZED-SELECT is (n).RANDOMIZED-SELECT(A, p, r, i)
1 if p = r
2 then return A[p]
3 q
RANDOMIZED-PARTITION(A, p, r)4 k
q - p + 15 if i
k6 then return RANDOMIZED-SELECT(A, p, q, i)
7 else return RANDOMIZED-SELECT(A, q + 1, r, i - k)
k, then the desired element lies on the low side of the partition, and it is recursively selected from the subarray in line 6. If i > k, however, then the desired element lies on the high side of the partition. Since we already know k values that are smaller than the ith smallest element of A[p .. r]--namely, the elements of A[p .. q]--the desired element is the (i - k)th smallest element of A[q + 1 .. r], which is found recursively in line 7.(n2), even to find the minimum, because we could be extremely unlucky and always partition around the largest remaining element. The algorithm works well in the average case, though, and because it is randomized, no particular input elicits the worst-case behavior.
n/2), T(n/2 + 1), . . . ,T(n - 1) appears twice in the summation, and if n is even, each term T(n/2 + 1), T(n/2 + 2), . . . , T(n - 1) appears twice and the term T(n/2) appears once. In either case, the summation of the first line is bounded from above by the summation of the second line. The third line follows from the second since in the worst case T(n - 1) = O(n2), and thus the term 
can be absorbed by the term O(n). cn for some constant c that satisfies the initial conditions of the recurrence. Using this inductive hypothesis, we have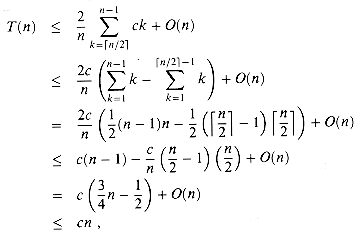
Exercises
3, 2, 9, 0, 7, 5, 4, 8, 6, 1
. Describe a sequence of partitions that results in a worst-case performance of RANDOMIZED-SELECT.10.3 Selection in worst-case linear time
Figure 10.1 Analysis of the algorithm SELECT. The n elements are represented by small circles, and each group occupies a column. The medians of the groups are whitened, and the median-of-medians x is labeled. Arrows are drawn from larger elements to smaller, from which it can be seen that 3 out of every group of 5 elements to the right of x are greater than x, and 3 out of every group of 5 elements to the left of x are less than x. The elements greater than x are shown on a shaded background.
n/5 groups of 5 elements each and at most one group made up of the remaining n mod 5 elements.n/5 groups by insertion sorting the elements of each group (of which there are 5 at most) and taking its middle element. (If the group has an even number of elements, take the larger of the two medians.)n/5 medians found in step 2. k, or the (i - k)th smallest element on the high side if i > k.n/5 groups contribute 3 elements that are greater than x, except for the one group that has fewer than 5 elements if 5 does not divide n exactly, and the one group containing x itself. Discounting these two groups, it follows that the number of elements greater than x is at least
n/5), and step 5 takes time at most T(7n / 10 + 6), assuming that T is monotonically increasing. Note that 7n / 10 + 6 < n for n > 20 and that any input of 80 or fewer elements requires O(1) time. We can therefore obtain the recurrence
cn for some constant c and all n 80. Substituting this inductive hypothesis into the right-hand side of the recurrence yieldsT(n)
c n/5 + c(7n/10 + 6) + O(n) cn/5 + c + 7cn/10 + 6c + O(n) 9cn/10 + 7c + O(n) cn,(n 1g n) time in the comparison model, even on average (see Problem 9-1), and thus the method of sorting and indexing presented in the introduction to this chapter is asymptotically inefficient.Exercises
n/4 if n 
38. n, determines the k numbers in S that are closest to the median of S.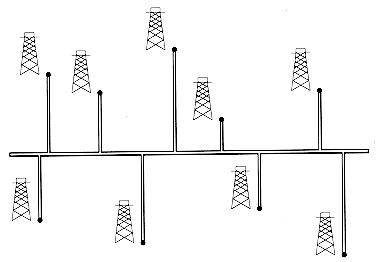
Figure 10.2 We want to determine the position of the east-west oil pipeline that minimizes the total length of the north-south spurs.
Problems
the weighted median is the element xk satisfying
(n) worst-case time using a linear-time median algorithm such as SELECT from Section 10.3.
, where d(a, b) is the distance between points a and b. (n), but the constant hidden by the -notation is rather large. When i is small relative to n, we can implement a different procedure that uses SELECT as a subroutine but makes fewer comparisons in the worst case. n / 2 and
n / 2 disjoint pairwise comparisons, and recurse on the set containing the smaller element from each pair.) 2, then Ui(n) = n + O(T(2n / k) 1g k).Chapter notes