Greedy algorithms do not always yield optimal solutions, but for many problems they do. We shall first examine in Section 17.1 a simple but nontrivial problem, the activity-selection problem, for which a greedy algorithm efficiently computes a solution. Next, Section 17.2 reviews some of the basic elements of the greedy approach. Section 17.3 presents an important application of greedy techniques: the design of data-compression (Huffman) codes. In Section 17.4, we investigate some of the theory underlying combinatorial structures called "matroids" for which a greedy algorithm always produces an optimal solution. Finally, Section 17.5 illustrates the application of matroids using the problem of scheduling unit-time tasks with deadlines and penalties.
The greedy method is quite powerful and works well for a wide range of problems. Later chapters will present many algorithms that can be viewed as applications of the greedy method, including minimum-spanning-tree algorithms (Chapter 24), Dijkstra's algorithm for shortest paths form a single source (Chapter 25), and Chvátal's greedy set-covering heuristic (Chapter 37). Minimum spanning trees form a classic example of the greedy method. Although this chapter and Chapter 24 can be read independently of each other, you may find it useful to read them together.
17.1 An activity-selection problem
Our first example is the problem of scheduling a resource among several competing activities. We shall find that a greedy algorithm provides an elegant and simple method for selecting a maximum-size set of mutually compatible activities.
Suppose we have a set S = { 1, 2, . . . , n} of n proposed activities that wish to use a resource, such as a lecture hall, which can be used by only one activity at a time. Each activity i has a start time si and a finish time âi, where si
A greedy algorithm for the activity-selection problem is given in the following pseudocode. We assume that the input activities are in order by increasing finishing time:
If not, we can sort them into this order in time O(n 1g n), breaking ties arbitrarily. The pseudocode assumes that inputs s and â are represented as arrays.
The operation of the algorithm is shown in Figure 17.1. The set A collects the selected activities. The variable j specifies the most recent addition to A. Since the activities are considered in order of nondecreasing finishing time, fj is always the maximum finishing time of any activity in A. That is,
Lines 2-3 select activity 1, initialize A to contain just this activity, and initialize j to this activity. Lines 4-7 consider each activity i in turn and add i to A if it is compatible with all previously selected activities. To see if activity i is compatible with every activity currently in A, it suffices by equation (17.2) to check (line 5) that its start time si is not earlier than the finish time fj of the activity most recently added to A. If activity i is compatible, then lines 6-7 add it to A and update j. The GREEDY-ACTIVITY-SELECTOR procedure is quite efficient. It can schedule a set S of n activities in
The activity picked next by GREEDY-ACTIVITY-SELECTOR is always the one with the earliest finish time that can be legally seheduled. The activity picked is thus a "greedy" choice in the sense that, intuitively, it leaves as much opportunity as possible for the remaining activities to be scheduled. That is, the greedy choice is the one that maximizes the amount of unscheduled time remaining.
Greedy algorithms do not always produce optimal solutions. However, GREEDY-ACTIVITY-SELECTOR always finds an optimal solution to an instance of the activity-selection problem.
Theorem 17.1
Algorithm GREEDY-ACTIVITY-SELECTOR produces solutions of maximum size for the activity-selection problem.
Proof Let S = {1, 2, . . . , n} be the set of activities to schedule. Since we are assuming that the activities are in order by finish time, activity 1 has the earliest finish time. We wish to show that there is an optimal solution that begins with a greedy choice, that is, with activity 1.
Suppose that A
Moreover, once the greedy choice of activity 1 is made, the problem reduces to finding an optimal solution for the activity-selection problem over those activities in S that are compatible with activity 1. That is, if A is an optimal solution to the original problem S, then A' = A - {1} is an optimal solution to the activity-selection problem S' = {i
17.1-1
Give a dynamic-programming algorithm for the activity-selection problem, based on computing mi iteratively for i = 1, 2, . . . , n, where mi is the size of the largest set of mutually compatible activities among activities {1, 2, . . . , i}. Assume that the inputs have been sorted as in equation (17.1). Compare the running time of your solution to the running time of GREEDY-ACTIVITY-SELECTOR.
17.1-2
Suppose that we have a set of activities to schedule among a large number of lecture halls. We wish to schedule all the activities using as few lecture halls as possible. Give an efficient greedy algorithm to determine which activity should use which lecture hall.
(This is also known as the interval-graph coloring problem. We can create an interval graph whose vertices are the given activities and whose edges connect incompatible activities. The smallest number of colors required to color every vertex so that no two adjacent vertices are given the same color corresponds to finding the fewest lecture halls needed to schedule all of the given activities.)
17.1-3
Not just any greedy approach to the activity-selection problem produces a maximum-size set of mutually compatible activities. Give an example to show that the approach of selecting the activity of least duration from those that are compatible with previously selected activities does not work. Do the same for the approach of always selecting the activity that overlaps the fewest other remaining activities.
A greedy algorithm obtains an optimal solution to a problem by making a sequence of choices. For each decision point in the algorithm, the choice that seems best at the moment is chosen. This heuristic strategy does not always produce an optimal solution, but as we saw in the activity-selection problem, sometimes it does. This section discusses some of the general properties of greedy methods.
How can one tell if a greedy algorithm will solve a particular optimization problem? There is no way in general, but there are two ingredients that are exhibited by most problems that lend themselves to a greedy strategy: the greedy-choice property and optimal substructure.
The first key ingredient is the greedy-choice property: a globally optimal solution can be arrived at by making a locally optimal (greedy) choice. Here is where greedy algorithms differ from dynamic programming. In dynamic programming, we make a choice at each step, but the choice may depend on the solutions to subproblems. In a greedy algorithm, we make whatever choice seems best at the moment and then solve the subproblems arising after the choice is made. The choice made by a greedy algorithm may depend on choices so far, but it cannot depend on any future choices or on the solutions to subproblems. Thus, unlike dynamic programming, which solves the subproblems bottom up, a greedy strategy usually progresses in a top-down fashion, making one greedy choice after another, iteratively reducing each given problem instance to a smaller one.
Of course, we must prove that a greedy choice at each step yields a globally optimal solution, and this is where cleverness may be required. Typically, as in the case of Theorem 17.1, the proof examines a globally optimal solution. It then shows that the solution can be modified so that a greedy choice is made as the first step, and that this choice reduces the problem to a similar but smaller problem. Then, induction is applied to show that a greedy choice can be used at every step. Showing that a greedy choice results in a similar but smaller problem reduces the proof of correctness to demonstrating that an optimal solution must exhibit optimal substructure.
A problem exhibits optimal substructure if an optimal solution to the problem contains within it optimal solutions to subproblems. This property is a key ingredient of assessing the applicability of dynamic programming as well as greedy algorithms. As an example of optimal substructure, recall that the proof of Theorem 17.1 demonstrated that if an optimal solution A to the activity selection problem begins with activity 1, then the set of activities A' = A - {1} is an optimal solution to the activity-selection problem S' = {i
Because the optimal-substructure property is exploited by both greedy and dynamic-programming strategies, one might be tempted to generate a dynamic-programming solution to a problem when a greedy solution suffices, or one might mistakenly think that a greedy solution works when in fact a dynamic-programming solution is required. To illustrate the subtleties between the two techniques, let us investigate two variants of a classical optimization problem.
The 0-1 knapsack problem is posed as follows. A thief robbing a store finds n items; the ith item is worth vi dollars and weighs wi pounds, where vi and wi are integers. He wants to take as valuable a load as possible, but he can carry at most W pounds in his knapsack for some integer W. What items should he take? (This is called the 0-1 knapsack problem because each item must either be taken or left behind; the thief cannot take a fractional amount of an item or take an item more than once.)
In the fractional knapsack problem, the setup is the same, but the thief can take fractions of items, rather than having to make a binary (0-1) choice for each item. You can think of an item in the 0-1 knapsack problem as being like a gold ingot, while an item in the fractional knapsack problem is more like gold dust.
Both knapsack problems exhibit the optimal-substructure property. For the 0-1 problem, consider the most valuable load that weighs at most W pounds. If we remove item j from this load, the remaining load must be the most valuable load weighing at most W - wj that the thief can take from the n - 1 original items excluding j. For the comparable fractional problem, consider that if we remove a weight w of one item j from the optimal load, the remaining load must be the most valuable load weighing at most W - w that the thief can take from the n - 1 original items plus wj - w pounds of item j.
Although the problems are similar, the fractional knapsack problem is solvable by a greedy strategy, whereas the 0-1 problem is not. To solve the fractional problem, we first compute the value per pound vi/wi for each item. Obeying a greedy strategy, the thief begins by taking as much as possible of the item with the greatest value per pound. If the supply of that item is exhausted and he can still carry more, he takes as much as possible of the item with the next greatest value per pound, and so forth until he can't carry any more. Thus, by sorting the items by value per pound, the greedy algorithm runs in O(n1gn) time. The proof that the fractional knapsack problem has the greedy-choice property is left as Exercise 17.2-1.
To see that this greedy strategy does not work for the 0-1 knapsack problem, consider the problem instance illustrated in Figure 17.2(a). There are 3 items, and the knapsack can hold 50 pounds. Item 1 weighs 10 pounds and is worth 60 dollars. Item 2 weighs 20 pounds and is worth 100 dollars. Item 3 weighs 30 pounds and is worth 120 dollars. Thus, the value per pound of item 1 is 6 dollars per pound, which is greater than the value per pound of either item 2 (5 dollars per pound) or item 3 (4 dollars per pound). The greedy strategy, therefore, would take item 1 first. As can be seen from the case analysis in Figure 17.2(b), however, the optimal solution takes items 2 and 3, leaving 1 behind. The two possible solutions that involve item 1 are both suboptimal.
For the comparable fractional problem, however, the greedy strategy, which takes item 1 first, does yield an optimal solution, as shown in Figure 17.2 (c). Taking item 1 doesn't work in the 0-1 problem because the thief is unable to fill his knapsack to capacity, and the empty space lowers the effective value per pound of his load. In the 0-1 problem, when we consider an item for inclusion in the knapsack, we must compare the solution to the subproblem in which the item is included with the solution to the subproblem in which the item is excluded before we can make the choice. The problem formulated in this way gives rise to many overlapping subproblems--a hallmark of dynamic programming, and indeed, dynamic programming can be used to solve the 0-1 problem. (See Exercise 17.2-2.)
17.2-1
Prove that the fractional knapsack problem has the greedy-choice property.
17.2-2
Give a dynamic-programming solution to the 0-1 knapsack problem that runs in O(n W) time, where n is number of items and W is the maximum weight of items that the thief can put in his knapsack.
17.2-3
Suppose that in a 0-1 knapsack problem, the order of the items when sorted by increasing weight is the same as their order when sorted by decreasing value. Give an efficient algorithm to find an optimal solution to this variant of the knapsack problem, and argue that your algorithm is correct.
17.2-4
Professor Midas drives an automobile from Newark to Reno along Interstate 80. His car's gas tank, when full, holds enough gas to travel n miles, and his map gives the distances between gas stations on his route. The professor wishes to make as few gas stops as possible along the way. Give an efficient method by which Professor Midas can determine at which gas stations he should stop, and prove that your strategy yields an optimal solution.
17.2-5
Describe an efficient algorithm that, given a set {x1,x2, . . ., xn} of points on the real line, determines the smallest set of unit-length closed intervals that contains all of the given points. Argue that your algorithm is correct.
17.2-6
Show how to solve the fractional knapsack problem in O(n) time. Assume that you have a solution to Problem 10-2.
Huffman codes are a widely used and very effective technique for compressing data; savings of 20% to 90% are typical, depending on the characteristics of the file being compressed. Huffman's greedy algorithm uses a table of the frequencies of occurrence of each character to build up an optimal way of representing each character as a binary string.
Suppose we have a 100,000-character data file that we wish to store compactly. We observe that the characters in the file occur with the frequencies given by Figure 17.3. That is, only six different characters appear, and the character a occurs 45,000 times.
There are many ways to represent such a file of information. We consider the problem of designing a binary character code (or code for short) wherein each character is represented by a unique binary string. If we use a fixed-length code, we need 3 bits to represent six characters: a = 000, b = 001, . . . , f = 101. This method requires 300,000 bits to code the entire file. Can we do better?
A variable-length code can do considerably better than a fixed-length code, by giving frequent characters short codewords and infrequent characters long codewords. Figure 17.3 shows such a code; here the 1-bit string 0 represents a, and the 4-bit string 1100 represents f. This code requires (45
We consider here only codes in which no codeword is also a prefix of some other codeword. Such codes are called prefix codes.1 It is possible to show (although we won't do so here) that the optimal data compression achievable by a character code can always be achieved with a prefix code, so there is no loss of generality in restricting attention to prefix codes.
1 Perhaps "prefix-free codes" would be a better name, but the term "prefix codes" is standard in the literature.
Prefix codes are desirable because they simplify encoding (compression) and decoding. Encoding is always simple for any binary character code; we just concatenate the codewords representing each character of the file. For example, with the variable-length prefix code of Figure 17.3, we code the 3-character file abc as 0
Decoding is also quite simple with a prefix code. Since no codeword is a prefix of any other, the codeword that begins an encoded file is unambiguous. We can simply identify the initial codeword, translate it back to the original character, remove it from the encoded file, and repeat the decoding process on the remainder of the encoded file. In our example, the string 001011101 parses uniquely as 0
The decoding process needs a convenient representation for the prefix code so that the initial codeword can be easily picked off. A binary tree whose leaves are the given characters provides one such representation. We interpret the binary codeword for a character as the path from the root to that character, where 0 means "go to the left child" and 1 means "go to the right child." Figure 17.4 shows the trees for the two codes of our example. Note that these are not binary search trees, since the leaves need not appear in sorted order and internal nodes do not contain character keys.
An optimal code for a file is always represented by a full binary tree, in which every nonleaf node has two children (see Exercise 17.3-1). The fixed-length code in our example is not optimal since its tree, shown in Figure 17.4(a), is not a full binary tree: there are codewords beginning 10 . . . , but none beginning 11 . . . . Since we can now restrict our attention to full binary trees, we can say that if C is the alphabet from which the characters are drawn, then the tree for an optimal prefix code has exactly |C| leaves, one for each letter of the alphabet, and exactly |C| - 1 internal nodes.
Given a tree T corresponding to a prefix code, it is a simple matter to compute the number of bits required to encode a file. For each character c in the alphabet C, let f(c) denote the frequency of c in the file and let dT(c) denote the depth of c's leaf in the tree. Note that dT(c) is also the length of the codeword for character c. The number of bits required to encode a file is thus
which we define as the cost of the tree T.
Huffman invented a greedy algorithm that constructs an optimal prefix code called a Huffman code. The algorithm builds the tree T corresponding to the optimal code in a bottom-up manner. It begins with a set of |C| leaves and performs a sequence of |C| - 1 "merging" operations to create the final tree.
In the pseudocode that follows, we assume that C is a set of n characters and that each character c
For our example, Huffman's algorithm proceeds as shown in Figure 17.5. Since there are 6 letters in the alphabet, the initial queue size is n = 6, and 5 merge steps are required to build the tree. The final tree represents the optimal prefix code. The codeword for a letter is the sequence of edge labels on the path from the root to the letter.
Line 2 initializes the priority queue Q with the characters in C. The for loop in lines 3-8 repeatedly extracts the two nodes x and y of lowest frequency from the queue, and replaces them in the queue with a new node z representing their merger. The frequency of z is computed as the sum of the frequencies of x and y in line 7. The node z has x as its left child and y as its right child. (This order is arbitrary; switching the left and right child of any node yields a different code of the same cost.) After n - 1 mergers, the one node left in the queue--the root of the code tree--is returned in line 9.
The analysis of the running time of Huffman's algorithm assumes that Q is implemented as a binary heap (see Chapter 7). For a set C of n characters, the initialization of Q in line 2 can be performed in O(n) time using the BUILD-HEAP procedure in Section 7.3. The for loop in lines 3-8 is executed exactly |n| - 1 times, and since each heap operation requires time O(1g n), the loop contributes O(n 1g n) to the running time. Thus, the total running time of HUFFMAN on a set of n characters is O(n 1g n).
To prove that the greedy algorithm HUFFMAN is correct, we show that the problem of determining an optimal prefix code exhibits the greedy-choice and optimal-substructure properties. The next lemma shows that the greedy-choice property holds.
Lemma 17.2
Let C be an alphabet in which each character c
Proof The idea of the proof is to take the tree T representing an arbitrary optimal prefix code and modify it to make a tree representing another optimal prefix code such that the characters x and y appear as sibling leaves of maximum depth in the new tree. If we can do this, then their codewords will have the same length and differ only in the last bit.
Let b and c be two characters that are sibling leaves of maximum depth in T. Without loss of generality, we assume that f[b]
because both f[b] - f[x] and dT[b] - dT[x] are nonnegative. More specifically, f[b] - f[x] is nonnegative because x is a minimum-frequency leaf, and dT[b] - dT[x] is nonnegative because b is a leaf of maximum depth in T. Similarly, because exchanging y and c does not increase the cost, B(T') - B(T\") is nonnegative. Therefore, B(T\")
Lemma 17.2 implies that the process of building up an optimal tree by mergers can, without loss of generality, begin with the greedy choice of merging together those two characters of lowest frequency. Why is this a greedy choice? We can view the cost of a single merger as being the sum of the frequencies of the two items being merged. Exercise 17.3-3 shows that the total cost of the tree constructed is the sum of the costs of its mergers. Of all possible mergers at each step, HUFFMAN chooses the one that incurs the least cost.
The next lemma shows that the problem of constructing optimal prefix codes has the optimal-substructure property.
Lemma 17.3
Let T be a full binary tree representing an optimal prefix code over an alphabet C, where frequency f [c] is defined for each character c
Proof We first show that the cost B(T) of tree T can be expressed in terms of the cost B(T') of tree T' by considering the component costs in equation (17.3). For each c
from which we conclude that
If T' represents a nonoptimal prefix code for the alphabet C', then there exists a tree T\" whose leaves are characters in C' such that B(T\") < B(T'). Since z is treated as a character in C', it appears as a leaf in T\". If we add x and y as children of z in T\", then we obtain a prefix code for C with cost B(T\") + f[x] + f[y] < B(T), contradicting the optimality of T. Thus, T' must be optimal for the alphabet C'.
Theorem 17.4
Procedure HUFFMAN produces an optimal prefix code.
Proof Immediate from Lemmas 17.2 and 17.3.
17.3-1
Prove that a binary tree that is not full cannot correspond to an optimal prefix code.
17.3-2
What is an optimal Huffman code for the following set of frequencies, based on the first 8 Fibonacci numbers?
Can you generalize your answer to find the optimal code when the frequencies are the first n Fibonacci numbers?
17.3-3
Prove the total cost of a tree for a code can also be computed as the sum, over all internal nodes, of the combined frequencies of the two children of the node.
17.3-4
Prove that for an optimal code, if the characters are ordered so that their frequencies are nonincreasing, then their codeword lengths are nondecreasing.
17.3-5
Let C = {0, 1, . . . , n - 1} be a set of characters. Show that any optimal prefix code on C can be represented by a sequence of
bits. (Hint: Use 2n- 1 bits to specify the structure of the tree, as discovered by a walk of the tree.)
17.3-6
Generalize Huffman's algorithm to ternary codewords (i.e., codewords using the symbols 0, 1, and 2), and prove that it yields optimal ternary codes.
17.3-7
Suppose a data file contains a sequence of 8-bit characters such that all 256 characters are about as common: the maximum character frequency is less than twice the minimum character frequency. Prove that Huffman coding in this case is no more efficient than using an ordinary 8-bit fixed-length code.
17.3-8
Show that no compression scheme can expect to compress a file of randomly chosen 8-bit characters by even a single bit. (Hint: Compare the number of files with the number of possible encoded files.)
There is a beautiful theory about greedy algorithms, which we sketch in this section. This theory is useful in determining when the greedy method yields optimal solutions. It involves combinatorial structures known as "matroids." Although this theory does not cover all cases for which a greedy method applies (for example, it does not cover the activity-selection problem of Section 17.1 or the Huffman coding problem of Section 17.3), it does cover many cases of practical interest. Furthermore, this theory is being rapidly developed and extended to cover many more applications; see the notes at the end of this chapter for references.
A matroid is an ordered pair
1. S is a finite nonempty set.
2.
3. If
The word "matroid" is due to Hassler Whitney. He was studying matric matroids, in which the elements of S are the rows of a given matrix and a set of rows is independent if they are linearly independent in the usual sense. It is easy to show that this structure defines a matroid (see Exercise 17.4-2).
As another illustration of matroids, consider the graphic matroid
The graphic matroid MG is closely related to the minimum-spanning-tree problem, which is covered in detail in Chapter 24.
Theorem 17.5
If G is an undirected graph, then
Proof Clearly, SG = E is a finite set. Furthermore,
Thus, it remains to show that MG satisfies the exchange property. Suppose that A and B are forests of G and that |B| > |A|. That is, A and B are acyclic sets of edges, and B contains more edges than A does.
It follows from Theorem 5.2 that a forest having k edges contains exactly |V|-k trees. (To prove this another way, begin with |V| trees and no edges. Then, each edge that is added to the forest reduces the number of trees by one.) Thus, forest A contains |V| - |A| trees, and forest B contains |V| - |B| trees.
Since forest B has fewer trees than forest A does, forest B must contain some tree T whose vertices are in two different trees in forest A. Moreover, since T is connected, it must contain an edge (u, v) such that vertices u and v are in different trees in forest A. Since the edge (u, v) connects vertices in two different trees in forest A, the edge (u, v) can be added to forest A without creating a cycle. Therefore, MG satisfies the exchange property, completing the proof that MG is a matroid.
Given a matroid
If A is an independent subset in a matroid M, we say that A is maximal if it has no extensions. That is, A is maximal if it is not contained in any larger independent subset of M. The following property is often useful.
Theorem 17.6
All maximal independent subsets in a matroid have the same size.
Proof Suppose to the contrary that A is a maximal independent subset of M and there exists another larger maximal independent subset B of M. Then, the exchange property implies that A is extendable to a larger independent set A
As an illustration of this theorem, consider a graphic matroid MG for a connected, undirected graph G. Every maximal independent subset of MG must be a free tree with exactly |V| - 1 edges that connects all the vertices of G. Such a tree is called a spanning tree of G.
We say that a matroid
for any A
Many problems for which a greedy approach provides optimal solutions can be formulated in terms of finding a maximum-weight independent subset in a weighted matroid. That is, we are given a weighted matroid
For example, in the minimum-spanning-tree problem, we are given a connected undirected graph G = (V, E) and a length function w such that w (e) is the (positive) length of edge e. (We use the term "length" here to refer to the original edge weights for the graph, reserving the term "weight" to refer to the weights in the associated matroid.) We are asked to find a subset of the edges that connects all of the vertices together and has minimum total length. To view this as a problem of finding an optimal subset of a matroid, consider the weighted matroid MG with weight function w', where w'(e) = w0 - w(e) and w0 is larger than the maximum length of any edge. In this weighted matroid, all weights are positive and an optimal subset is a spanning tree of minimum total length in the original graph. More specifically, each maximal independent subset A corresponds to a spanning tree, and since
for any maximal independent subset A, the independent subset that maximizes w'(A) must minimize w(A). Thus, any algorithm that can find an optimal subset A in an arbitrary matroid can solve the minimum-spanning-tree problem.
Chapter 24 gives algorithms for the minimum-spanning-tree problem, but here we give a greedy algorithm that works for any weighted matroid. The algorithm takes as input a weighted matroid
The elements of S are considered in turn, in order of nonincreasing weight. If the element x being considered can be added to A while maintaining A's independence, it is. Otherwise, x is discarded. Since the empty set is independent by the definition of a matroid, and since x is only added to A if A
The running time of GREEDY is easy to analyze. Let n denote |S|. The sorting phase of GREEDY takes time O(n lg n). Line 4 is executed exactly n times, once for each element of S. Each execution of line 4 requires a check on whether or not the set A
We now prove that GREEDY returns an optima1 subset.
Lemma 17.7
Suppose that
Proof If no such x exists, then the only independent subset is the empty set and we're done. Otherwise, let B be any nonempty optimal subset. Assume that x
No element of B has weight greater than w(x). To see this, observe that y
Construct the set A as follows. Begin with A = {x}. By the choice of x, A is independent. Using the exchange property, repeatedly find a new element of B that can be added to A until |A| = |B| while preserving the independence of A. Then, A = B - {y}
Because B is optimal, A must also be optimal, and because x
We next show that if an element is not an option initially, then it cannot be an option later.
Lemma 17.8
Let
Proof The proof is by contradiction. Assume that x is an extension of A but not of
Lemma 17.8 says that any element that cannot be used immediately can never be used. Therefore, GREEDY cannot make an error by passing over any initial elements in S that are not an extension of
Lemma 17.9
Let x be the first element of S chosen by GREEDY for the weighted matroid
the weight function for M' is the weight function for M, restricted to S'. (We call M' the contraction of M by the element x.)
Proof If A is any maximum-weight independent subset of M containing x, then A' = A - {x} is an independent subset of M'. Conversely, any independent subset A' of M' yields an independent subset A = A'
Theorem 17.10
If
Proof By Lemma 17.8, any elements that are passed over initially because they are not extensions of
17.4-1
Show that
17.4-2
Given an n
17.4-3
Show that if
17.4-4
Let S be a finite set and let S1, S2, . . . , Sk be a partition of S into nonempty disjoint subsets. Define the structure
17.4-5
Show how to transform the weight function of a weighted matroid problem, where the desired optimal solution is a minimum-weight maximal independent subset, to make it an standard weighted-matroid problem. Argue carefully that your transformation is correct.
An interesting problem that can be solved using matroids is the problem of optimally scheduling unit-time tasks on a single processor, where each task has a deadline and a penalty that must be paid if the deadline is missed. The problem looks complicated, but it can be solved in a surprisingly simple manner using a greedy algorithm.
A unit-time task is a job, such as a program to be run on a computer, that requires exactly one unit of time to complete. Given a finite set S of unit-time tasks, a schedule for S is a permutation of S specifying the order in which these tasks are to be performed. The first task in the schedule begins at time 0 and finishes at time 1, the second task begins at time 1 and finishes at time 2, and so on.
The problem of scheduling unit-time tasks with deadlines and penalties for a single processor has the following inputs:
We are asked to find a schedule for S that minimizes the total penalty incurred for missed deadlines.
Consider a given schedule. We say that a task is late in this schedule if it finishes after its deadline. Otherwise, the task is early in the schedule. An arbitrary schedule can always be put into early-first form, in which the early tasks precede the late tasks. To see this, note that if some early task x follows some late task y, then we can switch the positions of x and y without affecting x being early or y being late.
We similarly claim that an arbitrary schedule can always be put into canonical form, in which the early tasks precede the late tasks and the early tasks are scheduled in order of nondecreasing deadlines. To do so, we put the schedule into early-first form. Then, as long as there are two early tasks i and j finishing at respective times k and k + 1 in the schedule such that dj < di, we swap the positions of i and j. Since task j is early before the swap, k + 1
The search for an optimal schedule thus reduces to finding a set A of tasks that are to be early in the optimal schedule. Once A is determined, we can create the actual schedule by listing the elements of A in order of nondecreasing deadline, then listing the late tasks (i.e., S - A) in any order, producing a canonical ordering of the optimal schedule.
We say that a set A of tasks is independent if there exists a schedule for these tasks such that no tasks are late. Clearly, the set of early tasks for a schedule forms an independent set of tasks. Let
Consider the problem of determining whether a given set A of tasks is independent. For t = 1, 2, . . . , n, let Nt(A) denote the number of tasks in A whose deadline is t or earlier.
Lemma 17.11
For any set of tasks A, the following statements are equivalent.
1. The set A is independent.
2. For t = 1, 2, . . . , n, we have Nt(A)
3. If the tasks in A are scheduled in order of nondecreasing deadlines, then no task is late.
Proof Clearly, if Nt(A) > t for some t, then there is no way to make a schedule with no late tasks for set A, because there are more than t tasks to finish before time t. Therefore, (1) implies (2). If (2) holds, then (3) must follow: there is no way to "get stuck" when scheduling the tasks in order of nondecreasing deadlines, since (2) implies that the ith largest deadline is at most i. Finally, (3) trivially implies (1).
Using property 2 of Lemma 17.11, we can easily compute whether or not a given set of tasks is independent (see Exercise 17.5-2).
The problem of minimizing the sum of the penalties of the late tasks is the same as the problem of maximizing the sum of the penalties of the early tasks. The following theorem thus ensures that we can use the greedy algorithm to find an independent set A of tasks with the maximum total penalty.
Theorem 17.12
If S is a set of unit-time tasks with deadlines, and
Proof Every subset of an independent set of tasks is certainly independent. To prove the exchange property, suppose that B and A are independent sets of tasks and that |B| > |A|. Let k be the largest t such that Nt(B)
We now show that A' must be independent by using property 2 of Lemma 17.11. For 1
By Theorem 17.10, we can use a greedy algorithm to find a maximum- weight independent set of tasks A. We can then create an optimal schedule having the tasks in A as its early tasks. This method is an efficient algorithm for scheduling unit-time tasks with deadlines and penalties for a single processor. The running time is O(n2) using GREEDY, since each of the O(n) independence checks made by that algorithm takes time O(n) (see Exercise 17.5-2). A faster implementation is given in Problem 17-3.
Figure 17.7 gives an example of a problem of scheduling unit-time tasks with deadlines and penalties for a single processor. In this example, the greedy algorithm selects tasks 1, 2, 3, and 4, then rejects tasks 5 and 6, and finally accepts task 7. The final optimal schedule is
which has a total penalty incurred of w5 +w6 = 50.
17.5-1
Solve the instance of the scheduling problem given in Figure 17.7, but with each penalty wi replaced by 80 - wi.
17.5-2
Show how to use property 2 of Lemma 17.11 to determine in time O(|A|) whether or not a given set A of tasks is independent.
17-1 Coin changing
Consider the problem of making change for n cents using the least number of coins.
a. Describe a greedy algorithm to make change consisting of quarters, dimes, nickels, and pennies. Prove that your algorithm yields an optimal solution.
b. Suppose that the available coins are in the denominations c0, c1, . . . , ck for some integers c >1 and k
c. Give a set of coin denominations for which the greedy algorithm does not yield an optimal solution.
17-2 Acyclic subgraphs
a. Let G = (V, E) be an undirected graph. Using the definition of a matroid, show that
b. The incidence matrix for an undirected graph G = (V, E) is a |V| X |E| matrix M such that Mve = 1 if edge e is incident on vertex v, and Mve = 0 otherwise. Argue that a set of columns of M is linearly independent if and only if the corresponding set of edges is acyclic. Then, use the result of Exercise 17.4-2 to provide an alternate proof that
c. Suppose that a nonnegative weight w(e) is associated with each edge in an undirected graph G = ( V, E). Give an efficient algorithm to find an an acyclic subset of E of maximum total weight.
d. Let G(V, E) be an arbitrary directed graph, and let
e. The incidence matrix for a directed graph G= (V, E) is a |V| X |E| matrix M such that Mve = -1 if edge e leaves vertex v, Mve = 1 if edge e enters vertex v, and and Mve = 0 otherwise. Argue that if a set of edges of G is linearly independent, then the corresponding set of edges does not contain a directed cycle.
f. Exercise 17.4-2 tells us that the set of linearly independent sets of columns of any matrix M forms a matroid. Explain carefully why the results of parts (d) and (e) are not contradictory. How can there fail to be a perfect correspondence between the notion of a set of edges being acyclic and the notion of the associated set of columns of the incidence matrix being linearly independent?
17-3 Scheduling variations
Consider the following algorithm for solving the problem in Section 17.5 of scheduling unit-time tasks with deadlines and penalties. Let all n time slots be initially empty, where time slot i is the unit-length slot of time that finishes at time i. We consider the jobs in order of monotonically decreasing penalty. When considering job j, if there exists a time slot at or before j's deadline dj that is still empty, assign job j to the latest such slot, filling it. If there is no such slot, assign job j to the latest of the as yet unfilled slots.
a. Argue that this algorithm always gives an optional answer.
b. Use the fast disjoint-set forest presented in Section 22.3 to implement the algorithm efficiently. Assume that the set of input jobs has already been sorted into monotonically decreasing order by penalty. Analyze the running time of your implementation.
Much more material on greedy algorithms and matroids can be found in Lawler [132] and Papadimitriou and Steiglitz [154].
The greedy algorithm first appeared in the combinatorial optimization literature in a 1971 article by Edmonds [62], though the theory of matroids dates back to a 1935 article by Whitney [200].
Our proof of the correctness of the greedy algorithm for the activity-selection problem follows that of Gavril [80]. The task-scheduling problem is studied in Lawler [132], Horowitz and Sahni [105], and Brassard and Bratley [33].
Huffman codes were invented in 1952 [107]; Lelewer and Hirschberg [136] surveys data-compression techniques known as of 1987.
An extension of matroid theory to greedoid theory was pioneered by Korte and Lovász [127, 128, 129, 130], who greatly generalize the theory presented here.
 âi. If selected, activity i takes place during the half-open time interval [si,âi). Activities i and j are compatible if the intervals [si, âi) and [sj,âj) do not overlap (i.e., i and j are compatible if si
âi. If selected, activity i takes place during the half-open time interval [si,âi). Activities i and j are compatible if the intervals [si, âi) and [sj,âj) do not overlap (i.e., i and j are compatible if si  âj or sj
âj or sj  âi). The activity-selection problem is to select a maximum-size set of mutually compatible activities.
âi). The activity-selection problem is to select a maximum-size set of mutually compatible activities.â1
 â2
â2  . . .
. . .  ân .
ân .(17.1)
GREEDY-ACTIVITY-SELECTOR(s, f)
1 n
 length[s]
length[s]2 A
 {1}
{1}3 j
 1
14 for i
 2 to n
2 to n5 do if si
 âj
âj6 then A
 A
A  {i}
{i}7 j
 i
i8 return A
âj = max{fk : K  A}.
A}.(17.2)
 (n) time, assuming that the activities were already sorted initially by their finish times.
(n) time, assuming that the activities were already sorted initially by their finish times.
Figure 17.1 The operation of GREEDY-ACTIVITY-SELECTOR on 11 activities given at the left. Each row of the figure corresponds to an iteration of the for loop in lines 4-7. The activities that have been selected to be in set A are shaded, and activity i, shown in white, is being considered. If the starting time si of activity i occurs before the finishing time fj of the most recently selected activity j (the arrow between them points left), it is rejected. Otherwise (the arrow points directly up or to the right), it is accepted and put into set A.
Proving the greedy algorithm correct
 S is an optimal solution to the given instance of the activity-selection problem, and let us order the activities in A by finish time. Suppose further that the first activity in A is activity k. If k = 1, then schedule A begins with a greedy choice. If k
S is an optimal solution to the given instance of the activity-selection problem, and let us order the activities in A by finish time. Suppose further that the first activity in A is activity k. If k = 1, then schedule A begins with a greedy choice. If k  1, we want to show that there is another optimal solution B to S that begins with the greedy choice, activity 1. Let B = A - {k}
1, we want to show that there is another optimal solution B to S that begins with the greedy choice, activity 1. Let B = A - {k}  {1}. Because fi
{1}. Because fi  fk, the activities in B are disjoint, and since B has the same number of activities as A, it is also optimal. Thus, B is an optimal solution for S that contains the greedy choice of activity 1. Therefore, we have shown that there always exists an optimal schedule that begins with a greedy choice.
fk, the activities in B are disjoint, and since B has the same number of activities as A, it is also optimal. Thus, B is an optimal solution for S that contains the greedy choice of activity 1. Therefore, we have shown that there always exists an optimal schedule that begins with a greedy choice. S: Si
S: Si  f1}. Why? If we could find a solution B' to S' with more activities than A', adding activity 1 to B' would yield a solution B to S with more activities than A, thereby contradicting the optimality of A. Therefore, after each greedy choice is made, we are left with an optimization problem of the same form as the original problem. By induction on the number of choices made, making the greedy choice at every step produces an optimal solution.
f1}. Why? If we could find a solution B' to S' with more activities than A', adding activity 1 to B' would yield a solution B to S with more activities than A, thereby contradicting the optimality of A. Therefore, after each greedy choice is made, we are left with an optimization problem of the same form as the original problem. By induction on the number of choices made, making the greedy choice at every step produces an optimal solution. Exercises
17.2 Elements of the greedy strategy
Greedy-choice property
Optimal substructure
 S : si
S : si  â1}.
â1}.Greedy versus dynamic programming
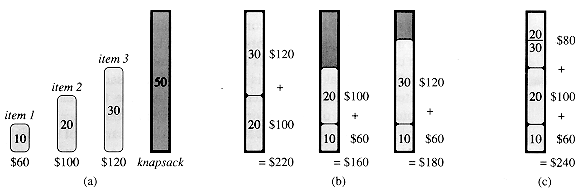
Figure 17.2 The greedy strategy does not work for the 0-1 knapsack problem. (a) The thief must select a subset of the three items shown whose weight must not exceed 50 pounds. (b) The optimal subset includes items 2 and 3. Any solution with item 1 is suboptimal, even though item 1 has the greatest value per pound. (c) For the fractional knapsack problem, taking the items in order of greatest value per pound yields an optimal solution.
Exercises
17.3 Huffman codes
a b c d e f
--------------------------------------------------------------
Frequency (in thousands) 45 13 12 16 9 5
Fixed-length codeword 000 001 010 011 100 101
Variable-length codeword 0 101 100 111 1101 1100
Figure 17.3 A character-coding problem. A data file of 100,000 characters contains only the characters a-f, with the frequencies indicated. If each character is assigned a 3-bit codeword, the file can be encoded in 300,000 bits. Using the variable-length code shown, the file can be encoded in 224,000 bits.
 1 + 13
1 + 13  3 + 12
3 + 12  3 + 16
3 + 16  3 + 9
3 + 9  4 + 5
4 + 5  4)
4)  1,000 = 224,000 bits to represent the file, a savings of approximately 25%. In fact, this is an optimal character code for this file, as we shall see.
1,000 = 224,000 bits to represent the file, a savings of approximately 25%. In fact, this is an optimal character code for this file, as we shall see.Prefix codes
 101
101  100 = 0101100, where we use "
100 = 0101100, where we use " " to denote concatenation.
" to denote concatenation. 0
0  101
101  1101, which decodes to aabe.
1101, which decodes to aabe.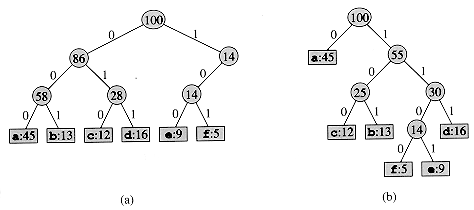
Figure 17.4 Trees corresponding to the coding schemes in Figure 17.3. Each leaf is labeled with a character and its frequency of occurrence. Each internal node is labeled with the sum of the weights of the leaves in its subtree. (a) The tree corresponding to the fixed-length code a = 000, . . . , f = 100. (b) The tree corresponding to the optimal prefix code a = 0, b = 101, . . . , f = 1100

(17.3)
Constructing a Huffman code
 C is an object with a defined frequency f[c]. A priority queue Q, keyed on f, is used to identify the two least-frequent objects to merge together. The result of the merger of two objects is a new object whose frequency is the sum of the frequencies of the two objects that were merged.
C is an object with a defined frequency f[c]. A priority queue Q, keyed on f, is used to identify the two least-frequent objects to merge together. The result of the merger of two objects is a new object whose frequency is the sum of the frequencies of the two objects that were merged.HUFFMAN(C)
1 n
 |C|
|C|2 Q
 C
C3 for i
 1 to n - 1
1 to n - 14 do z
 ALLOCATE-NODE()
ALLOCATE-NODE()5 x
 left[z]
left[z]  EXTRACT-MIN(Q)
EXTRACT-MIN(Q)6 y
 right[z]
right[z]  EXTRACT-MIN(Q)
EXTRACT-MIN(Q)7 f[z]
 f[x] + f[y]
f[x] + f[y]8 INSERT(Q, z)
9 return EXTRACT-MIN(Q)
Correctness of Huffman's algorithm
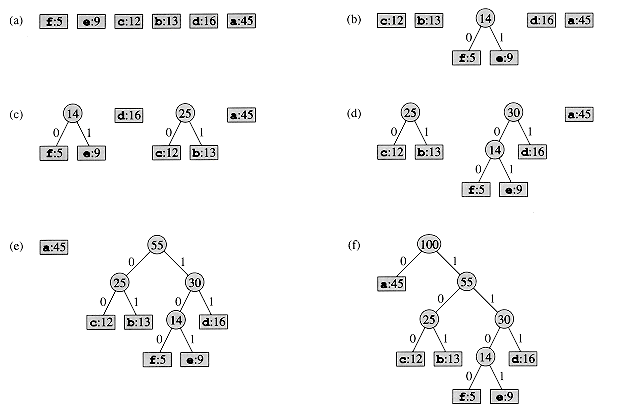
Figure 17.5 The steps of Huffman's algorithm for the frequencies given in Figure 17.3. Each part shows the contents of the queue sorted into increasing order by frequency. At each step, the two trees with lowest frequencies are merged. Leaves are shown as rectangles containing a character and its frequency. Internal nodes are shown as circles containing the sum of the frequencies of its children. An edge connecting an internal node with its children is labeled 0 if it is an edge to a left child and 1 if it is an edge to a right child. The codeword for a letter is the sequence of labels on the edges connecting the root to the leaf for that letter. (a) The initial set of n = 6 nodes, one for each letter. (b)-(e) Intermediate stages.(f) The final tree.

Figure 17.6 An illustration of the key step in the proof of Lemma 17.2. In the optimal tree T, leaves b and c are two of the deepest leaves and are siblings. Leaves x and y are the two leaves that Huffman's algorithm merges together first; they appear in arbitrary positions in T. Leaves b and x are swapped to obtain tree T'. Then, leaves c and y are swapped to obtain tree T\". Since each swap does not increase the cost, the resulting tree T\" is also an optimal tree.
 C has frequency f[c]. Let x and y be two characters in C having the lowest frequencies. Then there exists an optimal prefix code for C in which the codewords for x and y have the same length and differ only in the last bit.
C has frequency f[c]. Let x and y be two characters in C having the lowest frequencies. Then there exists an optimal prefix code for C in which the codewords for x and y have the same length and differ only in the last bit. f[c] and f[x]
f[c] and f[x]  f[y]. Since f[x] and f[y] are the two lowest leaf frequencies, in order, and f[b] and f[c] are two arbitrary frequencies, in order, we have f[x]
f[y]. Since f[x] and f[y] are the two lowest leaf frequencies, in order, and f[b] and f[c] are two arbitrary frequencies, in order, we have f[x]  f[b] and f[y]
f[b] and f[y]  f[c]. As shown in Figure 17.6, we exchange the positions in T of b and x to produce a tree T', and then we exchange the positions in T' of c and y to produce a tree T\". By equation (17.3), the difference in cost between T and T' is
f[c]. As shown in Figure 17.6, we exchange the positions in T of b and x to produce a tree T', and then we exchange the positions in T' of c and y to produce a tree T\". By equation (17.3), the difference in cost between T and T' is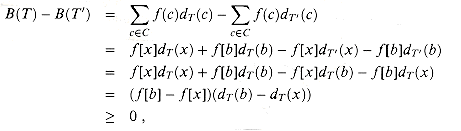
 B(T), and since T is optimal, B(T)
B(T), and since T is optimal, B(T)  B(T\"), which implies B(T\") = B(T). Thus, T\" is an optimal tree in which x and y appear as sibling leaves of maximum depth, from which the lemma follows.
B(T\"), which implies B(T\") = B(T). Thus, T\" is an optimal tree in which x and y appear as sibling leaves of maximum depth, from which the lemma follows.  C. Consider any two characters x and y that appear as sibling leaves in T, and let z be their parent. Then, considering z as a character with frequency f[z] = f[x] + f[y], the tree T' = T - {x,y} represents an optimal prefix code for the alphabet C' = C - {x,y}
C. Consider any two characters x and y that appear as sibling leaves in T, and let z be their parent. Then, considering z as a character with frequency f[z] = f[x] + f[y], the tree T' = T - {x,y} represents an optimal prefix code for the alphabet C' = C - {x,y}  {z}.
{z}. C - {x,y}, we have dT(c) = dT'(c), and hence f[c]dT(c) = f[c]dT'(c). Since dT(x) = dT(y) = dT'(z) + 1, we have
C - {x,y}, we have dT(c) = dT'(c), and hence f[c]dT(c) = f[c]dT'(c). Since dT(x) = dT(y) = dT'(z) + 1, we havef[x]dT(x) + f[y]dT(y) = (f[x]) + (f[y])dT'(z) + 1)
= f[z]dT'(z) + (f[x] + f[y]),
B(T) = B(T') + f[x] + f[y].
Exercises
a:1 b:1 c:2 d:3 e:5 f:8 g:13 h:21
2n - 1 + n
 lg n
lg n
* 17.4 Theoretical foundations for greedy methods
17.4.1 Matroids
 satisfying the following conditions.
satisfying the following conditions. is a nonempty family of subsets of S, called the independent subsets of S, such that if
is a nonempty family of subsets of S, called the independent subsets of S, such that if  and A
and A  B, then
B, then  . We say that
. We say that  is hereditary if it satisfies this property. Note that the empty set
is hereditary if it satisfies this property. Note that the empty set  is necessarily a member of
is necessarily a member of  .
. , and |A| < |B|, then there is some element x
, and |A| < |B|, then there is some element x  B - A such that
B - A such that  . We say that M satisfies the exchange property.
. We say that M satisfies the exchange property. defined in terms of a given undirected graph G = ( V, E) as follows.
defined in terms of a given undirected graph G = ( V, E) as follows. The set SG is defined to be E, the set of edges of G.
The set SG is defined to be E, the set of edges of G. If A is a subset of E, then
If A is a subset of E, then  if and only if A is acyclic. That is, a set of edges is independent if and only if it forms a forest.
if and only if A is acyclic. That is, a set of edges is independent if and only if it forms a forest. is a matroid.
is a matroid. is hereditary, since a subset of a forest is a forest. Putting it another way, removing edges from an acyclic set of edges cannot create cycles.
is hereditary, since a subset of a forest is a forest. Putting it another way, removing edges from an acyclic set of edges cannot create cycles. , we call an element x
, we call an element x  A an extension of
A an extension of  if x can be added to A while preserving independence; that is, x is an extension of A if
if x can be added to A while preserving independence; that is, x is an extension of A if  . As an example, consider a graphic matroid MG. If A is an independent set of edges, then edge e is an extension of A if and only if e is not in A and the addition of x to A does not create a cycle.
. As an example, consider a graphic matroid MG. If A is an independent set of edges, then edge e is an extension of A if and only if e is not in A and the addition of x to A does not create a cycle. {x} for some x
{x} for some x  B - A, contradicting the assumption that A is maximal.
B - A, contradicting the assumption that A is maximal.  is weighted if there is an associated weight function w that assigns a strictly positive weight w(x) to each element x
is weighted if there is an associated weight function w that assigns a strictly positive weight w(x) to each element x  S. The weight function w extends to subsets of S by summation:
S. The weight function w extends to subsets of S by summation: 
 S. For example, if we let w(e) denote the length of an edge e in a graphic matroid MG, then w(A) is the total length of the edges in edge set A.
S. For example, if we let w(e) denote the length of an edge e in a graphic matroid MG, then w(A) is the total length of the edges in edge set A.17.4.2 Greedy algorithms on a weighted matroid
 , and we wish to find an independent set
, and we wish to find an independent set  such that w(A) is maximized. We call such a subset that is independent and has maximum possible weight an optimal subset of the matroid. Because the weight w(x) of any element x
such that w(A) is maximized. We call such a subset that is independent and has maximum possible weight an optimal subset of the matroid. Because the weight w(x) of any element x  S is positive, an optimal subset is always a maximal independent subset--it always helps to make A as large as possible.
S is positive, an optimal subset is always a maximal independent subset--it always helps to make A as large as possible.w'(A) = (|V| - 1)w0 - w(A)
 with an an associated positive weight function w, and it returns an optimal subset A. In our pseudocode, we denote the components of M by S[M] and
with an an associated positive weight function w, and it returns an optimal subset A. In our pseudocode, we denote the components of M by S[M] and  and the weight function by w. The algorithm is greedy because it considers each element x
and the weight function by w. The algorithm is greedy because it considers each element x  S in turn in order of nonincreasing weight and immediately adds it to the set A being accumulated if A
S in turn in order of nonincreasing weight and immediately adds it to the set A being accumulated if A  {x} is independent.
{x} is independent.
 {x} is independent, the subset A is always independent, by induction. Therefore, GREEDY always returns an independent subset A. We shall see in a moment that A is a subset of maximum possible weight, so that A is an optimal subset.
{x} is independent, the subset A is always independent, by induction. Therefore, GREEDY always returns an independent subset A. We shall see in a moment that A is a subset of maximum possible weight, so that A is an optimal subset. {x} is independent. If each such check takes time O(f(n)), the entire algorithm runs in time O(n lg n + nf(n)).
{x} is independent. If each such check takes time O(f(n)), the entire algorithm runs in time O(n lg n + nf(n)). is a weighted matroid with weight function w and that S is sorted into nonincreasing order by weight. Let x be the first element of S such that {x} is independent, if any such x exists. If x exists, then there exists an optimal subset A of S that contains x.
is a weighted matroid with weight function w and that S is sorted into nonincreasing order by weight. Let x be the first element of S such that {x} is independent, if any such x exists. If x exists, then there exists an optimal subset A of S that contains x. B; otherwise, we let A = B and we're done.
B; otherwise, we let A = B and we're done. B implies that {y} is independent, since
B implies that {y} is independent, since  and I is hereditary. Our choice of x therefore ensures that w(x)
and I is hereditary. Our choice of x therefore ensures that w(x)  w(y) for any y
w(y) for any y  B.
B. {x} for some y
{x} for some y  B, and so
B, and sow(A) = w(B) - w(y) + w(x)
 w(B) .
w(B) . A, the lemma is proven.
A, the lemma is proven.  be any matroid. If x is an element of S such that x is not an extension of
be any matroid. If x is an element of S such that x is not an extension of  , then x is not an extension of any independent subset A of S.
, then x is not an extension of any independent subset A of S. . Since x is an extension of A, we have that A
. Since x is an extension of A, we have that A  {x} is independent. Since
{x} is independent. Since  is hereditary, {x} must be independent, which contradicts the assumption that x is not an extension of
is hereditary, {x} must be independent, which contradicts the assumption that x is not an extension of  .
.  , since they can never be used.
, since they can never be used. . The remaining problem of finding a maximum-weight independent subset containing x reduces to finding a maximum-weight independent subset of the weighted matroid
. The remaining problem of finding a maximum-weight independent subset containing x reduces to finding a maximum-weight independent subset of the weighted matroid  , where
, where
 {x} of M. Since we have in both cases that w(A) = w(A') + w(x), a maximum-weight solution in M containing x yields a maximum-weight solution in M', and vice versa.
{x} of M. Since we have in both cases that w(A) = w(A') + w(x), a maximum-weight solution in M containing x yields a maximum-weight solution in M', and vice versa. is a weighted matroid with weight function w, then the call GREEDY(M, w) returns an optimal subset.
is a weighted matroid with weight function w, then the call GREEDY(M, w) returns an optimal subset. can be forgotten about, since they can never be useful. Once the first element x is selected, Lemma 17.7 implies that GREEDY does not err by adding x to A, since there exists an optimal subset containing x. Finally, Lemma 17.9 implies that the remaining problem is one of finding an optimal subset in the matroid M' that is the contraction of M by x. After the procedure GREEDY sets A to{x}, all of its remaining steps can be interpreted as acting in the matroid
can be forgotten about, since they can never be useful. Once the first element x is selected, Lemma 17.7 implies that GREEDY does not err by adding x to A, since there exists an optimal subset containing x. Finally, Lemma 17.9 implies that the remaining problem is one of finding an optimal subset in the matroid M' that is the contraction of M by x. After the procedure GREEDY sets A to{x}, all of its remaining steps can be interpreted as acting in the matroid  , because B is independent in M' if and only if B
, because B is independent in M' if and only if B  {x} is independent in M, for all sets
{x} is independent in M, for all sets  . Thus, the subsequent operation of GREEDY will find a maximum-weight independent subset for M', and the overall operation of GREEDY will find a maximum-weight independent subset for M.
. Thus, the subsequent operation of GREEDY will find a maximum-weight independent subset for M', and the overall operation of GREEDY will find a maximum-weight independent subset for M. Exercises
 is a matroid, where S is any finite set and
is a matroid, where S is any finite set and  is the set of all subsets of S of size at most k, where k
is the set of all subsets of S of size at most k, where k  |S|.
|S|. n real-valued matrix T, show that
n real-valued matrix T, show that  is a matroid, where S is the set of columns of T and
is a matroid, where S is the set of columns of T and  if and only if the columns in A are linearly independent.
if and only if the columns in A are linearly independent. is a matroid, then
is a matroid, then  is a matroid, where
is a matroid, where  contains some maximal
contains some maximal  . That is, the maximal independent sets of
. That is, the maximal independent sets of  are just the complements of the maximal independent sets of
are just the complements of the maximal independent sets of  .
. by the condition that
by the condition that  . Show that
. Show that  is a matroid. That is, the set of all sets A that contain at most one member in each block of the partition determines the independent sets of a matroid.
is a matroid. That is, the set of all sets A that contain at most one member in each block of the partition determines the independent sets of a matroid.* 17.5 A task-scheduling problem
 a set S = {1, 2, . . . , n} of n unit-time tasks;
a set S = {1, 2, . . . , n} of n unit-time tasks; a set of n integer deadlines d1, d2, . . . , dn, such that each di satisfies 1
a set of n integer deadlines d1, d2, . . . , dn, such that each di satisfies 1  di
di  n and task i is supposed to finish by time di; and
n and task i is supposed to finish by time di; and a set of n nonnegative weights or penalties w1,w2, . . . , wn, such that a penalty wi is incurred if task i is not finished by time di and no penalty is incurred if a task finishes by its deadline.
a set of n nonnegative weights or penalties w1,w2, . . . , wn, such that a penalty wi is incurred if task i is not finished by time di and no penalty is incurred if a task finishes by its deadline. dj. Therefore, k + 1 < di, and so task i is still early after the swap. Task j is moved earlier in the schedule, so it also still early after the swap.
dj. Therefore, k + 1 < di, and so task i is still early after the swap. Task j is moved earlier in the schedule, so it also still early after the swap. denote the set of all independent sets of tasks.
denote the set of all independent sets of tasks. t.
t. is the set of all independent sets of tasks, then the corresponding system
is the set of all independent sets of tasks, then the corresponding system  is a matroid.
is a matroid. Nt(A). Since Nn(B) = |B| and Nn(A) = |A|, but |B| > |A|, we must have that k < n and that Nj(B) > Nj(A) for all j in the range k + 1
Nt(A). Since Nn(B) = |B| and Nn(A) = |A|, but |B| > |A|, we must have that k < n and that Nj(B) > Nj(A) for all j in the range k + 1  j
j  n. Therefore, B contains more tasks with deadline k + 1 than A does. Let x be a task in B - A with deadline k + 1. Let A' = A = A
n. Therefore, B contains more tasks with deadline k + 1 than A does. Let x be a task in B - A with deadline k + 1. Let A' = A = A  {x}.
{x}. t
t  k, we have Nt(A') = Nt(A)
k, we have Nt(A') = Nt(A)  t,since A is independent. For k < t
t,since A is independent. For k < t  n, we have Nt(A')
n, we have Nt(A')  Nt(B)
Nt(B)  t, since B is independent. Therefore, A' is independent, completing our proof that
t, since B is independent. Therefore, A' is independent, completing our proof that  is a matroid.
is a matroid. Task
1 2 3 4 5 6 7
-------------------------------
di 4 2 4 3 1 4 6
wi 70 60 50 40 30 20 10
Figure 17.7 An instance of the problem of scheduling unit-time tasks with deadlines and penalties for a single processor.
 2, 4, 1, 3, 7, 5, 6
2, 4, 1, 3, 7, 5, 6 ,
,Exercises
Problems
 1. Show that the greedy algorithm always yields an optimal solution.
1. Show that the greedy algorithm always yields an optimal solution. ) is a matroid, where
) is a matroid, where  if and only if A is an acyclic subset of E.
if and only if A is an acyclic subset of E. of part (a) is matroid.
of part (a) is matroid. ) be defined so that
) be defined so that  if and only if A does not contain any directed cycles. Give an example of a directed graph G such that the associated system
if and only if A does not contain any directed cycles. Give an example of a directed graph G such that the associated system  ) is not a matroid. Specify which defining condition for a matroid fails to hold.
) is not a matroid. Specify which defining condition for a matroid fails to hold.Chapter notes


