The adjacency-list representation of a graph G = (V, E) consists of an array Adj of |V| lists, one for each vertex in V. For each u
If G is a directed graph, the sum of the lengths of all the adjacency lists is |E|, since an edge of the form (u,v) is represented by having v appear in Adj[u]. If G is an undirected graph, the sum of the lengths of all the adjacency lists is 2|E|, since if (u,v) is an undirected edge, then u appears in v's adjacency list and vice versa. Whether a graph is directed or not, the adjacency-list representation has the desirable property that the amount of memory it requires is O(max(V, E)) = O(V + E).
Adjacency lists can readily be adapted to represent weighted graphs, that is, graphs for which each edge has an associated weight, typically given by a weight function w : E
A potential disadvantage of the adjacency-list representation is that there is no quicker way to determine if a given edge (u,v) is present in the graph than to search for v in the adjacency list Adj[u]. This disadvantage can be remedied by an adjacency-matrix re presentation of the graph, at the cost of using asymptotically more memory.
For the adjacency-matrix representation of a graph G = (V, E), we assume that the vertices are numbered 1, 2, . . . , |V| in some arbitrary manner. The adjacency-matrix representation of a graph G then consists of a |V|
Figures 23.1(c) and 23.2(c) are the adjacency matrices of the undirected and directed graphs in Figures 23.1(a) and 23.2(a), respectively. The adjacency matrix of a graph requires
Observe the symmetry along the main diagonal of the adjacency matrix in Figure 23.1(c). We define the the transpose of a matrix A = (aij) to be the matrix
Like the adjacency-list representation of a graph, the adjacency-matrix representation can be used for weighted graphs. For example, if G = (V, E) is a weighted graph with edge-weight function w, the weight w(u, v) of the edge (u,v)
Although the adjacency-list representation is asymptotically at least as efficient as the adjacency-matrix representation, the simplicity of an adjacency matrix may make it preferable when graphs are reasonably small. Moreover, if the graph is unweighted, there is an additional advantage in storage for the adjacency-matrix representation. Rather than using one word of computer memory for each matrix entry, the adjacency matrix uses only one bit per entry.
23.1-1
Given an adjacency-list representation of a directed graph, how long does it take to compute the out-degree of every vertex? How long does it take to compute the in-degrees?
23.1-2
Give an adjacency-list representation for a complete binary tree on 7 vertices. Give an equivalent adjacency-matrix representation. Assume that vertices are numbered from 1 to 7 as in a binary heap.
23.1-3
The transpose of a directed graph G = (V, E) is the graph GT = (V, ET), where ET = {(v,u)
23.1-4
Given an adjacency-list representation of a multigraph G = (V, E), describe an O(V+E)-time algorithm to compute the adjacency-list representation of the "equivalent" undirected graph G' = (V, E'), where E' consists of the edges in E with all multiple edges between two vertices replaced by a single edge and with all self-loops removed.
23.1-5
The square of a directed graph G = (V, E) is the graph G2 = (V, E2) such that (u,w)
23.1-6
When an adjacency-matrix representation is used, most graph algorithms require time
23.1-7
The incidence matrix of a directed graph G = (V, E) is a |V|
Describe what the entries of the matrix product BBT represent, where BT is the transpose of B.
Breadth-first search is one of the simplest algorithms for searching a graph and the archetype for many important graph algorithms. Dijkstra's single-source shortest-paths algorithm (Chapter 25) and Prim's minimum-spanning-tree algorithm (Section 24.2) use ideas similar to those in breadth-first search.
Given a graph G = (V, E) and a distinguished source vertex s, breadth-first search systematically explores the edges of G to "discover" every vertex that is reachable from s. It computes the distance (fewest number of edges) from s to all such reachable vertices. It also produces a "breadth-first tree" with root s that contains all such reachable vertices. For any vertex v reachable from s, the path in the breadth-first tree from s to v corresponds to a "shortest path" from s to v in G, that is, a path containing the fewest number of edges. The algorithm works on both directed and undirected graphs.
Breadth-first search is so named because it expands the frontier between discovered and undiscovered vertices uniformly across the breadth of the frontier. That is, the algorithm discovers all vertices at distance k from s before discovering any vertices at distance k + 1.
To keep track of progress, breadth-first search colors each vertex white, gray, or black. All vertices start out white and may later become gray and then black. A vertex is discovered the first time it is encountered during the search, at which time it becomes nonwhite. Gray and black vertices, therefore, have been discovered, but breadth-first search distinguishes between them to ensure that the search proceeds in a breadth-first manner. If (u, v)
Breadth-first search constructs a breadth-first tree, initially containing only its root, which is the source vertex s. Whenever a white vertex v is discovered in the course of scanning the adjacency list of an already discovered vertex u, the vertex v and the edge (u,v) are added to the tree. We say that u is the predecessor or parent of v in the breadth-first tree. Since a vertex is discovered at most once, it has at most one parent. Ancestor and descendant relationships in the breadth-first tree are defined relative to the root s as usual: if u is on a path in the tree from the root s to vertex v, then u is an ancestor of v and v is a descendant of u.
The breadth-first-search procedure BFS below assumes that the input graph G = (V, E) is represented using adjacency lists. It maintains several additional data structures with each vertex in the graph. The color of each vertex u
Figure 23.3 illustrates the progress of BFS on a sample graph.
The procedure BFS works as follows. Lines 1-4 paint every vertex white, set d [u] to be infinity for every vertex u, and set the parent of every vertex to be NIL. Line 5 paints the source vertex s gray, since it is considered to be discovered when the procedure begins. Line 6 initializes d[s] to 0, and line 7 sets the predecessor of the source to be NIL. Line 8 initializes Q to the queue containing just the vertex s; thereafter, Q always contains the set of gray vertices.
The main loop of the program is contained in lines 9-18. The loop iterates as long as there remain gray vertices, which are discovered vertices that have not yet had their adjacency lists fully examined. Line 10 determines the gray vertex u at the head of the queue Q. The for loop of lines 11-16 considers each vertex v in the adjacency list of u. If v is white, then it has not yet been discovered, and the algorithm discovers it by executing lines 13-16. It is first grayed, and its distance d[v] is set to d[u] + 1. Then, u is recorded as its parent. Finally, it is placed at the tail of the queue Q. When all the vertices on u's adjacency list have been examined, u is removed from Q and blackened in lines 17-18.
Before proving all the various properties of breadth-first search, we take on the somewhat easier job of analyzing its running time on an input graph G = (V,E). After initialization, no vertex is ever whitened, and thus the test in line 12 ensures that each vertex is enqueued at most once, and hence dequeued at most once. The operations of enqueuing and dequeuing take O(1) time, so the total time devoted to queue operations is O(V). Because the adjacency list of each vertex is scanned only when the vertex is dequeued, the adjacency list of each vertex is scanned at most once. Since the sum of the lengths of all the adjacency lists is
At the beginning of this section, we claimed that breadth-first search finds the distance to each reachable vertex in a graph G = (V,E) from a given source vertex s
1 In Chapters 25 and 26, we shall generalize our study of shortest paths to weighted graphs, in which every edge has a real-valued weight and the weight of a path is the sum of the weights of its constituent edges. The graphs considered in the present chapter are unweighted.
Lemma 23.1
Let G = (V,E) be a directed or undirected graph, and let s
Proof If u is reachable from s, then so is v. In this case, the shortest path from s to v cannot be longer than the shortest path from s to v followed by the edge (u, v), and thus the inequality holds. If u is not reachable from s, then
We want to show that BFS properly computes d[v] =
Lemma 23.2
Let G = (V,E) be a directed or undirected graph, and suppose that BFS is run on G from a given source vertex s
Proof We use induction on the number of times a vertex is placed in the queue Q. Our inductive hypothesis is that d[v]
The basis of the induction is the situation immediately after s is placed in Q in line 8 of BFS. The inductive hypothesis holds here, because d[s] = 0 =
For the inductive step, consider a white vertex v that is discovered during the search from a vertex u. The inductive hypothesis implies that d[u]
Vertex v is then inserted into the queue Q, and it is never inserted again because it is also grayed and the then clause of lines 13-16 is executed only for white vertices. Thus, the value of d[v] never changes again, and the inductive hypothesis is maintained.
To prove that d[v] =
Lemma 23.3
Suppose that during the execution of BFS on a graph G = (V, E), the queue Q contains the vertices
Proof The proof is by induction on the number of queue operations. Initially, when the queue contains only s, the lemma certainly holds.
For the inductive step, we must prove the lemma holds after both dequeuing and enqueuing a vertex. If the head v1 of the queue is dequeued, the new head is v2. (If the queue becomes empty, then the lemma holds vacuously.) But then we have d[vr]
We can now prove that breadth-first search correctly finds shortest-path distances.
Theorem 23.4
Let G = (V, E) be a directed or undirected graph, and suppose that BFS is run on G from a given source vertex s
Proof We start with the case in which v is unreachable from s. Since Lemma 23.2 gives d[v]
The main part of the proof is for vertices reachable from s. Let Vk denote the set of vertices at distance k from s; that is, Vk = {v
As we have noted before, there is certainly at most one such point.
The basis is for k = 0. We have V0 = {s}, since the source s is the only vertex at distance 0 from s. During the initialization, s is grayed, d[s] is set to 0, and s is placed into Q, so the inductive hypothesis holds.
For the inductive step, we start by noting that the queue Q is never empty until the algorithm terminates and that, once a vertex u is inserted into the queue, neither d[u] nor
Now let us consider an arbitrary vertex v
Since
To conclude the proof of the lemma, observe that if v
The procedure BFS builds a breadth-first tree as it searches the graph, as illustrated in Figure 23.3. The tree is represented by the
and
The predecessor subgraph G
After BFS has been run from a source s on a graph G, the following lemma shows that the predecessor subgraph is a breadth-first tree.
Lemma 23.5
When applied to a directed or undirected graph G = (V, E), procedure BFS constructs
Proof Line 15 of BFS only sets
The following procedure prints out the vertices on a shortest path from s to v, assuming that BFS has already been run to compute the shortest-path tree.
This procedure runs in time linear in the number of vertices in the path printed, since each recursive call is for a path one vertex shorter.
23.2-1
Show the result of running breadth-first search on the directed graph of Figure 23.2(a), using vertex 3 as the source.
23.2-2
Show the result of running breadth-first search on the undirected graph of Figure 23.3, using vertex u as the source.
23.2-3
What is the running time of BFS if its input graph is represented by an adjacency matrix and the algorithm is modified to handle this form of input?
23.2-4
Argue that in a breadth-first search, the value d[u] assigned to a vertex u is independent of the order in which the vertices in each adjacency list are given.
23.2-5
Give an example of a directed graph G = (V, E), a source vertex s
23.2-6
Give an efficient algorithm to determine if an undirected graph is bipartite.
23.2-7
The diameter of a tree T = (V, E) is given by
that is, the diameter is the largest of all shortest-path distances in the tree. Give an efficient algorithm to compute the diameter of a tree, and analyze the running time of your algorithm.
23.2-8
Let G = (V, E) be an undirected graph. Give an O(V + E)-time algorithm to compute a path in G that traverses each edge in E exactly once in each direction. Describe how you can find your way out of a maze if you are given a large supply of pennies.
The strategy followed by depth-first search is, as its name implies, to search "deeper" in the graph whenever possible. In depth-first search, edges are explored out of the most recently discovered vertex v that still has unexplored edges leaving it. When all of v's edges have been explored, the search "backtracks" to explore edges leaving the vertex from which v was discovered. This process continues until we have discovered all the vertices that are reachable from the original source vertex. If any undiscovered vertices remain, then one of them is selected as a new source and the search is repeated from that source. This entire process is repeated until all vertices are discovered.
As in breadth-first search, whenever a vertex v is discovered during a scan of the adjacency list of an already discovered vertex u, depth-first search records this event by setting v's predecessor field
The predecessor subgraph of a depth-first search forms a depth-first forest composed of several depth-first trees. The edges in E
As in breadth-first search, vertices are colored during the search to indicate their state. Each vertex is initially white, is grayed when it is discovered in the search, and is blackened when it is finished, that is, when its adjacency list has been examined completely. This technique guarantees that each vertex ends up in exactly one depth-first tree, so that these trees are disjoint.
Besides creating a depth-first forest, depth-first search also timestamps each vertex. Each vertex v has two timestamps: the first timestamp d[v] records when v is first discovered (and grayed), and the second timestamp f[v] records when the search finishes examining v's adjacency list (and blackens v). These timestamps are used in many graph algorithms and are generally helpful in reasoning about the behavior of depth-first search.
The procedure DFS below records when it discovers vertex u in the variable d[u] and when it finishes vertex u in the variable f[u]. These timestamps are integers between 1 and 2 |V|, since there is one discovery event and one finishing event for each of the |V| vertices. For every vertex u,
Vertex u is WHITE before time d[u], GRAY between time d[u] and time f[u], and BLACK thereafter.
The following pseudocode is the basic depth-first-search algorithm. The input graph G may be undirected or directed. The variable time is a global variable that we use for timestamping.
Figure 23.4 illustrates the progress of DFS on the graph shown in Figure 23.2.
Procedure DFS works as follows. Lines 1-3 paint all vertices white and initialize their
In each call DFS-VISIT(u), vertex u is initially white. Line 1 paints u gray, and line 2 records the discovery time d[u] by incrementing and saving the global variable time. Lines 3-6 examine each vertex v adjacent to u and recursively visit v if it is white. As each vertex v
What is the running time of DFS? The loops on lines 1-2 and lines 5-7 of DFS take time
the total cost of executing lines 2-5 of DFS-VISIT is
Depth-first search yields much information about the structure of a graph. Perhaps the most basic property of depth-first search is that the predecessor subgraph G
Another important property of depth-first search is that discovery and finishing times have parenthesis structure. If we represent the discovery of vertex u with a left parenthesis "(u" and represent its finishing by a right parenthesis "u)," then the history of discoveries and finishings makes a well-formed expression in the sense that the parentheses are properly nested. For example, the depth-first search of Figure 23.5(a) corresponds to the parenthesization shown in Figure 23.5(b). Another way of stating the condition of parenthesis structure is given in the following theorem.
Theorem 23.6
In any depth-first search of a (directed or undirected) graph G = (V, E), for any two vertices u and v, exactly one of the following three conditions holds:
Proof We begin with the case in which d[u] < d[v]. There are two subcases to consider, according to whether d[v] < â[u] or not. In the first subcase, d[v] < â[u], so v was discovered while u was still gray. This implies that v is a descendant of u. Moreover, since v was discovered more recently than u, all of its outgoing edges are explored, and v is finished, before the search returns to and finishes u. In this case, therefore, the interval [d[v],â[v]] is entirely contained within the interval [d[u],â[u]]. In the other subcase, â[u] < d[v], and inequality (23.1) implies that the intervals [d[u],â[u]] and [d[v],â[v]] are disjoint.
The case in which d[v] < d[u] is similar, with the roles of u and v reversed in the above argument.
Corollary 23.7
Vertex v is a proper descendant of vertex u in the depth-first forest for a (directed or undirected) graph G if and only if d[u] < d[v] < â[v] < â[u].
Proof Immediate from Theorem 23.6.
The next theorem gives another important characterization of when one vertex is a descendant of another in the depth-first forest.
Theorem 23.8
In a depth-first forest of a (directed or undirected) graph G = (V, E), vertex v is a descendant of vertex u if and only if at the time d[u] that the search discovers u, vertex v can be reached from u along a path consisting entirely of white vertices.
Proof
Another interesting property of depth-first search is that the search can be used to classify the edges of the input graph G = (V, E). This edge classification can be used to glean important information about a graph. For example, in the next section, we shall see that a directed graph is acyclic if and only if a depth-first search yields no "back" edges (Lemma 23.10).
We can define four edge types in terms of the depth-first forest G
1. Tree edges are edges in the depth-first forest G
2. Back edges are those edges (u, v) connecting a vertex u to an ancestor v in a depth-first tree. Self-loops are considered to be back edges.
3. Forward edges are those nontree edges (u, v) connecting a vertex u to a descendant v in a depth-first tree.
4. Cross edges are all other edges. They can go between vertices in the same depth-first tree, as long as one vertex is not an ancestor of the other, or they can go between vertices in different depth-first trees.
In Figures 23.4 and 23.5, edges are labeled to indicate their type. Figure 23.5(c) also shows how the graph of Figure 23.5(a) can be redrawn so that all tree and forward edges head downward in a depth-first tree and all back edges go up. Any graph can be redrawn in this fashion.
The DFS algorithm can be modified to classify edges as it encounters them. The key idea is that each edge (u, v) can be classified by the color of the vertex v that is reached when the edge is first explored (except that forward and cross edges are not distinguished):
1. WHITE indicates a tree edge,
2. GRAY indicates a back edge, and
3. BLACK indicates a forward or cross edge.
The first case is immediate from the specification of the algorithm. For the second case, observe that the gray vertices always form a linear chain of descendants corresponding to the stack of active DFS-VISIT invocations; the number of gray vertices is one more than the depth in the depth-first forest of the vertex most recently discovered. Exploration always proceeds from the deepest gray vertex, so an edge that reaches another gray vertex reaches an ancestor. The third case handles the remaining possibility; it can be shown that such an edge (u, v) is a forward edge if d[u] < d[v] and a cross edge if d[u] > d[v]. (See Exercise 23.3-4.)
In an undirected graph, there may be some ambiguity in the type classification, since (u, v) and (v, u) are really the same edge. In such a case, the edge is classified as the first type in the classification list that applies. Equivalently (see Exercise 23.3-5), the edge is classified according to whichever of (u, v) or (v, u) is encountered first during the execution of the algorithm.
We now show that forward and cross edges never occur in a depth-first search of an undirected graph.
Theorem 23.9
In a depth-first search of an undirected graph G, every edge of G is either a tree edge or a back edge.
Proof Let (u, v) be an arbitrary edge of G, and suppose without loss of generality that d[u] < d[v]. Then, v must be discovered and finished before we finish u, since v is on u's adjacency list. If the edge (u, v) is explored first in the direction from u to v, then (u, v) becomes a tree edge. If (u, v) is explored first in the direction from v to u, then (u, v) is a back edge, since u is still gray at the time the edge is first explored.
We shall see many applications of these theorems in the following sections.
23.3-1
Make a 3-by-3 chart with row and column labels WHITE, GRAY, and BLACK. In each cell (i, j), indicate whether, at any point during a depth-first search of a directed graph, there can be an edge from a vertex of color i to a vertex of color j. For each possible edge, indicate what edge types it can be. Make a second such chart for depth-first search of an undirected graph.
23.3-2
Show how depth-first search works on the graph of Figure 23.6. Assume that the for loop of lines 5-7 of the DFS procedure considers the vertices in alphabetical order, and assume that each adjacency list is ordered alphabetically. Show the discovery and finishing times for each vertex, and show the classification of each edge.
23.3-3
Show the parenthesis structure of the depth-first search shown in Figure 23.4.
23.3-4
Show that edge (u,v) is
a. a tree edge or forward edge if and only if d[u] < d[v] < f[v] < f[u],
b. a back edge if and only if d[v] < d[u] < f[u] < f[v], and
c. a cross edge if and only if d[v] < f[v] < d[u] < f[u].
23.3-5
Show that in an undirected graph, classifying an edge (u, v) as a tree edge or a back edge according to whether (u,v) or (v,u) is encountered first during the depth-first search is equivalent to classifying it according to the priority of types in the classification scheme.
23.3-6
Give a counterexample to the conjecture that if there is a path from u to v in a directed graph G, and if d[u] < d[v] in a depth-first search of G, then v is a descendant of u in the depth-first forest produced.
23.3-7
Modify the pseudocode for depth-first search so that it prints out every edge in the directed graph G, together with its type. Show what modifications, if any, must be made if G is undirected.
23.3-8
Explain how a vertex u of a directed graph can end up in a depth-first tree containing only u, even though u has both incoming and outgoing edges in G.
23.3-9
Show that a depth-first search of an undirected graph G can be used to identify the connected components of G, and that the depth-first forest contains as many trees as G has connected components. More precisely, show how to modify depth-first search so that each vertex v is assigned an integer label cc[v] between 1 and k, where k is the number of connected components of G, such that cc[u] = cc[v] if and only if u and v are in the same connected component.
23.3-10
A directed graph G = (V, E) is singly connected if
This section shows how depth-first search can be used to perform topological sorts of directed acyclic graphs, or "dags" as they are sometimes called. A topological sort of a dag G = (V, E) is a linear ordering of all its vertices such that if G contains an edge (u, v), then u appears before v in the ordering. (If the graph is not acyclic, then no linear ordering is possible.) A topological sort of a graph can be viewed as an ordering of its vertices along a horizontal line so that all directed edges go from left to right. Topological sorting is thus different from the usual kind of "sorting" studied in Part II.
Directed acyclic graphs are used in many applications to indicate precedences among events. Figure 23.7 gives an example that arises when Professor Bumstead gets dressed in the morning. The professor must don certain garments before others (e.g., socks before shoes). Other items may be put on in any order (e.g., socks and pants). A directed edge (u,v) in the dag of Figure 23.7(a) indicates that garment u must be donned before garment v. A topological sort of this dag therefore gives an order for getting dressed. Figure 23.7(b) shows the topologically sorted dag as an ordering of vertices along a horizontal line such that all directed edges go from left to right.
The following simple algorithm topologically sorts a dag.
Figure 23.7(b) shows how the topologically sorted vertices appear in reverse order of their finishing times.
We can perform a topological sort in time
We prove the correctness of this algorithm using the following key lemma characterizing directed acyclic graphs.
Lemma 23.10
A directed graph G is acyclic if and only if a depth-first search of G yields no back edges.
Proof
Theorem 23.11
TOPOLOGICAL-SORT(G) produces a topological sort of a directed acyclic graph G.
Proof Suppose that DFS is run on a given dag G = (V, E) to determine finishing times for its vertices. It suffices to show that for any pair of distinct vertices u,v
23.4-1
Show the ordering of vertices produced by TOPOLOGICAL-SORT when it is run on the dag of Figure 23.8.
23.4-2
There are many different orderings of the vertices of a directed graph G that are topological sorts of G. TOPOLOGICAL-SORT produces the ordering that is the reverse of the depth-first finishing times. Show that not all topological sorts can be produced in this way: there exists a graph G such that one of the topological sorts of G cannot be produced by TOPOLOGICAL-SORT, no matter what adjacency-list structure is given for G. Show also that there exists a graph for which two distinct adjacency-list representations yield the same topological sort.
23.4-3
Give an algorithm that determines whether or not a given undirected graph G = (V, E) contains a cycle. Your algorithm should run in O(V) time, independent of |E|.
23.4-4
Prove or disprove: If a directed graph G contains cycles, then TOPOLOGICAL-SORT(G) produces a vertex ordering that minimizes the number of "bad" edges that are inconsistent with the ordering produced.
23.4-5
Another way to perform topological sorting on a directed acyclic graph G = (V, E) is to repeatedly find a vertex of in-degree 0, output it, and remove it and all of its outgoing edges from the graph. Explain how to implement this idea so that it runs in time O(V + E). What happens to this algorithm if G has cycles?
We now consider a classic application of depth-first search: decomposing a directed graph into its strongly connected components. This section shows how to do this decomposition using two depth-first searches. Many algorithms that work with directed graphs begin with such a decomposition; this approach often allows the original problem to be divided into subproblems, one for each strongly connected component. Combining the solutions to the subproblems follows the structure of connections between strongly connected components; this structure can be represented by a graph known as the "component" graph, defined in Exercise 23.5-4.
Recall from Chapter 5 that a strongly connected component of a directed graph G = (V, E) is a maximal set of vertices U
Our algorithm for finding strongly connected components of a graph G = (V, E) uses the transpose of G, which is defined in Exercise 23.1-3 to be the graph GT = (V, ET), where ET = {(u, v): (v, u)
The following linear-time (i.e.,
This simple-looking algorithm seems to have nothing to do with strongly connected components. In the remainder of this section, we unravel the mystery of its design and prove its correctness. We begin with two useful observations.
Lemma 23.12
If two vertices are in the same strongly connected component, then no path between them ever leaves the strongly connected component.
Proof Let u and v be two vertices in the same strongly connected component. By the definition of strongly connected component, there are paths from u to v and from v to u. Let vertex w be on some path
Theorem 23.13
In any depth-first search, all vertices in the same strongly connected component are placed in the same depth-first tree.
Proof Of the vertices in the strongly connected component, let r be the first discovered. Because r is first, the other vertices in the strongly connected component are white at the time it is discovered. There are paths from r to every other vertex in the strongly connected component; because these paths never leave the strongly connected component (by Lemma 23.12), all vertices on them are white. Thus, by the white-path theorem, every vertex in the strongly connected component becomes a descendant of r in the depth-first tree.
In the rest of this section, the notations d[u] and f[u] refer to the discovery and finishing times as computed by the first depth-first search in line 1 of STRONGLY-CONNECTED-COMPONENTS. Similarly, the notation
To prove STRONGLY-CONNECTED-COMPONENTS correct, we introduce the notion of the forefather
Note that
We can also show that
since
As we shall see, every strongly connected component has one vertex that is the forefather of every vertex in the strongly connected component; this forefather is a "representative vertex" for the strongly connected component. In the depth-first search of G, it is the first vertex of the strongly connected component to be discovered, and it is the last vertex of the strongly connected component to be finished. In the depth-first search of GT, it is the root of a depth-first tree. We now prove these properties.
The first theorem justifies calling ø(u) a "forefather" of u.
Theorem 23.14
In a directed graph G = (V, E), the forefather
Proof If
It thus remains to prove that
1. If every intermediate vertex is white, then
2. If some intermediate vertex is nonwhite, let t be the last nonwhite vertex on the path from u to
Corollary 23.15
In any depth-first search of a directed graph G = (V, E), vertices u and ø(u), for all u
Proof We have
The following theorem gives a stronger result relating forefathers to strongly connected components.
Theorem 23.16
In a directed graph G = (V, E), two vertices u, v
Proof
With Theorem 23.16 in hand, the structure of the algorithm STRONGLY-CONNECTED-COMPONENTS can be more readily understood. The strongly connected components are sets of vertices with the same forefather. Moreover, by Theorem 23.14 and the parenthesis theorem (Theorem 23.6), during the depth-first search in line l of STRONGLY-CONNECTED-COMPONENTS a forefather is both the first vertex discovered and the last vertex finished in its strongly connected component.
To understand why we run the depth-first search in line 3 of STRONGLY-CONNECTED-COMPONENTS on GT, consider the vertex r with the largest finishing time computed by the depth-first search in line 1. By the definition of forefather, vertex r must be a forefather, since it is its own forefather: it can reach itself, and no vertex in the graph has a higher finishing time. What are the other vertices in r's strongly connected component? They are those vertices that have r as a forefather--those that can reach r but cannot reach any vertex with a finishing time greater than f[r]. But r's finishing time is the maximum of any vertex in G; thus, r's strongly connected component consists simply of those vertices that can reach r. Equivalently, r's strongly connected component consists of those vertices that r can reach in GT. Thus, the depth-first search in line 3 identifies all the vertices in r's strongly connected component and blackens them. (A breadth-first search, or any search for reachable vertices, could identify this set just as easily.)
After the depth-first search in line 3 is done identifying r's strongly connected component, it begins at the vertex r' with the largest finishing time of any vertex not in r's strongly connected component. Vertex r' must be its own forefather, since it can't reach anything with a higher finishing time (otherwise, it would have been included in r's strongly connected component). By similar reasoning, any vertex that can reach r' 'that is not already black must be in r''s strongly connected component. Thus, as the depth-first search in line 3 continues, it identifies and blackens every vertex in r''s strongly connected component by searching from r' in GT.
Thus, the depth-first search in line 3 "peels off" strongly connected components one by one. Each component is identified in line 7 of DFS by a call to DFS-VISIT with the forefather of the component as an argument. Recursive calls within DFS-VISIT ultimately blacken each vertex within the component. When DFS-VISIT returns to DFS, the entire component has been blackened and "peeled off." Then, DFS finds the vertex with maximum finishing time among those that have not been blackened; this vertex is the forefather of another component, and the process continues.
The following theorem formalizes this argument.
Theorem 23.17
STRONGLY-CONNECTED-COMPONENTS(G) correctly computes the strongly connected components of a directed graph G.
Proof We argue by induction on the number of depth-first trees found in the depth-first search of GT that the vertices of each tree form a strongly connected component. Each step of the inductive argument proves that a tree formed in the depth-first search of GT is a strongly connected component, assuming that all previous trees produced are strongly connected components. The basis for the induction is trivial, since for the first tree produced there are no previous trees, and hence this assumption is trivially true.
Consider a depth-first tree T with root r produced in the depth-first search of GT. Let C(r) denote the set of vertices with forefather r:
We now prove that a vertex u is placed in T if and only if u
Therefore, T contains just those vertices u for which
23.5-1
How can the number of strongly connected components of a graph change if a new edge is added?
23.5-2
Show how the procedure STRONGLY-CONNECTED-COMPONENTS works on the graph of Figure 23.6. Specifically, show the finishing times computed in line 1 and the forest produced in line 3. Assume that the loop of lines 5-7 of DFS considers vertices in alphabetical order and that the adjacency lists are in alphabetical order.
23.5-3
Professor Deaver claims that the algorithm for strongly connected components can be simplified by using the original (instead of the transpose) graph in the second depth-first search and scanning the vertices in order of increasing finishing times. Is the professor correct?
23.5-4
We denote the component graph of G = (V, E) by GSCC = (VSCC, ESCC), where VSCC contains one vertex for each strongly connected component of G and ESCC contains the edge (u, v) if there is a directed edge from a vertex in the strongly connected component of G corresponding to u to a vertex in the strongly connected component of G corresponding to v. Figure 23.9(c) shows an example. Prove that GSCC is a dag.
23.5-5
Give an O(V + E)-time algorithm to compute the component graph of a directed graph G = (V,E). Make sure that there is at most one edge between two vertices in the component graph your algorithm produces.
23.5-6
Given a directed graph G = (V, E), explain how to create another graph G' = (V, E') such that (a) G' has the same strongly connected components as G, (b) G' has the same component graph as G, and (c) E' is as small as possible. Describe a fast algorithm to compute G'.
23.5-7
A directed graph G = (V, E) is said to be semiconnected if, for any two vertices u, v
23-1 Classifying edges by breadth-first search
A depth-first forest classifies the edges of a graph into tree, back, forward, and cross edges. A breadth-first tree can also be used to classify the edges reachable from the source of the search into the same four categories.
a. Prove that in a breadth-first search of an undirected graph, the following properties hold:
1. There are no back edges and no forward edges.
2. For each tree edge (u,v), we have d[v] = d[u] + 1.
3. For each cross edge (u,v), we have d[v] = d[u] or d[v] = d[u] + 1.
b. Prove that in a breadth-first search of a directed graph, the following properties hold:
1. There are no forward edges.
2. For each tree edge (u,v), we have d[v] = d[u] + 1.
3. For each cross edge (u,v), we have d[v]
4. For each back edge (u,v), we have 0
23-2 Articulation points, bridges, and biconnected components
Let G = (V, E) be a connected, undirected graph. An articulation point of G is a vertex whose removal disconnects G. A bridge of G is an edge whose removal disconnects G. A biconnected component of G is a maximal set of edges such that any two edges in the set lie on a common simple cycle. Figure 23.10 illustrates these definitions. We can determine articulation points, bridges, and biconnected components using depth-first search. Let G
a. Prove that the root of G
b. Let v be a nonroot vertex in G
c. Let
Show how to compute low[
d. Show how to compute all articulation points in O(E) time.
e. Prove that an edge of G is a bridge if and only if it does not lie on any simple cycle of G.
f. Show how to compute all the bridges of G in O(E) time.
g. Prove that the biconnected components of G partition the nonbridge edges of G.
h. Give an O(E)-time algorithm to label each edge e of G with a positive integer bcc[e] such that bcc[e] = bcc[e'] if and only if e and e' are in the same biconnected component.
23-3 Euler tour
An Euler tour of a connected, directed graph G = (V, E) is a cycle that traverses each edge of G exactly once, although it may visit a vertex more than once.
a. Show that G has an Euler tour if and only if
in-degree(v) = out-degree(v)
for each vertex v
b. Describe an O(E)-time algorithm to find an Euler tour of G if one exists. (Hint: Merge edge-disjoint cycles.)
Even [65] and Tarjan [188] are excellent references for graph algorithms.
Breadth-first search was discovered by Moore [150] in the context of finding paths through mazes. Lee [134] independently discovered the same algorithm in the context of routing wires on circuit boards.
Hopcroft and Tarjan [102] advocated the use of the adjacency-list representation over the adjacency-matrix representation for sparse graphs and were the first to recognize the algorithmic importance of depth-first search. Depth-first search has been widely used since the late 1950's, especially in artificial intelligence programs.
Tarjan [185] gave a linear-time algorithm for finding strongly connected components. The algorithm for strongly connected components in Section 23.5 is adapted from Aho, Hopcroft, and Ullman [5], who credit it to S. R. Kosaraju and M. Sharir. Knuth [121] was the first to give a linear-time algorithm for topological sorting.
 V, the adjacency list Adj[u] contains (pointers to) all the vertices v such that there is an edge (u,v)
V, the adjacency list Adj[u] contains (pointers to) all the vertices v such that there is an edge (u,v)  E. That is, Adj[u] consists of all the vertices adjacent to u in G. The vertices in each adjacency list are typically stored in an arbitrary order. Figure 23.1(b) is an adjacency-list representation of the undirected graph in Figure 23.1(a). Similarly, Figure 23.2(b) is an adjacency-list representation of the directed graph in Figure 23.2(a).
E. That is, Adj[u] consists of all the vertices adjacent to u in G. The vertices in each adjacency list are typically stored in an arbitrary order. Figure 23.1(b) is an adjacency-list representation of the undirected graph in Figure 23.1(a). Similarly, Figure 23.2(b) is an adjacency-list representation of the directed graph in Figure 23.2(a).
Figure 23.1 Two representations of an undirected graph. (a) An undirected graph G having five vertices and seven edges. (b) An adjacency-list representation of G. (c) The adjacency-matrix representation of G.

Figure 23.2 Two representations of a directed graph. (a) A directed graph G having six vertices and eight edges. (b) An adjacency-list representation of G. (c) The adjacency-matrix representation of G.
 R. For example, let G = (V, E) be a weighted graph with weight function w. The weight w(u,v) of the edge (u,v)
R. For example, let G = (V, E) be a weighted graph with weight function w. The weight w(u,v) of the edge (u,v)  E is simply stored with vertex v in u's adjacency list. The adjacency-list representation is quite robust in that it can be modified to support many other graph variants.
E is simply stored with vertex v in u's adjacency list. The adjacency-list representation is quite robust in that it can be modified to support many other graph variants. |V| matrix A = (aij) such that
|V| matrix A = (aij) such that
 (V2) memory, independent of the number of edges in the graph.
(V2) memory, independent of the number of edges in the graph. given by
given by  . Since in an undirected graph, (u,v) and (v,u) represent the same edge, the adjacency matrix A of an undirected graph is its own transpose: A = AT. In some applications, it pays to store only the entries on and above the diagonal of the adjacency matrix, thereby cutting the memory needed to store the graph almost in half.
. Since in an undirected graph, (u,v) and (v,u) represent the same edge, the adjacency matrix A of an undirected graph is its own transpose: A = AT. In some applications, it pays to store only the entries on and above the diagonal of the adjacency matrix, thereby cutting the memory needed to store the graph almost in half. E is simply stored as the entry in row u and column v of the adjacency matrix. If an edge does not exist, a NIL value can be stored as its corresponding matrix entry, though for many problems it is convenient to use a value such as 0 or
E is simply stored as the entry in row u and column v of the adjacency matrix. If an edge does not exist, a NIL value can be stored as its corresponding matrix entry, though for many problems it is convenient to use a value such as 0 or  .
.Exercises
 V
V  V : (u,v)
V : (u,v)  E}. Thus, GT is G with all its edges reversed. Describe efficient algorithms for computing GT from G, for both the adjacency-list and adjacency-matrix representations of G. Analyze the running times of your algorithms.
E}. Thus, GT is G with all its edges reversed. Describe efficient algorithms for computing GT from G, for both the adjacency-list and adjacency-matrix representations of G. Analyze the running times of your algorithms. E2 if and only if for some v
E2 if and only if for some v  V, both (u,v)
V, both (u,v)  E and (v,w)
E and (v,w)  E. That is, G2 contains an edge between u and w whenever G contains a path with exactly two edges between u and w. Describe efficient algorithms for computing G2 from G for both the adjacency-list and adjacency-matrix representations of G. Analyze the running times of your algorithms.
E. That is, G2 contains an edge between u and w whenever G contains a path with exactly two edges between u and w. Describe efficient algorithms for computing G2 from G for both the adjacency-list and adjacency-matrix representations of G. Analyze the running times of your algorithms. (V2), but there are some exceptions. Show that determining whether a directed graph contains a sink--a vertex with in-degree |V| - 1 and out-degree 0--can be determined in time O(V), even if an adjacency-matrix representation is used.
(V2), but there are some exceptions. Show that determining whether a directed graph contains a sink--a vertex with in-degree |V| - 1 and out-degree 0--can be determined in time O(V), even if an adjacency-matrix representation is used. |E| matrix B = (bij) such that
|E| matrix B = (bij) such that
23.2 Breadth-first search
 E and vertex u is black, then vertex v is either gray or black; that is, all vertices adjacent to black vertices have been discovered. Gray vertices may have some adjacent white vertices; they represent the frontier between discovered and undiscovered vertices.
E and vertex u is black, then vertex v is either gray or black; that is, all vertices adjacent to black vertices have been discovered. Gray vertices may have some adjacent white vertices; they represent the frontier between discovered and undiscovered vertices. V is stored in the variable color[u], and the predecessor of u is stored in the variable
V is stored in the variable color[u], and the predecessor of u is stored in the variable  [u]. If u has no predecessor (for example, if u = s or u has not been discovered), then
[u]. If u has no predecessor (for example, if u = s or u has not been discovered), then  [u] = NIL. The distance from the source s to vertex u computed by the algorithm is stored in d[u]. The algorithm also uses a first-in, first-out queue Q (see Section 11.1) to manage the set of gray vertices.
[u] = NIL. The distance from the source s to vertex u computed by the algorithm is stored in d[u]. The algorithm also uses a first-in, first-out queue Q (see Section 11.1) to manage the set of gray vertices.BFS(G,s)
1 for each vertex u
 V[G] - {s}
V[G] - {s}2 do color[u]
 WHITE
WHITE3 d[u]


4
 [u]
[u]  NIL
NIL5 color[s]
 GRAY
GRAY6 d[s]
 0
07
 [s]
[s]  NIL
NIL8 Q
 {s}
{s}9 while Q


10 do u
 head[Q]
head[Q]11 for each v
 Adj[u]
Adj[u]12 do if color[v] = WHITE
13 then color[v]
 GRAY
GRAY14 d[v]
 d[u] + 1
d[u] + 115
 [v]
[v]  u
u16 ENQUEUE(Q,v)
17 DEQUEUE(Q)
18 color[u]
 BLACK
BLACK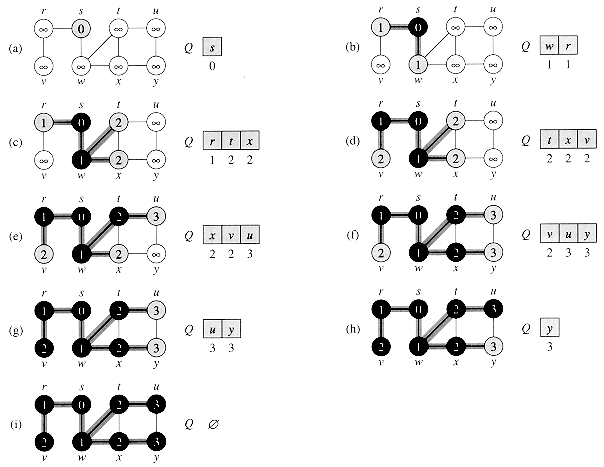
Figure 23.3 The operation of BFS on an undirected graph. Tree edges are shown shaded as they are produced by BFS. Within each vertex u is shown d[u]. The queue Q is shown at the beginning of each iteration of the while loop of lines 9-18. Vertex distances are shown next to vertices in the queue.
Analysis
 (E), at most O(E) time is spent in total scanning adjacency lists. The overhead for initialization is O(V), and thus the total running time of BFS is O(V + E). Thus, breadth-first search runs in time linear in the size of the adjacency- list representation of G.
(E), at most O(E) time is spent in total scanning adjacency lists. The overhead for initialization is O(V), and thus the total running time of BFS is O(V + E). Thus, breadth-first search runs in time linear in the size of the adjacency- list representation of G.Shortest paths
 V. Define the shortest-path distance
V. Define the shortest-path distance  (s,v) from s to v as the minimum number of edges in any path from vertex s to vertex v, or else
(s,v) from s to v as the minimum number of edges in any path from vertex s to vertex v, or else  if there is no path from s to v. A path of length
if there is no path from s to v. A path of length  (s,v) from s to v is said to be a shortest path1 from s to v. Before showing that breadth-first search actually computes shortest-path distances, we investigate an important property of shortest-path distances.
(s,v) from s to v is said to be a shortest path1 from s to v. Before showing that breadth-first search actually computes shortest-path distances, we investigate an important property of shortest-path distances. V be an arbitrary vertex. Then, for any edge (u, v)
V be an arbitrary vertex. Then, for any edge (u, v)  E,
E, (s,v)
(s,v) 
 (s,u) + 1 .
(s,u) + 1 . (s,u) =
(s,u) =  , and the inequality holds.
, and the inequality holds.  (s, v) for each vertex v
(s, v) for each vertex v  V. We first show that d [v] bounds
V. We first show that d [v] bounds  (s, v) from above.
(s, v) from above. V. Then upon termination, for each vertex v
V. Then upon termination, for each vertex v  V, the value d[v] computed by BFS satisfies d[v]
V, the value d[v] computed by BFS satisfies d[v] 
 (s, v).
(s, v).
 (s,v) for all v
(s,v) for all v  V.
V. (s, s) and d[v] =
(s, s) and d[v] = 

 (s, v) for all v
(s, v) for all v  V - {s}.
V - {s}.
 (s, u). From the assignment performed by line 14 and from Lemma 23.1, we obtain
(s, u). From the assignment performed by line 14 and from Lemma 23.1, we obtaind[v] = d[u] + 1

 (s,u) + 1
(s,u) + 1
 (s,v) .
(s,v) . (s, v), we must first show more precisely how the queue Q operates during the course of BFS. The next lemma shows that at all times, there are at most two distinct d values in the queue.
(s, v), we must first show more precisely how the queue Q operates during the course of BFS. The next lemma shows that at all times, there are at most two distinct d values in the queue. v1, v2, . . . , vr
v1, v2, . . . , vr , where v1 is the head of Q and vr is the tail. Then, d[vr]
, where v1 is the head of Q and vr is the tail. Then, d[vr]  d[v1] + 1 and d[vi]
d[v1] + 1 and d[vi]  d[vi + 1] for i = 1, 2, . . . , r - 1.
d[vi + 1] for i = 1, 2, . . . , r - 1. d[v1] + 1
d[v1] + 1  d[v2] + 1, and the remaining inequalities are unaffected. Thus, the lemma follows with v2 as the head. Enqueuing a vertex requires closer examination of the code. In line 16 of BFS, when the vertex v is enqueued, thus becoming vr+1, the head v1 of Q is in fact the vertex u whose adjacency list is currently being scanned. Thus, d[vr+1] = d[v] = d[u] + 1 = d[v1] + 1. We also have d[vr]
d[v2] + 1, and the remaining inequalities are unaffected. Thus, the lemma follows with v2 as the head. Enqueuing a vertex requires closer examination of the code. In line 16 of BFS, when the vertex v is enqueued, thus becoming vr+1, the head v1 of Q is in fact the vertex u whose adjacency list is currently being scanned. Thus, d[vr+1] = d[v] = d[u] + 1 = d[v1] + 1. We also have d[vr]  d[v1] + 1 = d[u] + 1 = d[v] = d[vr + 1], and the remaining inequalities are unaffected. Thus, the lemma follows when v is enqueued.
d[v1] + 1 = d[u] + 1 = d[v] = d[vr + 1], and the remaining inequalities are unaffected. Thus, the lemma follows when v is enqueued.  V. Then, during its execution, BFS discovers every vertex v
V. Then, during its execution, BFS discovers every vertex v  V that is reachable from the source s, and upon termination, d[v] =
V that is reachable from the source s, and upon termination, d[v] =  (s, v) for all v
(s, v) for all v  V. Moreover, for any vertex v
V. Moreover, for any vertex v  s that is reachable from s, one of the shortest paths from s to v is the shortest path from s to
s that is reachable from s, one of the shortest paths from s to v is the shortest path from s to  [v] followed by the edge (
[v] followed by the edge ( [v], v).
[v], v).
 (s, v) =
(s, v) =  , vertex v cannot have d[v] set to a finite value in line 14. By induction, there cannot be a first vertex whose d value is set to
, vertex v cannot have d[v] set to a finite value in line 14. By induction, there cannot be a first vertex whose d value is set to  by line 14. Line 14 is therefore only executed only for vertices with finite d values. Thus, if v is unreachable, it is never discovered.
by line 14. Line 14 is therefore only executed only for vertices with finite d values. Thus, if v is unreachable, it is never discovered. V :
V :  (s, v) = k}. The proof proceeds by induction on k. As an inductive hypothesis, we assume that for each vertex v
(s, v) = k}. The proof proceeds by induction on k. As an inductive hypothesis, we assume that for each vertex v  Vk, there is exactly one point during the execution of BFS at which
Vk, there is exactly one point during the execution of BFS at which v is grayed,
v is grayed, d[v] is set to k,
d[v] is set to k, if v
if v  s, then
s, then  [v] is set to u for some u
[v] is set to u for some u  Vk - 1, and
Vk - 1, and v is inserted into the queue Q.
v is inserted into the queue Q. [u] ever changes. By Lemma 23.3, therefore, if vertices are inserted into the queue over the course of the algorithm in the order v1, v2, . . . , vr, then the sequence of distances is monotonically increasing: d[vi]
[u] ever changes. By Lemma 23.3, therefore, if vertices are inserted into the queue over the course of the algorithm in the order v1, v2, . . . , vr, then the sequence of distances is monotonically increasing: d[vi]  d[vi + 1] for i = 1, 2, . . . , r - 1.
d[vi + 1] for i = 1, 2, . . . , r - 1. Vk, where k
Vk, where k  1. The monotonicity property, combined with d[v]
1. The monotonicity property, combined with d[v]  k (by Lemma 23.2) and the inductive hypothesis, implies that v must be discovered after all vertices in Vk - 1 are enqueued, if it is discovered at all.
k (by Lemma 23.2) and the inductive hypothesis, implies that v must be discovered after all vertices in Vk - 1 are enqueued, if it is discovered at all. (s, v) = k, there is a path of k edges from s to v, and thus there exists a vertex u
(s, v) = k, there is a path of k edges from s to v, and thus there exists a vertex u  Vk-1 such that (u,v)
Vk-1 such that (u,v)  E. Without loss of generality, let u be the first such vertex grayed, which must happen since, by induction, all vertices in Vk - 1 are grayed. The code for BFS enqueues every grayed vertex, and hence u must ultimately appear as the head of the queue in line 10. When u appears as the head, its adjacency list is scanned and v is discovered. (The vertex v could not have been discovered earlier, since it is not adjacent to any vertex in Vj for j < k - 1--otherwise, v could not belong to Vk--and by assumption, u is the first vertex discovered in Vk - 1 to which v is adjacent.) Line 13 grays v, line 14 establishes d[v] = d[u] + 1 = k, line 15 sets
E. Without loss of generality, let u be the first such vertex grayed, which must happen since, by induction, all vertices in Vk - 1 are grayed. The code for BFS enqueues every grayed vertex, and hence u must ultimately appear as the head of the queue in line 10. When u appears as the head, its adjacency list is scanned and v is discovered. (The vertex v could not have been discovered earlier, since it is not adjacent to any vertex in Vj for j < k - 1--otherwise, v could not belong to Vk--and by assumption, u is the first vertex discovered in Vk - 1 to which v is adjacent.) Line 13 grays v, line 14 establishes d[v] = d[u] + 1 = k, line 15 sets  [v] to u, and line 16 inserts v into the queue. Since v is an arbitrary vertex in Vk, the inductive hypothesis is proved.
[v] to u, and line 16 inserts v into the queue. Since v is an arbitrary vertex in Vk, the inductive hypothesis is proved. Vk, then by what we have just seen,
Vk, then by what we have just seen,  [v]
[v]  Vk - 1. Thus, we can obtain a shortest path from s to v by taking a shortest path from s to
Vk - 1. Thus, we can obtain a shortest path from s to v by taking a shortest path from s to  [v] and then traversing the edge (
[v] and then traversing the edge ( [v], v).
[v], v). Breadth-first trees
 field in each vertex. More formally, for a graph G = (V, E) with source s, we define the predecessor subgraph of G as G
field in each vertex. More formally, for a graph G = (V, E) with source s, we define the predecessor subgraph of G as G = (V
= (V , E
, E ), where
), whereV
 = {v
= {v  V :
V :  [v]
[v]  NIL}
NIL}  {s}
{s}E
 = {(
= {( [v],v)
[v],v)  E : v
E : v  V
V - {s}} .
- {s}} . is a breadth-first tree if V
is a breadth-first tree if V consists of the vertices reachable from s and, for all v
consists of the vertices reachable from s and, for all v  V
V , there is a unique simple path from s to v in G
, there is a unique simple path from s to v in G that is also a shortest path from s to v in G. A breadth-first tree is in fact a tree, since it is connected and |E
that is also a shortest path from s to v in G. A breadth-first tree is in fact a tree, since it is connected and |E | = |V
| = |V | - 1 (see Theorem 5.2). The edges in E
| - 1 (see Theorem 5.2). The edges in E are called tree edges.
are called tree edges. so that the predecessor subgraph G
so that the predecessor subgraph G = (V
= (V , E
, E ) is a breadth-first tree.
) is a breadth-first tree. [v] = u if (u, v)
[v] = u if (u, v)  E and
E and  (s, v) <
(s, v) <  --that is, if v is reachable from s--and thus V
--that is, if v is reachable from s--and thus V consists of the vertices in V reachable from v. Since G
consists of the vertices in V reachable from v. Since G forms a tree, it contains a unique path from s to each vertex in V
forms a tree, it contains a unique path from s to each vertex in V . By applying Theorem 23.4 inductively, we conclude that every such path is a shortest path.
. By applying Theorem 23.4 inductively, we conclude that every such path is a shortest path. PRINT-PATH(G,s,v)
1 if v = s
2 then print s
3 else if
 [v] = NIL
[v] = NIL4 then print "no path from" s "to" v "exists"
5 else PRINT-PATH(G,s,
 [v])
[v])6 print v
Exercises
 V, and a set of tree edges E
V, and a set of tree edges E
 E such that for each vertex v
E such that for each vertex v  V, the unique path in E
V, the unique path in E from s to v is a shortest path in G, yet the set of edges E
from s to v is a shortest path in G, yet the set of edges E cannot be produced by running BFS on G, no matter how the vertices are ordered in each adjacency list.
cannot be produced by running BFS on G, no matter how the vertices are ordered in each adjacency list.
23.3 Depth-first search
 [v] to u. Unlike breadth-first search, whose predecessor subgraph forms a tree, the predecessor subgraph produced by a depth-first search may be composed of several trees, because the search may be repeated from multiple sources. The predecessor subgraph of a depth-first search is therefore defined slightly differently from that of a breadth-first search: we let G
[v] to u. Unlike breadth-first search, whose predecessor subgraph forms a tree, the predecessor subgraph produced by a depth-first search may be composed of several trees, because the search may be repeated from multiple sources. The predecessor subgraph of a depth-first search is therefore defined slightly differently from that of a breadth-first search: we let G = (V, E
= (V, E ), where
), whereE
 = {(
= {( [v], v) : v
[v], v) : v  V and
V and  [v]
[v]  NIL} .
NIL} . are called tree edges.
are called tree edges.d[u] < f[u] .
(23.1)
DFS(G)
1 for each vertex u
 V[G]
V[G]2 do color[u]
 WHITE
WHITE3
 [u]
[u]  NIL
NIL4 time
 0
05 for each vertex u
 V[G]
V[G]6 do if color[u] = WHITE
7 then DFS-VISIT(u)

 fields to NIL. Line 4 resets the global time counter. Lines 5-7 check each vertex in V in turn and, when a white vertex is found, visit it using DFS-VISIT. Every time DFS-VISIT(u) is called in line 7, vertex u becomes the root of a new tree in the depth-first forest. When DFS returns, every vertex u has been assigned a discovery time d[u] and a finishing time â[u].
fields to NIL. Line 4 resets the global time counter. Lines 5-7 check each vertex in V in turn and, when a white vertex is found, visit it using DFS-VISIT. Every time DFS-VISIT(u) is called in line 7, vertex u becomes the root of a new tree in the depth-first forest. When DFS returns, every vertex u has been assigned a discovery time d[u] and a finishing time â[u]. Adj[u] is considered in line 3, we say that edge (u, v) is explored by the depth-first search. Finally, after every edge leaving u has been explored, lines 7-8 paint u black and record the finishing time in â[u].
Adj[u] is considered in line 3, we say that edge (u, v) is explored by the depth-first search. Finally, after every edge leaving u has been explored, lines 7-8 paint u black and record the finishing time in â[u].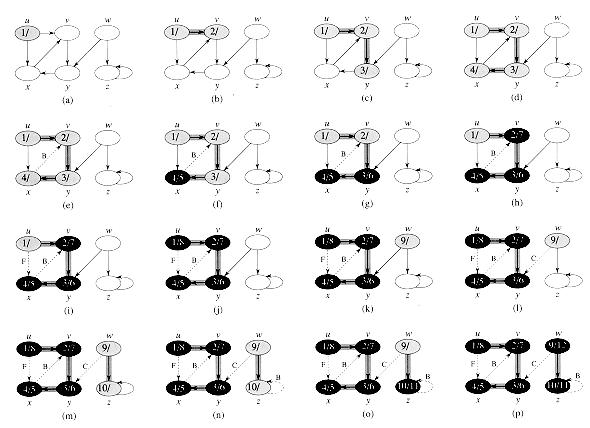
Figure 23.4 The progress of the depth-first-search algorithm DFS on a directed graph. As edges are explored by the algorithm, they are shown as either shaded (if they are tree edges) or dashed (otherwise). Nontree edges are labeled B, C, or F according to whether they are back, cross, or forward edges. Vertices are timestamped by discovery time/finishing time.
 (V), exclusive of the time to execute the calls to DFS-VISIT. The procedure DFS-VISIT is called exactly once for each vertex the v
(V), exclusive of the time to execute the calls to DFS-VISIT. The procedure DFS-VISIT is called exactly once for each vertex the v  V, since DFS-VISIT is invoked only on white vertices and the first thing it does is paint the vertex gray. During an execution of DFS-VISIT(v), the loop on lines 3-6 is executed |Adj[v]| times. Since
V, since DFS-VISIT is invoked only on white vertices and the first thing it does is paint the vertex gray. During an execution of DFS-VISIT(v), the loop on lines 3-6 is executed |Adj[v]| times. Since
 (E). The running time of DFS is therefore
(E). The running time of DFS is therefore  (V + E).
(V + E).Properties of depth-first search
 does indeed form a forest of trees, since the structure of the depth-first trees exactly mirrors the structure of recursive calls of DFS-VISIT. That is, u =
does indeed form a forest of trees, since the structure of the depth-first trees exactly mirrors the structure of recursive calls of DFS-VISIT. That is, u =  [v] if and only if DFS-VISIT (v) was called during a search of u's adjacency list.
[v] if and only if DFS-VISIT (v) was called during a search of u's adjacency list. the intervals [d[u], â[u]] and [d[v], â[v]] are entirely disjoint,
the intervals [d[u], â[u]] and [d[v], â[v]] are entirely disjoint, the interval [d[u], â[u]] is contained entirely within the interval [d[v], â[u]], and u is a descendant of v in the depth-first tree, or
the interval [d[u], â[u]] is contained entirely within the interval [d[v], â[u]], and u is a descendant of v in the depth-first tree, or the interval [d[v], â[v]] is contained entirely within the interval [d[u], â[u]], and v is a descendant of u in the depth-first tree.
the interval [d[v], â[v]] is contained entirely within the interval [d[u], â[u]], and v is a descendant of u in the depth-first tree.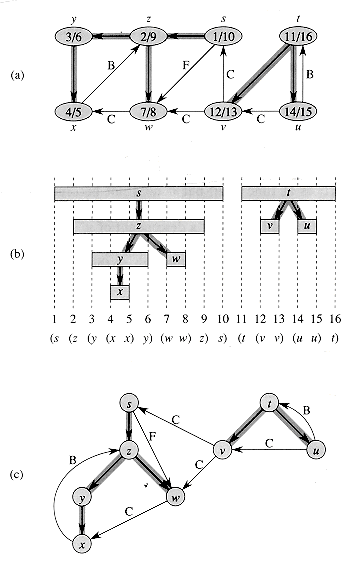
Figure 23.5 Properties of depth-first search. (a) The result of a depth-first search of a directed graph. Vertices are timestamped and edge types are indicated as in Figure 23.4. (b) Intervals for the discovery time and finishing time of each vertex correspond to the parenthesization shown. Each rectangle spans the interval given by the discovery and finishing times of the corresponding vertex. Tree edges are shown. If two intervals overlap, then one is nested within the other, and the vertex corresponding to the smaller interval is a descendant of the vertex corresponding to the larger. (c) The graph of part (a) redrawn with all tree and forward edges going down within a depth-first tree and all back edges going up from a descendant to an ancestor.
 : Assume that v is a descendant of u. Let w be any vertex on the path between u and v in the depth-first tree, so that w is a descendant of u. By Corollary 23.7, d[u] < d[w], and so w is white at time d[u].
: Assume that v is a descendant of u. Let w be any vertex on the path between u and v in the depth-first tree, so that w is a descendant of u. By Corollary 23.7, d[u] < d[w], and so w is white at time d[u]. : Suppose that vertex v is reachable from u along a path of white vertices at time d[u], but v does not become a descendant of u in the depth-first tree. Without loss of generality, assume that every other vertex along the path becomes a descendant of u. (Otherwise, let v be the closest vertex to u along the path that doesn't become a descendant of u.) Let w be the predecessor of v in the path, so that w is a descendant of u (w and u may in fact be the same vertex) and, by Corollary 23.7, â[w]
: Suppose that vertex v is reachable from u along a path of white vertices at time d[u], but v does not become a descendant of u in the depth-first tree. Without loss of generality, assume that every other vertex along the path becomes a descendant of u. (Otherwise, let v be the closest vertex to u along the path that doesn't become a descendant of u.) Let w be the predecessor of v in the path, so that w is a descendant of u (w and u may in fact be the same vertex) and, by Corollary 23.7, â[w]  â[u]. Note that v must be discovered after u is discovered, but before w is finished. Therefore, d[u] < d[v] < â[w] <â[u]. Theorem 23.6 then implies that the interval [d[v], â[v]] is contained entirely within the interval [d[u],â[u]]. By Corollary 23.7, v must after all be a descendant of u.
â[u]. Note that v must be discovered after u is discovered, but before w is finished. Therefore, d[u] < d[v] < â[w] <â[u]. Theorem 23.6 then implies that the interval [d[v], â[v]] is contained entirely within the interval [d[u],â[u]]. By Corollary 23.7, v must after all be a descendant of u. Classification of edges
 produced by a depth-first search on G.
produced by a depth-first search on G. . Edge (u, v) is a tree edge if v was first discovered by exploring edge (u, v).
. Edge (u, v) is a tree edge if v was first discovered by exploring edge (u, v).Exercises

Figure 23.6 A directed graph for use in Exercises 23.3-2 and 23.5-2.
 implies that there is at most one simple path from u to v for all vertices u, v
implies that there is at most one simple path from u to v for all vertices u, v  V. Give an efficient algorithm to determine whether or not a directed graph is singly connected.
V. Give an efficient algorithm to determine whether or not a directed graph is singly connected.23.4 Topological sort
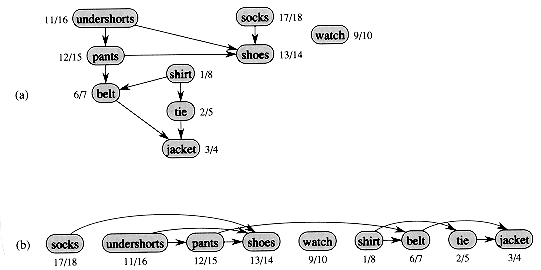
Figure 23.7 (a) Professor Bumstead topologically sorts his clothing when getting dressed. Each directed edge (u,v) means that garment u must be put on before garment v. The discovery and finishing times from a depth-first search are shown next to each vertex. (b) The same graph shown topologically sorted. Its vertices are arranged from left to right in order of decreasing finishing time. Note that all directed edges go from left to right.
TOPOLOGICAL-SORT(G)
1 call DFS(G) to compute finishing times f[v] for each vertex v
2 as each vertex is finished, insert it onto the front of a linked list
3 return the linked list of vertices
 (V + E), since depth-first search takes
(V + E), since depth-first search takes  (V + E) time and it takes 0(1) time to insert each of the |V| vertices onto the front of the linked list.
(V + E) time and it takes 0(1) time to insert each of the |V| vertices onto the front of the linked list. : Suppose that there is a back edge (u, v). Then, vertex v is an ancestor of vertex u in the depth-first forest. There is thus a path from v to u in G, and the back edge (u, v) completes a cycle.
: Suppose that there is a back edge (u, v). Then, vertex v is an ancestor of vertex u in the depth-first forest. There is thus a path from v to u in G, and the back edge (u, v) completes a cycle.
Figure 23.8 A dag for topological sorting.
 : Suppose that G contains a cycle c. We show that a depth-first search of G yields a back edge. Let v be the first vertex to be discovered in c, and let (u, v) be the preceding edge in c. At time d[v], there is a path of white vertices from v to u. By the white-path theorem, vertex u becomes a descendant of v in the depth-first forest. Therefore, (u, v) is a back edge.
: Suppose that G contains a cycle c. We show that a depth-first search of G yields a back edge. Let v be the first vertex to be discovered in c, and let (u, v) be the preceding edge in c. At time d[v], there is a path of white vertices from v to u. By the white-path theorem, vertex u becomes a descendant of v in the depth-first forest. Therefore, (u, v) is a back edge.  V, if there is an edge in G from u to v, then f[v] < f[u]. Consider any edge (u,v) explored by DFS(G). When this edge is explored, v cannot be gray, since then v would be an ancestor of u and (u,v) would be a back edge, contradicting Lemma 23.10. Therefore, v must be either white or black. If v is white, it becomes a descendant of u, and so f[v] < f[u]. If v is black, then f[v] < f[u] as well. Thus, for any edge (u,v) in the dag, we have f[v] < f[u], proving the theorem.
V, if there is an edge in G from u to v, then f[v] < f[u]. Consider any edge (u,v) explored by DFS(G). When this edge is explored, v cannot be gray, since then v would be an ancestor of u and (u,v) would be a back edge, contradicting Lemma 23.10. Therefore, v must be either white or black. If v is white, it becomes a descendant of u, and so f[v] < f[u]. If v is black, then f[v] < f[u] as well. Thus, for any edge (u,v) in the dag, we have f[v] < f[u], proving the theorem. Exercises
23.5 Strongly connected components
 V such that for every pair of vertices u and v in U, we have both
V such that for every pair of vertices u and v in U, we have both  that is, vertices u and v are reachable from each other. Figure 23.9 shows an example.
that is, vertices u and v are reachable from each other. Figure 23.9 shows an example. E}. That is, ET consists of the edges of G with their directions reversed. Given an adjacency-list representation of G, the time to create GT is O(V + E). It is interesting to observe that G and GT have exactly the same strongly connected components: u and v are reachable from each other in G if and only if they are reachable from each other in GT. Figure 23.9(b) shows the transpose of the graph in Figure 23.9(a), with the strongly connected components shaded.
E}. That is, ET consists of the edges of G with their directions reversed. Given an adjacency-list representation of G, the time to create GT is O(V + E). It is interesting to observe that G and GT have exactly the same strongly connected components: u and v are reachable from each other in G if and only if they are reachable from each other in GT. Figure 23.9(b) shows the transpose of the graph in Figure 23.9(a), with the strongly connected components shaded.
Figure 23.9 (a) A directed graph G. The strongly connected components of G are shown as shaded regions. Each vertex is labeled with its discovery and finishing times. Tree edges are shaded. (b) The graph GT, the transpose of G. The depth-first tree computed in line 3 of STRONGLY-CONNECTED-COMPONENTS is shown, with tree edges shaded. Each strongly connected component corresponds to one depth-first tree. Vertices b, c, g, and h, which are heavily shaded, are forefathers of every vertex in their strongly connected component; these vertices are also the roots of the depth-first trees produced by the depth-first search of GT. (c) The acyclic component graph Gscc obtained by shrinking each strongly connected component of G to a single vertex.
 (V + E)-time) algorithm computes the strongly connected components of a directed graph G = (V, E) using two depth-first searches, one on G and one on GT.
(V + E)-time) algorithm computes the strongly connected components of a directed graph G = (V, E) using two depth-first searches, one on G and one on GT.STRONGLY-CONNECTED-COMPONENTS(G)
1 call DFS(G) to compute finishing times f[u] for each vertex u
2 compute GT
3 call DFS(GT), but in the main loop of DFS, consider the vertices
in order of decreasing f[u] (as computed in line 1)
4 output the vertices of each tree in the depth-first forest of step 3 as a
separate strongly connected component
 , so that w is reachable from u. Moreover, since there is a path
, so that w is reachable from u. Moreover, since there is a path  , we know that u is reachable from w by the path
, we know that u is reachable from w by the path  . Therefore, u and w are in the same strongly connected component. Since w was chosen arbitrarily, the theorem is proved.
. Therefore, u and w are in the same strongly connected component. Since w was chosen arbitrarily, the theorem is proved.  refers to the existence of a path in G, not in GT.
refers to the existence of a path in G, not in GT. (u) of a vertex u, which is the vertex w reachable from u that finished last in the depth-first search of line l. In other words,
(u) of a vertex u, which is the vertex w reachable from u that finished last in the depth-first search of line l. In other words, (u) = that vertex w such that
(u) = that vertex w such that  and f[w] is maximized .
and f[w] is maximized . (u) = u is possible because u is reachable from itself, and hence
(u) = u is possible because u is reachable from itself, and hencef[u]
 f[
f[ (u)] .
(u)] .(23.2)
 (
( (u)) =
(u)) =  (u), by the following reasoning. For any vertices u, v
(u), by the following reasoning. For any vertices u, v  V,
V,
(23.3)
 and the forefather has the maximum finishing time of all reachable vertices. Since
and the forefather has the maximum finishing time of all reachable vertices. Since  (u) is reachable from u, formula (23.3) implies that f[
(u) is reachable from u, formula (23.3) implies that f[ (
( (u))]
(u))]  f[
f[ (u)]. We also have f[
(u)]. We also have f[ (u)]
(u)]  f[
f[ (
( (u))], by inequality (23.2). Thus, f[
(u))], by inequality (23.2). Thus, f[ (
( (u))] = f[
(u))] = f[ (u)], and so we have
(u)], and so we have  (
( (u)) =
(u)) =  (u), since two vertices that finish at the same time are in fact the same vertex.
(u), since two vertices that finish at the same time are in fact the same vertex. (u) of any vertex u
(u) of any vertex u  V in any depth-first search of G is an ancestor of u.
V in any depth-first search of G is an ancestor of u. (u) = u, the theorem is trivially true. If
(u) = u, the theorem is trivially true. If  (u)
(u)  u, consider the colors of the vertices at time d[u]. If
u, consider the colors of the vertices at time d[u]. If  (u) is black, then f[
(u) is black, then f[ (u)] < f[u], contradicting inequality (23.2). If
(u)] < f[u], contradicting inequality (23.2). If  (u) is gray, then it is an ancestor of u, and the theorem is proved.
(u) is gray, then it is an ancestor of u, and the theorem is proved. (u) is not white. There are two cases, according to the colors of the intermediate vertices, if any, on the path from u to
(u) is not white. There are two cases, according to the colors of the intermediate vertices, if any, on the path from u to  (u).
(u). (u) becomes a descendant of u, by the white-path theorem. But then f[
(u) becomes a descendant of u, by the white-path theorem. But then f[ (u)] < f[u], contradicting inequality (23.2).
(u)] < f[u], contradicting inequality (23.2). (u). Then, t must be gray, since there is never an edge from a black vertex to a white vertex, and t's successor is white. But then there is a path of white vertices from t to
(u). Then, t must be gray, since there is never an edge from a black vertex to a white vertex, and t's successor is white. But then there is a path of white vertices from t to  (u), and so
(u), and so  (u) is a descendant of t by the white-path theorem. This implies that f[t] > f[
(u) is a descendant of t by the white-path theorem. This implies that f[t] > f[ (u)], contradicting our choice of
(u)], contradicting our choice of  (u), since there is a path from u to t.
(u), since there is a path from u to t.  V, lie in the same strongly connected component.
V, lie in the same strongly connected component. , by the definition of forefather, and
, by the definition of forefather, and  since ø(u) is an ancestor of u.
since ø(u) is an ancestor of u.  V lie in the same strongly connected component if and only if they have the same forefather in a depth-first search of G.
V lie in the same strongly connected component if and only if they have the same forefather in a depth-first search of G. : Assume that u and v are in the same strongly connected component. Every vertex reachable from u is reachable from v and vice versa, since there are paths in both directions between u and v. By the definition of forefather, then, we conclude that
: Assume that u and v are in the same strongly connected component. Every vertex reachable from u is reachable from v and vice versa, since there are paths in both directions between u and v. By the definition of forefather, then, we conclude that  (u) =
(u) =  (v).
(v). : Assume that
: Assume that  (u) =
(u) =  (v). By Corollary 23.15, u is in the same strongly connected component as
(v). By Corollary 23.15, u is in the same strongly connected component as  (u), and v is in the same strongly connected component as
(u), and v is in the same strongly connected component as  (v). Therefore, u and v are in the same strongly connected component.
(v). Therefore, u and v are in the same strongly connected component. C(r) = {v  V:
V:  (v) = r}.
(v) = r}. C(r).
C(r). : Theorem 23.13 implies that every vertex in C(r) ends up in the same depth-first tree. Since r
: Theorem 23.13 implies that every vertex in C(r) ends up in the same depth-first tree. Since r  C(r) and r is the root of T, every element of C(r) ends up in T.
C(r) and r is the root of T, every element of C(r) ends up in T. : We show that any vertex w such that â[
: We show that any vertex w such that â[ (w)] > â[r] or â[
(w)] > â[r] or â[ (w)] < â[r] is not placed in T, by considering these two cases separately. By induction on the number of trees found, any vertex w such that â[
(w)] < â[r] is not placed in T, by considering these two cases separately. By induction on the number of trees found, any vertex w such that â[ (w)] > â[r] is not placed in tree T, since at the time r is selected w will have already been placed in the tree with root
(w)] > â[r] is not placed in tree T, since at the time r is selected w will have already been placed in the tree with root  (w). Any vertex w such that â[
(w). Any vertex w such that â[ (w)] < â[r] cannot be placed in T, since such a placement would imply
(w)] < â[r] cannot be placed in T, since such a placement would imply  ; thus, by formula (23.3) and the property that r =
; thus, by formula (23.3) and the property that r =  (r), we obtain â[
(r), we obtain â[ (w)]
(w)]  â[
â[ (r)] = â[r], which contradicts â[
(r)] = â[r], which contradicts â[ (w)] < â[r].
(w)] < â[r]. (u) = r. That is, T is exactly equal to the strongly connected component C(r), which completes the inductive proof.
(u) = r. That is, T is exactly equal to the strongly connected component C(r), which completes the inductive proof. Exercises
 V, we have
V, we have  . Give an efficient algorithm to determine whether or not G is semiconnected. Prove that your algorithm is correct, and analyze its running time.
. Give an efficient algorithm to determine whether or not G is semiconnected. Prove that your algorithm is correct, and analyze its running time.Problems
 d[u] + 1.
d[u] + 1. d[v] < d[u].
d[v] < d[u]. = (V,E
= (V,E ) be a depth-first tree of G.
) be a depth-first tree of G.
Figure 23.10 The articulation points, bridges, and biconnected components of a connected, undirected graph for use in Problem 23-2. The articulation points are the heavily shaded vertices, the bridges are the heavily shaded edges, and the biconnected components are the edges in the shaded regions, with a bcc numbering shown.
 is an articulation point of G if and only if it has at least two children in G
is an articulation point of G if and only if it has at least two children in G .
. . Prove that v is an articulation point of G if and only if there is no back edge (u, w) such that in G
. Prove that v is an articulation point of G if and only if there is no back edge (u, w) such that in G , u is a descendant of
, u is a descendant of  and w is a proper ancestor of v.
and w is a proper ancestor of v.
 ] for all vertices
] for all vertices 
 V in O(E) time.
V in O(E) time. V.
V.Chapter notes


