Comparison networks differ from RAM's in two important respects. First, they can only perform comparisons. Thus, an algorithm such as counting sort (see Section 9.2) cannot be implemented on a comparison network. Second, unlike the RAM model, in which operations occur serially--that is, one after another--operations in a comparison network may occur at the same time, or "in parallel." As we shall see, this characteristic allows the construction of comparison networks that sort n values in sublinear time.
We begin in Section 28.1 by defining comparison networks and sorting networks. We also give a natural definition for the "running time" of a comparison network in terms of the depth of the network. Section 28.2 proves the "zero-one principle," which greatly eases the task of analyzing the correctness of sorting networks.
The efficient sorting network that we shall design is essentially a parallel version of the merge-sort algorithm from Section 1.3.1. Our construction will have three steps. Section 28.3 presents the design of a "bitonic" sorter that will be our basic building block. We modify the bitonic sorter slightly in Section 28.4 to produce a merging network that can merge two sorted sequences into one sorted sequence. Finally, in Section 28.5, we assemble these merging networks into a sorting network that can sort n values in O(lg2 n) time.
28.1 Comparison networks
Sorting networks are comparison networks that always sort their inputs, so it makes sense to begin our discussion with comparison networks and their characteristics. A comparison network is comprised solely of wires and comparators. A comparator, shown in Figure 28.1 (a), is a device with two inputs, x and y, and two outputs, x' and y', that performs the following function:
Because the pictorial representation of a comparator in Figure 28.1 (a) is too bulky for our purposes, we shall adopt the convention of drawing comparators as single vertical lines, as shown in Figure 28.1(b). Inputs appear on the left and outputs on the right, with the smaller input value appearing on the top output and the larger input value appearing on the bottom output. We can thus think of a comparator as sorting its two inputs.
We shall assume that each comparator operates in O(1) time. In other words, we assume that the time between the appearance of the input values x and y and the production of the output values x' and y' is a constant.
A wire transmits a value from place to place. Wires can connect the output of one comparator to the input of another, but otherwise they are either network input wires or network output wires. Throughout this chapter, we shall assume that a comparison network contains n input wires a1, a2, . . . , an, through which the values to be sorted enter the network, and n output wires b1, b2, . . . , bn, which produce the results computed by the network. Also, we shall speak of the input sequence
Figure 28.2 shows a comparison network, which is a set of comparators interconnected by wires. We draw a comparison network on n inputs as a collection of n horizontal lines with comparators stretched vertically. Note that a line does not represent a single wire, but rather a sequence of distinct wires connecting various comparators. The top line in Figure 28.2, for example, represents three wires: input wire a1, which connects to an input of comparator A; a wire connecting the top output of comparator A to an input of comparator C; and output wire b1, which comes from the top output of comparator C. Each comparator input is connected to a wire that is either one of the network's n input wires a1, a2, . . . , an or is connected to the output of another comparator. Similarly, each comparator output is connected to a wire that is either one of the network's n output wires b1, b2, . . . , bn or is connected to the input of another comparator. The main requirement for interconnecting comparators is that the graph of interconnections must be acyclic: if we trace a path from the output of a given comparator to the input of another to output to input, etc., the path we trace must never cycle back on itself and go through the same comparator twice. Thus, as in Figure 28.2, we can draw a comparison network with network inputs on the left and network outputs on the right; data move through the network from left to right.
Each comparator produces its output values only when both of its input values are available to it. In Figure 28.2(a), for example, suppose that the sequence
Under the assumption that each comparator takes unit time, we can define the "running time" of a comparison network, that is, the time it takes for all the output wires to receive their values once the input wires receive theirs. Informally, this time is the largest number of comparators that any input element can pass through as it travels from an input wire to an output wire. More formally, we define the depth of a wire as follows. An input wire of a comparison network has depth 0. Now, if a comparator has two input wires with depths dx and dy, then its output wires have depth max(dx, dy) + 1. Because there are no cycles of comparators in a comparison network, the depth of a wire is well defined, and we define the depth of a comparator to be the depth of its output wires. Figure 28.2 shows comparator depths. The depth of a comparison network is the maximum depth of an output wire or, equivalently, the maximum depth of a comparator. The comparison network of Figure 28.2, for example, has depth 3 because comparator E has depth 3. If each comparator takes one time unit to produce its output value, and if network inputs appear at time 0, a comparator at depth d produces its outputs at time d; the depth of the network therefore equals the time for the network to produce values at all of its output wires.
A sorting network is a comparison network for which the output sequence is monotonically increasing (that is, b1
A comparison network is like a procedure in that it specifies how comparisons are to occur, but it is unlike a procedure in that its physical size depends on the number of inputs and outputs. Therefore, we shall actually be describing "families" of comparison networks. For example, the goal of this chapter is to develop a family SORTER of efficient sorting networks. We specify a given network within a family by the family name and the number of inputs (which equals the number of outputs). For example, the n-input, n-output sorting network in the family SORTER is named SORTER[n].
28.1-1
Show the values that appear on all the wires of the network of Figure 28.2 when it is given the input sequence
28.1-2
Let n be an exact power of 2. Show how to construct an n-input, n-output comparison network of depth lg n in which the top output wire always carries the minimum input value and the bottom output wire always carries the maximum input value.
28.1-3
Professor Nielsen claims that if we add a comparator anywhere in a sorting network, the resulting network also sorts. Show that the professor is mistaken by adding a comparator to the network of Figure 28.2 in such a way that the resulting network does not sort every input permutation.
28.1-4
Prove that any sorting network on n inputs has depth at least lg n.
28.1-5
Prove that the number of comparators in any sorting network is at least
28.1-6
Consider the comparison network shown in Figure 28.3. Prove that it is in fact a sorting network, and describe how its structure is related to that of insertion sort (Section 1.1).
28.1-7
We can represent an n-input comparison network with c comparators as a list of c pairs of integers in the range from 1 to n. If two pairs contain an integer in common, the order of the corresponding comparators in the network is determined by the order of the pairs in the list. Given this representation, describe an O(n+c)-time (serial) algorithm for determining the depth of a comparison network.
28.1-8
Suppose that in addition to the standard kind of comparator, we introduce an "upside-down" comparator that produces its minimum output on the bottom wire and its maximum output on the top wire. Show how to convert any sorting network that uses a total of c standard and upside-down comparators to one that uses c standard ones. Prove that your conversion method is correct.
The zero-one principle says that if a sorting network works correctly when each input is drawn from the set {0,1}, then it works correctly on arbitrary input numbers. (The numbers can be integers, reals, or, in general, any set of values from any linearly ordered set.) As we construct sorting networks and other comparison networks, the zero-one principle will allow us to focus on their operation for input sequences consisting solely of 0's and 1's. Once we have constructed a sorting network and proved that it can sort all zero-one sequences, we shall appeal to the zero-one principle to show that it properly sorts sequences of arbitrary values.
The proof of the zero-one principle relies on the notion of a monotonically increasing function (Section 2.2).
Lemma 28.1
If a comparison network transforms the input sequence a =
Proof We shall first prove the claim that if f is a monotonically increasing function, then a single comparator with inputs f(x) and f(y) produces outputs f(min(x,y)) and f(max(x,y)). We shall then use induction to prove the lemma.
To prove the claim, consider a comparator whose input values are x and y. The upper output of the comparator is min(x,y) and the lower output is max(x,y). Suppose we now apply f(x) and f(y) to the inputs of the comparator, as is shown in Figure 28.4. The operation of the comparator yields the value min(f(x), f(y)) on the upper output and the value max(f(x), f(y)) on the lower output. Since f is monotonically increasing, x
Thus, the comparator produces the values f (min(x,y)) and f (max(x,y)) when f (x) and f (y) are its inputs, which completes the proof of the claim.
We can use induction on the depth of each wire in a general comparison network to prove a stronger result than the statement of the lemma: if a wire assumes the value ai when the input sequence a is applied to the network, then it assumes the value f(ai) when the input sequence f(a) is applied. Because the output wires are included in this statement, proving it will prove the lemma.
For the basis, consider a wire at depth 0, that is, an input wire ai. The result follows trivially: when f(a) is applied to the network, the input wire carries f(ai). For the inductive step, consider a wire at depth d, where d
As an example of the application of Lemma 28.1, Figure 28.5 shows the sorting network from Figure 28.2 with the monotonically increasing function f(x) =
When a comparison network is a sorting network, Lemma 28.1 allows us to prove the following remarkable result.
Theorem 28.2
If a comparison network with n inputs sorts all 2n possible sequences of 0's and 1's correctly, then it sorts all sequences of arbitrary numbers correctly.
Proof Suppose for the purpose of contradiction that the network sorts all zero-one sequences, but there exists a sequence of arbitrary numbers that the network does not correctly sort. That is, there exists an input sequence
Since the network places aj before ai in the output sequence when
28.2-1
Prove that applying a monotonically increasing function to a sorted sequence produces a sorted sequence.
28.2-2
Prove that a comparison network with n inputs correctly sorts the input sequence
28.2-3
Use the zero-one principle to prove that the comparison network shown in Figure 28.6 is a sorting network.
28.2-4
State and prove an analog of the zero-one principle for a decision-tree model. (Hint: Be sure to handle equality properly.)
28.2-5
Prove that an n-input sorting network must contain at least one comparator between the ith and (i + 1 )st lines for all i = 1, 2, . . . , n - 1.
The first step in our construction of an efficient sorting network is to construct a comparison network that can sort any bitonic sequence: a sequence that either monotonically increases and then monotonically decreases, or else monotonically decreases and then monotonically increases. For example, the sequences
The bitonic sorter that we shall construct is a comparison network that sorts bitonic sequences of 0's and 1's. Exercise 28.3-6 asks you to show that the bitonic sorter can sort bitonic sequences of arbitrary numbers.
A bitonic sorter is comprised of several stages, each of which is called a half-cleaner. Each half-cleaner is a comparison network of depth 1 in which input line i is compared with line i + n/2 for i = 1, 2, . . . , n/2. (We assume that n is even.) Figure 28.7 shows HALF-CLEANER[8], the half-cleaner with 8 inputs and 8 outputs.
When a bitonic sequence of 0's and 1's is applied as input to a half-cleaner, the half-cleaner produces an output sequence in which smaller values are in the top half, larger values are in the bottom half, and both halves are bitonic. In fact, at least one of the halves is clean--consisting of either all 0's or all 1's--and it is from this property that we derive the name "half-cleaner." (Note that all clean sequences are bitonic.) The next lemma proves these properties of half-cleaners.
Lemma 28.3
If the input to a half-cleaner is a bitonic sequence of 0's and 1's, then the output satisfies the following properties: both the top half and the bottom half are bitonic, every element in the top half is at least as small as every element of the bottom half, and at least one half is clean.
Proof The comparison network HALF-CLEANER[n] compares inputs i and i + n/2 for i = 1, 2, . . . , n/2. Without loss of generality, suppose that the input is of the form 00 . . . 011 . . . 100 . . . 0. (The situation in which the input is of the form 11 . . . 100 . . . 011 . . . 1 is symmetric.) There are three possible cases depending upon the block of consecutive 0's or 1s in which the midpoint n/2 falls, and one of these cases (the one in which the midpoint occurs in the block of 1's) is further split into two cases. The four cases are shown in Figure 28.8. In each case shown, the lemma holds.
By recursively combining half-cleaners, as shown in Figure 28.9, we can build a bitonic sorter, which is a network that sorts bitonic sequences. The first stage of BITONIC-SORTER[n] consists of HALF-CLEANER[n], which, by Lemma 28.3, produces two bitonic sequences of half the size such that every element in the top half is at least as small as every element in the bottom half. Thus, we can complete the sort by using two copies of BITONIC-SORTER[n/2] to sort the two halves recursively. In Figure 28.9(a), the recursion has been shown explicitly, and in Figure 28.9(b), the recursion has been unrolled to show the progressively smaller half-cleaners that make up the remainder of the bitonic sorter. The depth D(n) of BITONIC-SORTER[n] is given by the recurrence whose solution is D(n) = lg n.
Thus, a zero-one bitonic sequence can be sorted by BITONIC-SORTER, which has a depth of lg n. It follows by the analog of the zero-one principle given as Exercise 28.3-6 that any bitonic sequence of arbitrary numbers can be sorted by this network.
28.3-1
How many bitonic sequences of 0's and 1's are there?
28.3-2
Show that BITONIC-SORTER[n], where n is an exact power of 2, contains
28.3-3
Describe how an O(lg n)-depth bitonic sorter can be constructed when the number n of inputs is not an exact power of 2.
28.3-4
If the input to a half-cleaner is a bitonic sequence of arbitrary numbers, prove that the output satisfies the following properties: both the top half and the bottom half are bitonic, and every element in the top half is at least as small as every element in the bottom half.
28.3-5
Consider two sequences of 0's and 1's. Prove that if every element in one sequence is at least as small as every element in the other sequence, then one of the two sequences is clean.
28.3-6
Prove the following analog of the zero-one principle for bitonic sorting networks: a comparison network that can sort any bitonic sequence of 0's and 1's can sort any bitonic sequence of arbitrary numbers.
Our sorting network will be constructed from merging networks, which are networks that can merge two sorted input sequences into one sorted output sequence. We modify BITONIC-SORTER[n] to create the merging network MERGER[n]. As with the bitonic sorter, we shall prove the correctness of the merging network only for inputs that are zero-one sequences. Exercise 28.4-1 asks you to show how the proof can be extended to arbitrary input values.
The merging network is based on the following intuition. Given two sorted sequences, if we reverse the order of the second sequence and then concatenate the two sequences, the resulting sequence is bitonic. For example, given the sorted zero-one sequences X = 00000111 and Y = 00001111, we reverse Y to get YR = 11110000. Concatenating X and YR yields 0000011111110000, which is bitonic. Thus, to merge the two input sequences X and Y, it suffices to perform a bitonic sort on X concatenated with YR.
We can construct MERGER[n] by modifying the first half-cleaner of BITONIC-SORTER[n]. The key is to perform the reversal of the the second half of the inputs implicitly. Given two sorted sequences
The resulting merging network is shown in Figure 28.11. Only the first stage of MERGER[n] is different from BITONIC-SORTER[n]. Consequently, the depth of MERGER[n] is lg n, the same as that of BITONIC-SORTER[n].
28.4-1
Prove an analog of the zero-one principle for merging networks. Specifically, show that a comparison network that can merge any two monotonically increasing sequences of 0's and 1's can merge any two monotonically increasing sequences of arbitrary numbers.
28.4-2
How many different zero-one input sequences must be applied to the input of a comparison network to verify that it is a merging network?
28.4-3
Show that any network that can merge 1 item with n - 1 items to produce a sorted sequence of length n must have depth at least lg n.
28.4-4
Consider a merging network with inputs a1, a2, . . . , an, for n an exact power of 2, in which the two monotonic sequences to be merged are
28.4-5
Prove that any merging network, regardless of the order of inputs, requires
We now have all the necessary tools to construct a network that can sort any input sequence. The sorting network SORTER[n] uses the merging network to implement a parallel version of merge sort from Section 1.3.1. The construction and operation of the sorting network are illustrated in Figure 28.12.
Figure 28.12(a) shows the recursive construction of SORTER[n]. The n input elements are sorted by using two copies of SORTER[n/2] recursively to sort (in parallel) two subsequences of length n/2 each. The two resulting sequences are then merged by MERGER[n]. The boundary case for the recursion is when n = 1, in which case we can use a wire to sort the 1-element sequence, since a 1-element sequence is already sorted. Figure 28.12(b) shows the result of unrolling the recursion, and Figure 28.12(c) shows the actual network obtained by replacing the MERGER boxes in Figure 28.12(b) with the actual merging networks.
Data pass through lg n stages in the network SORTER[n]. Each of the individual inputs to the network is already a sorted 1-element sequence. The first stage of SORTER[n] consists of n/2 copies of MERGER[2] that work in parallel to merge pairs of 1-element sequences to produce sorted sequences of length 2. The second stage consists of n/4 copies of MERGER[4] that merge pairs of these 2-element sorted sequences to produce sorted sequences of length 4. In general, for k = 1, 2, . . . , lg n, stage k consists of n/2k copies of MERGER[2k] that merge pairs of the 2k-1-element sorted sequences to produce sorted sequences of length 2k. At the final stage, one sorted sequence consisting of all the input values is produced. This sorting network can be shown by induction to sort zero-one sequences, and consequently, by the zero-one principle (Theorem 28.2), it can sort arbitrary values.
We can analyze the depth of the sorting network recursively. The depth D(n) of SORTER[n] is the depth D(n/2) of SORTER[n/2] (there are two copies of SORTER[n/2], but they operate in parallel) plus the depth lg n of MERGER[n]. Consequently, the depth of SORTER[n] is given by the recurrence
whose solution is D(n) =
28.5-1
How many comparators are there in SORTER[n]?
28.5-2
Show that the depth of SORTER[n] is exactly (lg n)(lgn + 1)/2.
28.5-3
Suppose we modify a comparator to take two sorted lists of length k as inputs, merge them, and output the largest k to its "max" output and the smallest k to its "min" output. Show that any sorting network on n inputs with comparators modified in this fashion can sort nk numbers, assuming that each input to the network is a sorted list of length k.
28.5-4
Suppose that we have 2n elements
28.5-5
Let S(k) be the depth of a sorting network with k inputs, and let M(k) be the depth of a merging network with 2k inputs. Suppose that we have a sequence of n numbers to be sorted and know that every number is within k positions of its correct position in the sorted order. Show that we can sort the n numbers in depth S(k) + 2M(k).
28.5-6
We can sort the elements of an m X m matrix by repeating the following procedure k times:
1. Sort each odd-numbered row into monotonically increasing order.
2. Sort each even-numbered row into monotonically decreasing order.
3. Sort each column into monotonically increasing order.
How many iterations k are required for this procedure to sort, and what is the pattern of the sorted output?
28-1 Transposition sorting networks
A comparison network is a transposition network if each comparator connects adjacent lines, as in the network in Figure 28.3.
a. Show that any transposition network with n inputs that sorts has
b. Prove that a transposition network with n inputs is a sorting network if and only if it sorts the sequence
An odd-even sorting network on n inputs
c. Prove that the family of odd-even sorting networks is indeed a family of sorting networks.
28-2 Batcher's odd-even merging network
In Section 28.4, we saw how to construct a merging network based on bitonic sorting. In this problem, we shall construct an odd-even merging network. We assume that n is an exact power of 2, and we wish to merge the sorted sequence of elements on lines
a. Draw a 2n-input merging network for n = 4.
b. Use the zero-one principle to prove that any 2n-input odd-even merging network is indeed a merging network.
c. What is the depth of a 2n-input odd-even merging network? What is its size?
28-3 Permutation networks
A permutation network on n inputs and n outputs has switches that allow it to connect its inputs to its outputs according to any of the n! possible permutations. Figure 28.14(a) shows the 2-input, 2-output permutation network P2, which consists of a single switch that can be set either to feed its inputs straight through to its outputs or to cross them.
a. Argue that if we replace each comparator in a sorting network with the switch of Figure 28.14(a), the resulting network is a permutation network. That is, for any permutation
Figure 28.14(b) shows the recursive construction of an 8-input, 8-output permutation network P8 that uses two copies of P4 and 8 switches. The switches have been set to realize the permutation
b. Show how to realize the permutation
Let n be an exact power of 2. Define Pn recursively in terms of two Pn/2's in a manner similar to the way we defined P8.
c. Describe an O(n)-time (ordinary random-access machine) algorithm that sets the n switches connected to the inputs and outputs of Pn and specifies the permutations that must be realized by each Pn/2 in order to accomplish any given n-element permutation. Prove that your algorithm is correct.
d. What are the depth and size of Pn? How long does it take on an ordinary random-access machine to compute all switch settings, including those within the Pn/2's?
e. Argue that for n > 2, any permutation network--not just Pn--must realize some permutation by two distinct combinations of switch settings.
Knuth [123] contains a discussion of sorting networks and charts their history. They apparently were first explored in 1954 by P. N. Armstrong, R. J. Nelson, and D. J. O'Connor. In the early 1960's, K. E. Batcher discovered the first network capable of merging two sequences of n numbers in O(lg n) time. He used odd-even merging (see Problem 28-2), and he also showed how this technique could be used to sort n numbers in O(lg2 n) time. Shortly afterwards, he discovered an O(lg n)-depth bitonic sorter similar to the one presented in Section 28.3. Knuth attributes the zero-one principle to W. G. Bouricius (1954), who proved it in the context of decision trees.
For a long time, the question remained open as to whether a sorting network with depth O(lg n) exists. In 1983, the answer was shown to be a somewhat unsatisfying yes. The AKS sorting network (named after its developers, Ajtai, Komlós, and Szemerédi [8]) can sort n numbers in depth O(lg n) using O(n lg n) comparators. Unfortunately, the constants hidden by the O-notation are quite large (many, many thousands), and thus it cannot be considered practical.

Figure 28.1 (a) A comparator with inputs x and y and outputs x' and y'. (b) The same comparator, drawn as a single vertical line. Inputs x = 7, y = 3 and outputs x' = 3, y' = 7 are shown.
x' = min(x, y) ,
y' = max(x, y) .
 a1, a2, . . . , an
a1, a2, . . . , an and the output sequence
and the output sequence  b1,b2, . . . ,bn
b1,b2, . . . ,bn , referring to the values on the input and output wires. That is, we use the same name for both a wire and the value it carries. Our intention will always be clear from the context.
, referring to the values on the input and output wires. That is, we use the same name for both a wire and the value it carries. Our intention will always be clear from the context.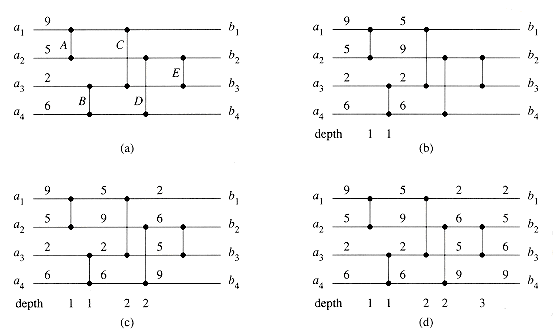
Figure 28.2 (a) A 4-input, 4-output comparison network, which is in fact a sorting network. At time 0, the input values shown appear on the four input wires. (b) At time 1, the values shown appear on the outputs of comparators A and B, which are at depth l. (c) At time 2, the values shown appear on the outputs of comparators C and D, at depth 2. Output wires b1 and b4 now have their final values, but output wires b2 and b3 do not. (d) At time 3, the values shown appear on the outputs of comparator E, at depth 3. Output wires b2 and b3 now have their final values.
 9, 5, 2, 6
9, 5, 2, 6 appears on the input wires at time 0. At time 0, then, only comparators A and B have all their input values available. Assuming that each comparator requires one time unit to compute its output values, comparators A and B produce their outputs at time 1; the resulting values are shown in Figure 28.2(b). Note that comparators A and B produce their values at the same time, or "in parallel." Now, at time 1, comparators C and D, but not E, have all their input values available. One time unit later, at time 2, they produce their outputs, as shown in Figure 28.2(c). Comparators C and D operate in parallel as well. The top output of comparator C and the bottom output of comparator D connect to output wires b1 and b4, respectively, of the comparison network, and these network output wires therefore carry their final values at time 2. Meanwhile, at time 2, comparator E has its inputs available, and Figure 28.2(d) shows that it produces its output values at time 3. These values are carried on network output wires b2 and b3, and the output sequence
appears on the input wires at time 0. At time 0, then, only comparators A and B have all their input values available. Assuming that each comparator requires one time unit to compute its output values, comparators A and B produce their outputs at time 1; the resulting values are shown in Figure 28.2(b). Note that comparators A and B produce their values at the same time, or "in parallel." Now, at time 1, comparators C and D, but not E, have all their input values available. One time unit later, at time 2, they produce their outputs, as shown in Figure 28.2(c). Comparators C and D operate in parallel as well. The top output of comparator C and the bottom output of comparator D connect to output wires b1 and b4, respectively, of the comparison network, and these network output wires therefore carry their final values at time 2. Meanwhile, at time 2, comparator E has its inputs available, and Figure 28.2(d) shows that it produces its output values at time 3. These values are carried on network output wires b2 and b3, and the output sequence  2, 5, 6, 9
2, 5, 6, 9 is now complete.
is now complete. b2
b2  . . .
. . .  bn) for every input sequence. Of course, not every comparison network is a sorting network, but the network of Figure 28.2 is. To see why, observe that after time 1, the minimum of the four input values has been produced by either the top output of comparator A or the top output of comparator B. After time 2, therefore, it must be on the top output of comparator C. A symmetrical argument shows that after time 2, the maximum of the four input values has been produced by the bottom output of comparator D. All that remains is for comparator E to ensure that the middle two values occupy their correct output positions, which happens at time 3.
bn) for every input sequence. Of course, not every comparison network is a sorting network, but the network of Figure 28.2 is. To see why, observe that after time 1, the minimum of the four input values has been produced by either the top output of comparator A or the top output of comparator B. After time 2, therefore, it must be on the top output of comparator C. A symmetrical argument shows that after time 2, the maximum of the four input values has been produced by the bottom output of comparator D. All that remains is for comparator E to ensure that the middle two values occupy their correct output positions, which happens at time 3.
Figure 28.3 A sorting network based on insertion sort for use in Exercise 28.1-6.
Exercises
 9, 6, 5, 2
9, 6, 5, 2 .
. (n lg n).
(n lg n).28.2 The zero-one principle
 a1, a2, . . . , an
a1, a2, . . . , an into the output sequence b =
into the output sequence b =  b1, b2, . . . , bn
b1, b2, . . . , bn , then for any monotonically increasing function f, the network transforms the input sequence f(a) =
, then for any monotonically increasing function f, the network transforms the input sequence f(a) =  f(a1), f(a2), . . . , f(an)
f(a1), f(a2), . . . , f(an) into the output sequence f(b) =
into the output sequence f(b) =  f(b1), f(b2), . . . , f(bn)
f(b1), f(b2), . . . , f(bn) .
. y implies f(x)
y implies f(x)  f(y). Consequently, we have the identities
f(y). Consequently, we have the identitiesmin(f(x), f(y)) = f(min(x,y)) ,
max(f(x), f(y)) = f(max(x,y)) .

Figure 28.4 The operation of the comparator in the proof of Lemma 28.1. The function f is monotonically increasing.
 1. The wire is the output of a comparator at depth d, and the input wires to this comparator are at a depth strictly less than d. By the inductive hypothesis, therefore, if the input wires to the comparator carry values ai and aj when the input sequence a is applied, then they carry f(ai) and f(aj) when the input sequence f(a) is applied. By our earlier claim, the output wires of this comparator then carry f(min(ai, aj)) and f(max(ai, aj)). Since they carry min(ai, aj) and max(ai, aj) when the input sequence is a, the lemma is proved.
1. The wire is the output of a comparator at depth d, and the input wires to this comparator are at a depth strictly less than d. By the inductive hypothesis, therefore, if the input wires to the comparator carry values ai and aj when the input sequence a is applied, then they carry f(ai) and f(aj) when the input sequence f(a) is applied. By our earlier claim, the output wires of this comparator then carry f(min(ai, aj)) and f(max(ai, aj)). Since they carry min(ai, aj) and max(ai, aj) when the input sequence is a, the lemma is proved.  x/2
x/2 applied to the inputs. The value on every wire is f applied to the value on the same wire in Figure 28.2.
applied to the inputs. The value on every wire is f applied to the value on the same wire in Figure 28.2.
Figure 28.5 (a) The sorting network from Figure 28.2 with input sequence
 9, 5, 2, 6
9, 5, 2, 6 . (b) The same sorting network with the monotonically increasing function f(x) = f(
. (b) The same sorting network with the monotonically increasing function f(x) = f( x/2
x/2 ) applied to the inputs. Each wire in this network has the value of f applied to the value on the corresponding wire in (a).
) applied to the inputs. Each wire in this network has the value of f applied to the value on the corresponding wire in (a). a1, a2, . . . , an
a1, a2, . . . , an containing elements ai and aj such that ai < aj, but the network places aj before ai in the output sequence. We define a monotonically increasing function f as
containing elements ai and aj such that ai < aj, but the network places aj before ai in the output sequence. We define a monotonically increasing function f as
 a1, a2, . . . , an
a1, a2, . . . , an is input, it follows from Lemma 28.1 that it places f(aj) before f(ai) in the output sequence when
is input, it follows from Lemma 28.1 that it places f(aj) before f(ai) in the output sequence when  f(a1), f(a2), . . . , f(an)
f(a1), f(a2), . . . , f(an) is input. But since f(aj) = 1 and f(ai) = 0, we obtain the contradiction that the network fails to sort the zero-one sequence
is input. But since f(aj) = 1 and f(ai) = 0, we obtain the contradiction that the network fails to sort the zero-one sequence  f(a1), f(a2), . . . , f(an)
f(a1), f(a2), . . . , f(an) correctly.
correctly. Exercises
 n, n - 1, . . . , 1
n, n - 1, . . . , 1 if and only if it correctly sorts the n - 1 zero-one sequences
if and only if it correctly sorts the n - 1 zero-one sequences  1, 0, 0, . . . , 0, 0
1, 0, 0, . . . , 0, 0 ,
,  1, 1, 0, . . . , 0, 0
1, 1, 0, . . . , 0, 0 , . . . ,
, . . . ,  1, 1, 1, . . . , 1, 0
1, 1, 1, . . . , 1, 0 .
.
Figure 28.6 A sorting network for sorting 4 numbers.
28.3 A bitonic sorting network
 1, 4, 6, 8, 3, 2
1, 4, 6, 8, 3, 2 and
and  9, 8, 3, 2, 4, 6
9, 8, 3, 2, 4, 6 are both bitonic. The zero-one sequences that are bitonic have a simple structure. They have the form 0i1j0k or the form 1i0j1k, for some i, j, k
are both bitonic. The zero-one sequences that are bitonic have a simple structure. They have the form 0i1j0k or the form 1i0j1k, for some i, j, k  0. Note that a sequence that is either monotonically increasing or monotonically decreasing is also bitonic.
0. Note that a sequence that is either monotonically increasing or monotonically decreasing is also bitonic.The half-cleaner

Figure 28.7 The comparison network HALF-CLEANER[8]. Two different sample zero-one input and output values are shown. The input is assumed to be bitonic. A half-cleaner ensures that every output element of the top half is at least as small as every output element of the bottom half. Moreover, both halves are bitonic, and at least one half is clean.
The bitonic sorter

Figure 28.8 The possible comparisons in HALF-CLEANER[n]. The input sequence is assumed to be a bitonic sequence of 0's and 1's, and without loss of generality, we assume that it is of the form 00 . . . 011 . . . 100 . . . 0. Subsequences of 0's are white, and subsequences of 1's are gray. We can think of the n inputs as being divided into two halves such that for i = 1, 2, . . . , n/2, inputs i and i + n/2 are compared. (a)-(b) Cases in which the division occurs in the middle subsequence of 1's. (c)-(d) Cases in which the division occurs in a subsequence of 0's. For all cases, every element in the top half is at least as small as every element in the bottom half, both halves are bitonic, and at least one half is clean.

Figure 28.9 The comparison network BITONIC-SORTER[n], shown here for n = 8. (a) The recursive construction: HALF-CLEANER[n] followed by two copies of BITONIC-SORTER[n/2] that operate in parallel. (b) The network after unrolling the recursion. Each half-cleaner is shaded. Sample zero-one values are shown on the wires.

Exercises
 (n lg n) comparators.
(n lg n) comparators.28.4 A merging network
 a1, a2, . . . , an/2
a1, a2, . . . , an/2 and
and  an/2+1, an/2+2, . . . , an
an/2+1, an/2+2, . . . , an to be merged, we want the effect of bitonically sorting the sequence
to be merged, we want the effect of bitonically sorting the sequence  a1, a2, . . . , an/2, an, an-1, . . . , an/2+1
a1, a2, . . . , an/2, an, an-1, . . . , an/2+1 . Since the half-cleaner of BITONIC-SORTER[n] compares inputs i and n/2 + i, for i = 1, 2, . . . , n/2, we make the first stage of the merging network compare inputs i and n - i + 1. Figure 28.10 shows the correspondence. The only subtlety is that the order of the outputs from the bottom of the first stage of MERGER[n] are reversed compared with the order of outputs from an ordinary half-cleaner. Since the reversal of a bitonic sequence is bitonic, however, the top and bottom outputs of the first stage of the merging network satisfy the properties in Lemma 28.3, and thus the top and bottom can be bitonically sorted in parallel to produce the sorted output of the merging network.
. Since the half-cleaner of BITONIC-SORTER[n] compares inputs i and n/2 + i, for i = 1, 2, . . . , n/2, we make the first stage of the merging network compare inputs i and n - i + 1. Figure 28.10 shows the correspondence. The only subtlety is that the order of the outputs from the bottom of the first stage of MERGER[n] are reversed compared with the order of outputs from an ordinary half-cleaner. Since the reversal of a bitonic sequence is bitonic, however, the top and bottom outputs of the first stage of the merging network satisfy the properties in Lemma 28.3, and thus the top and bottom can be bitonically sorted in parallel to produce the sorted output of the merging network.
Figure 28.10 Comparing the first stage of MERGER[n] with HALF-CLEANER[n], for n = 8. (a) The first stage of MERGER[n] transforms the two monotonic input sequences
 a1, a2, . . . , an/2
a1, a2, . . . , an/2 and
and  an/2+1, an/2+2, . . . , an
an/2+1, an/2+2, . . . , an into two bitonic sequences
into two bitonic sequences  b1, b2, . . . , bn/2
b1, b2, . . . , bn/2 and
and  bn/2+1, bn/2+2, . . . , bn
bn/2+1, bn/2+2, . . . , bn . (b) The equivalent operation for HALF-CLEANER[n]. The bitonic input sequence
. (b) The equivalent operation for HALF-CLEANER[n]. The bitonic input sequence  a1, a2, . . . , an/2-1, an/2, an, an-1, . . . , an/2+2, an/2+1
a1, a2, . . . , an/2-1, an/2, an, an-1, . . . , an/2+2, an/2+1 is transformed into the two bitonic sequences
is transformed into the two bitonic sequences  b1, b2, . . . , bn/2
b1, b2, . . . , bn/2 and
and  bn, bn-1, . . . , bn/2+1
bn, bn-1, . . . , bn/2+1 .
.
Figure 28.11 A network that merges two sorted input sequences into one sorted output sequence. The network MERGER[n] can be viewed as BITONIC-SORTER[n] with the first half-cleaner altered to compare inputs i and n - i + 1 for i = 1, 2, . . . , n/2. Here, n = 8. (a) The network decomposed into the first stage followed by two parallel copies of BITONIC-SORTER[n/2]. (b) The same network with the recursion unrolled. Sample zero-one values are shown on the wires, and the stages are shaded.
Exercises
 a1, a3, . . . , an-1
a1, a3, . . . , an-1 and
and  a2, a4, . . . , an
a2, a4, . . . , an . Prove that the number of comparators in this kind of merging network is
. Prove that the number of comparators in this kind of merging network is  (n lg n). Why is this an interesting lower bound? (Hint: Partition the comparators into three sets.)
(n lg n). Why is this an interesting lower bound? (Hint: Partition the comparators into three sets.) (n lg n) comparators.
(n lg n) comparators.28.5 A sorting network

Figure 28.12 The sorting network SORTER[n] constructed by recursively combining merging networks. (a) The recursive construction. (b) Unrolling the recursion. (c) Replacing the MERGER boxes with the actual merging networks. The depth of each comparator is indicated, and sample zero-one values are shown on the wires.

 (lg2 n). Thus, we can sort n numbers in parallel in O(lg2 n) time.
(lg2 n). Thus, we can sort n numbers in parallel in O(lg2 n) time.Exercises
 a1, a2, . . . , a2n
a1, a2, . . . , a2n and wish to partition them into the n smallest and the n largest. Prove that we can do this in constant additional depth after separately sorting
and wish to partition them into the n smallest and the n largest. Prove that we can do this in constant additional depth after separately sorting  a1,a2, . . . , an
a1,a2, . . . , an and
and  an+1, an+2, . . . , a2n
an+1, an+2, . . . , a2n .
.Problems
 (n2) comparators.
(n2) comparators. n, n- 1, . . . , 1
n, n- 1, . . . , 1 . (Hint: Use an induction argument analogous to the one in the proof of Lemma 28.1.)
. (Hint: Use an induction argument analogous to the one in the proof of Lemma 28.1.) a1, a2, . . . , an
a1, a2, . . . , an has n levels of comparators. Figure 28.13 shows an odd-even transposition network on 8 inputs. As can be seen in the figure, for i = 2, 3, . . . , n - 1 and d = 1, 2, . . . , n, line i is connected by a depth-d comparator to line j = i + (-1)i+d if 1
has n levels of comparators. Figure 28.13 shows an odd-even transposition network on 8 inputs. As can be seen in the figure, for i = 2, 3, . . . , n - 1 and d = 1, 2, . . . , n, line i is connected by a depth-d comparator to line j = i + (-1)i+d if 1  j
j  n.
n. a1, a2, . . . , an
a1, a2, . . . , an with those on lines
with those on lines  an+1, an+2, . . . , a2n
an+1, an+2, . . . , a2n . We recursively construct two odd-even merging networks that merge sorted subsequences in parallel. The first merges the sequence on lines
. We recursively construct two odd-even merging networks that merge sorted subsequences in parallel. The first merges the sequence on lines  a1, a3, . . . , an-1
a1, a3, . . . , an-1 with the sequence on lines
with the sequence on lines  an+1, an+3, . . . , a2n-1
an+1, an+3, . . . , a2n-1 (the odd elements). The second merges
(the odd elements). The second merges  a2, a4, . . . , an
a2, a4, . . . , an with
with  an+2, an+4, . . . , a2n
an+2, an+4, . . . , a2n (the even elements). To combine the two sorted subsequences, we put a comparator between a2i-1 and a2i for i = 1, 2, . . . , n.
(the even elements). To combine the two sorted subsequences, we put a comparator between a2i-1 and a2i for i = 1, 2, . . . , n.
Figure 28.13 An odd-even sorting network on 8 inputs.

Figure 28.14 Permutation networks. (a) The permutation network P2, which consists of a single switch that can be set in either of the two ways shown. (b) The recursive construction of P8 from 8 switches and two P4's. The switches and P4's are set to realize the permutation
 =
=  4, 7, 3, 5, 1, 6, 8, 2
4, 7, 3, 5, 1, 6, 8, 2 .
. , there is a way to set the switches in the network so that input i is connected to output
, there is a way to set the switches in the network so that input i is connected to output  (i).
(i). =
=  4, 7, 3, 5, 1, 6, 8, 2
4, 7, 3, 5, 1, 6, 8, 2 , which requires (recursively) that the top P4 realize
, which requires (recursively) that the top P4 realize  4, 2, 3, 1
4, 2, 3, 1 and the bottom P4 realize
and the bottom P4 realize  2, 3, 1, 4
2, 3, 1, 4 .
. 5, 3, 4, 6, 1, 8, 2, 7
5, 3, 4, 6, 1, 8, 2, 7 on P8 by drawing the switch settings and the permutations performed by the two P4's.
on P8 by drawing the switch settings and the permutations performed by the two P4's.Chapter notes


