The subject of this chapter, however, is an interesting class of problems, called the "NP-complete" problems, whose status is unknown. No polynomial-time algorithm has yet been discovered for an NP-complete problem, nor has anyone yet been able to prove a superpolynomial-time lower bound for any of them. This so-called P  NP question has been one of the deepest, most perplexing open research problems in theoretical computer science since it was posed in 1971.
NP question has been one of the deepest, most perplexing open research problems in theoretical computer science since it was posed in 1971.
Most theoretical computer scientists believe that the NP-complete problems are intractable. The reason is that if any single NP-complete problem can be solved in polynomial time, then every NP-complete problem has a polynomial-time algorithm. Given the wide range of NP-complete problems that have been studied to date, without any progress toward a polynomial-time solution, it would be truly astounding if all of them could be solved in polynomial time.
To become a good algorithm designer, you must understand the rudiments of the theory of NP-completeness. If you can establish a problem as NP-complete, you provide good evidence for its intractability. As an engineer, you would then do better spending your time developing an approximation algorithm (see Chapter 37) rather than searching for a fast algorithm that solves the problem exactly. Moreover, many natural and interesting problems that on the surface seem no harder than sorting, graph searching, or network flow are in fact NP-complete. Thus, it is important to become familiar with this remarkable class of problems.
This chapter studies the aspects of NP-completeness that bear most directly on the analysis of algorithms. In Section 36.1, we formalize our notion of "problem" and define the complexity class P of polynomial-time solvable decision problems. We also see how these notions fit into the framework of formal-language theory. Section 36.2 defines the class NP of decision problems whose solutions can be verified in polynomial time. It also formally poses the P  NP question.
NP question.
Section 36.3 shows how relationships between problems can be studied via polynomial-time "reductions." It defines NP-completeness and sketches a proof that one problem, called "circuit satisfiability," is NP-complete. Having found one NP-complete problem, we show in Section 36.4 how other problems can be proven to be NP-complete much more simply by the methodology of reductions. The methodology is illustrated by showing that two formula-satisfiability problems are NP-complete. A variety of other problems are shown to be NP-complete in Section 36.5.
36.1 Polynomial time
We begin our study of NP-completeness by formalizing our notion of polynomial-time solvable problems. These problems are generally regarded as tractable. The reason why is a philosophical, not a mathematical, issue. We can offer three supporting arguments.
First, although it is reasonable to regard a problem that requires time  (n100) as intractable, there are very few practical problems that require time on the order of such a high-degree polynomial. The polynomial-time computable problems encountered in practice typically require much less time.
(n100) as intractable, there are very few practical problems that require time on the order of such a high-degree polynomial. The polynomial-time computable problems encountered in practice typically require much less time.
Second, for many reasonable models of computation, a problem that can be solved in polynomial time in one model can be solved in polynomial time in another. For example, the class of problems solvable in polynomial time by the serial random-access machine used throughout most of this book is the same as the class of problems solvable in polynomial time on abstract Turing machines.1 It is also the same as the class of problems solvable in polynomial time on a parallel computer, even if the number of processors grows polynomially with the input size.
1See Hopcroft and Ullman [104] or Lewis and Papadimitriou [139] for a thorough treatment of the Turing-machine model. of calls to polynomial-time subroutines, the running time of the composite algorithm is polynomial.
Third, the class of polynomial-time solvable problems has nice closure properties, since polynomials are closed under addition, multiplication, and composition. For example, if the output of one polynomial-time algorithm is fed into the input of another, the composite algorithm is polynomial. If an otherwise polynomial-time algorithm makes a constant number of calls to polynomial-time subroutines, the running time of the composite algorithm is polynomial.
Abstract problems
To understand the class of polynomial-time solvable problems, we must first have a formal notion of what a "problem" is. We define an abstract problem Q to be a binary relation on a set I of problem instances and a set S of problem solutions. For example, consider the problem SHORTEST-PATH of finding a shortest path between two given vertices in an unweighted, undirected graph G = (V, E). An instance for SHORTEST-PATH is a triple consisting of a graph and two vertices. A solution is a sequence of vertices in the graph, with perhaps the empty sequence denoting that no path exists. The problem SHORTEST-PATH itself is the relation that associates each instance of a graph and two vertices with a shortest path in the graph that connects the two vertices. Since shortest paths are not necessarily unique, a given problem instance may have more than one solution.
This formulation of an abstract problem is more general than is required for our purposes. For simplicity, the theory of NP-completeness restricts attention to decision problems: those having a yes/no solution. In this case, we can view an abstract decision problem as a function that maps the instance set I to the solution set {0, 1}. For example, a decision problem PATH related to the shortest-path problem is, "Given a graph G = (V, E), two vertices u, v
Many abstract problems are not decision problems, but rather optimization problems, in which some value must be minimized or maximized. In order to apply the theory of NP-completeness to optimization problems, we must recast them as decision problems. Typically, an optimization problem can be recast by imposing a bound on the value to be optimized. As an example, in recasting the shortest-path problem as the decision problem PATH, we added a bound k to the problem instance.
Although the theory of NP-completeness compels us to recast optimization problems as decision problems, this requirement does not diminish the impact of the theory. In general, if we can solve an optimization problem quickly, we can also solve its related decision problem quickly. We simply compare the value obtained from the solution of the optimization problem with the bound provided as input to the decision problem. If an optimization problem is easy, therefore, its related decision problem is easy as well. Stated in a way that has more relevance to NP-completeness, if we can provide evidence that a decision problem is hard, we also provide evidence that its related optimization problem is hard. Thus, even though it restricts attention to decision problems, the theory of NP-completeness applies much more widely.
If a computer program is to solve an abstract problem, problem instances must must be represented in a way that the program understands. An encoding of a set S of abstract objects is a mapping e from S to the set of binary strings.2 For example, we are all familiar with encoding the natural numbers N = {0, 1, 2, 3, 4, . . .} as the strings {0, 1, 10, 11, 100, . . .}. Using this encoding, e(l7) = 10001. Anyone who has looked at computer representations of keyboard characters is familiar with either the ASCII or EBCDIC codes. In the ASCII code, e(A) = 1000001. Even a compound object can be encoded as a binary string by combining the representations of its constituent parts. Polygons, graphs, functions, ordered pairs, programs--all can be encoded as binary strings.
2 The codomain of e need not be binary strings; any set of strings over a finite alphabet having at least 2 symbols will do.
Thus, a computer algorithm that "solves" some abstract decision problem actually takes an encoding of a problem instance as input. We call a problem whose instance set is the set of binary strings a concrete problem. We say that an algorithm solves a concrete problem in time O(T(n)) if, when it is provided a problem instance i of length n = |i|, the algorithm can produce the solution in at most O(T(n)) time. A concrete problem is polynomial-time solvable, therefore, if there exists an algorithm to solve it in time O(nk) for some constant k.
We can now formally define the complexity class P as the set of concrete decision problems that are solvable in polynomial time.
We can use encodings to map abstract problems to concrete problems. Given an abstract decision problem Q mapping an instance set I to {0, 1}, an encoding e : I
We would like to extend the definition of polynomial-time solvability from concrete problems to abstract problems using encodings as the bridge, but we would like the definition to be independent of any particular encoding. That is, the efficiency of solving a problem should not depend on how the problem is encoded. Unfortunately, it depends quite heavily. For example, suppose that an integer k is to be provided as the sole input to an algorithm, and suppose that the running time of the algorithm is
The encoding of an abstract problem is therefore quite important to our understanding of polynomial time. We cannot really talk about solving an abstract problem without first specifying an encoding. Nevertheless, in practice, if we rule out "expensive" encodings such as unary ones, the actual encoding of a problem makes little difference to whether the problem can be solved in polynomial time. For example, representing integers in base 3 instead of binary has no effect on whether a problem is solvable in polynomial time, since an integer represented in base 3 can be converted to an integer represented in base 2 in polynomial time.
We say that a function f : {0, 1}*
Lemma 36.1
Let Q be an abstract decision problem on an instance set I, and let e1 and e2 be polynomially related encodings on I. Then, e1(Q)
Proof We need only prove the forward direction, since the backward direction is symmetric. Suppose, therefore, that e1(Q) can be solved in time O(nk) for some constant k. Further, suppose that for any problem instance i, the encoding e1(i) can be computed from the encoding e2(i) in time O(nc) for some constant c, where n = |e1(i)|. To solve problem e2(Q), on input e2(i), we first compute e1(i) and then run the algorithm for e1(Q) on e1(i). How long does this take? The conversion of encodings takes time O(nc), and therefore |e1(i)| = O(nc), since the output of a serial computer cannot be longer than its running time. Solving the problem on e1 (i) takes time O(|e1(i)|k) = O(nck), which is polynomial since both c and k are constants.
Thus, whether an abstract problem has its instances encoded in binary or base 3 does not affect its "complexity," that is, whether it is polynomial-time solvable or not, but if instances are encoded in unary, its complexity may change. In order to be able to converse in an encoding-independent fashion, we shall generally assume that problem instances are encoded in any reasonable, concise fashion, unless we specifically say otherwise. To be precise, we shall assume that the encoding of an integer is polynomially related to its binary representation, and that the encoding of a finite set is polynomially related to its encoding as a list of its elements, enclosed in braces and separated by commas. (ASCII is one such encoding scheme.) With such a "standard" encoding in hand, we can derive reasonable encodings of other mathematical objects, such as tuples, graphs, and formulas. To denote the standard encoding of an object, we shall enclose the object in angle braces. Thus,
As long as we implicitly use an encoding that is polynomially related to this standard encoding, we can talk directly about abstract problems without reference to any particular encoding, knowing that the choice of encoding has no effect on whether the abstract problem is polynomial-time solvable. Henceforth, we shall generally assume that all problem instances are binary strings encoded using the standard encoding, unless we explicitly specify the contrary. We shall also typically neglect the distinction between abstract and concrete problems. The reader should watch out for problems that arise in practice, however, in which a standard encoding is not obvious and the encoding does make a difference.
One of the convenient aspects of focusing on decision problems is that they make it easy to use the machinery of formal-language theory. It is worthwhile at this point to review some definitions from that theory. An alphabet
There are a variety of operations on languages. Set-theoretic operations, such as union and intersection, follow directly from the set-theoretic definitions. We define the complement of L by
The closure or Kleene star of a language L is the language
where Lk is the language obtained by concatenating L to itself k times.
From the point of view of language theory, the set of instances for any decision problem Q is simply the set
For example, the decision problem PATH has the corresponding language
(Where convenient, we shall sometimes use the same name--PATH in this case--to refer to both a decision problem and its corresponding language.)
The formal-language framework allows us to express the relation between decision problems and algorithms that solve them concisely. We say that an algorithm A accepts a string x
Even if language L is accepted by an algorithm A, the algorithm will not necessarily reject a string x
As an example, the language PATH can be accepted in polynomial time. One polynomial-time accepting algorithm computes the shortest path from u to v in G, using breadth-first search, and then compares the distance obtained with k. If the distance is at most k, the algorithm outputs 1 and halts. Otherwise, the algorithm runs forever. This algorithm does not decide PATH, however, since it does not explicitly output 0 for instances in which the shortest path has length greater than k. A decision algorithm for PATH must explicitly reject binary strings that do not belong to PATH. For a decision problem such as PATH, such a decision algorithm is easy to design. For other problems, such as Turing's Halting Problem, there exists an accepting algorithm, but no decision algorithm exists.
We can informally define a complexity class as a set of languages, membership in which is determined by a complexity measure, such as running time, on an algorithm that determines whether a given string x belongs to language L. The actual definition of a complexity class is somewhat more technical--the interested reader is referred to the seminal paper by Hartmanis and Stearns [95].
Using this language-theoretic framework, wee can provide an alternative definition of the complexity class P:
In fact, P is also the class of languages that can be accepted in polynomial time.
Theorem 36.2
P = {L : L is accepted by a polynomial-time algorithm} .
Proof Since the class of languages decided by polynomial-time algorithms is a subset of the class of languages accepted by polynomial-time algorithms, we need only show that if L is accepted by a polynomial-time algorithm, it is decided by a polynomial-time algorithm. Let L be the language accepted by some polynomial-time algorithm A. We shall use a classic "simulation" argument to construct another polynomial-time algorithm A' that decides L. Because A accepts L in time O(nk) for some constant k, there also exists a constant c such that A accepts L in at most T = cnk steps. For any input string x, the algorithm A' simulates the action of A for time T. At the end of time T, algorithm A' inspects the behavior of A. If A has accepted x, then A' accepts x by outputting a 1. If A has not accepted x, then A' rejects x by outputting a 0. The overhead of A' simulating A does not increase the running time by more than a polynomial factor, and thus A' is a polynomial-time algorithm that decides L.
Note that the proof of Theorem 36.2 is nonconstructive. For a given language L
36.1-1
Define the optimization problem LONGEST-PATH-LENGTH as the relation that associates each instance of a undirected graph and two vertices with the length of the longest simple path between the two vertices. Define the decision problem LONGEST-PATH = {
36.1-2
Give a formal definition for the problem of finding the longest simple cycle in an undirected graph. Give a related decision problem. Give the language corresponding to the decision problem.
36.1-3
Give a formal encoding of directed graphs as binary strings using an adjacency-matrix representation. Do the same using an adjacency-list representation. Argue that the two representations are polynomially related.
36.1-4
Is the dynamic-programming algorithm for the 0-1 knapsack problem that is asked for in Exercise 17.2-2 a polynomial-time algorithm? Explain your answer.
36.1-5
Suppose that a language L can accept any string x
36.1-6
Show that an algorithm that makes at most a constant number of calls to polynomial-time subroutines runs in polynomial time, but that a polynomial number of calls to polynomial-time subroutines may result in an exponential-time algorithm.
36.1-7
Show that the class P, viewed as a set of languages, is closed under union, intersection, concatenation, complement, and Kleene star. That is, if Ll, L2
We now look at algorithms that "verify" membership in languages. For example, suppose that for a given instance
The problem of finding a hamiltonian cycle in an undirected graph has been studied for over a hundred years. Formally, a hamiltonian cycle of an undirected graph G = (V, E) is a simple cycle that contains each vertex in V. A graph that contains a hamiltonian cycle is said to be hamiltonian; otherwise, it is nonhamiltonian. Bondy and Murty [31] cite a letter by W. R. Hamilton describing a mathematical game on the dodecahedron (Figure 36.1(a)) in which one player sticks five pins in any five consecutive vertices and the other player must complete the path to form a cycle containing all the vertices. The dodecahedron is hamiltonian, and Figure 36.1 (a) shows one hamiltonian cycle. Not all graphs are hamiltonian, however. For example, Figure 36.1 (b) shows a bipartite graph with an odd number of vertices. (Exercise 36.2-2 asks you to show that all such graphs are nonhamiltonian.)
We can define the hamiltonian-cycle problem, "Does a graph G have a hamiltonian cycle?" as a formal language:
How might an algorithm decide the language HAM-CYCLE? Given a problem instance
Consider a slightly easier problem, however. Suppose that a friend tells you that a given graph G is hamiltonian, and then offers to prove it by giving you the vertices in order along the hamiltonian cycle. It would certainly be easy enough to verify the proof: simply verify that the provided cycle is hamiltonian by checking whether it is a permutation of the vertices of V and whether each of the consecutive edges along the cycle actually exists in the graph. This verification algorithm can certainly be implemented to run in O(n2) time, where n is the length of the encoding of G . Thus, a proof that a hamiltonian cycle exists in a graph can be verified in polynomial time.
We define a verification algorithm as being a two-argument algorithm A, where one argument is an ordinary input string x and the other is a binary string y called a certificate. A two-argument algorithm A verifies an input string x if there exists a certificate y such that A(x, y) = 1. The language verified by a verification algorithm A is
Intuitively, an algorithm A verifies a language L if for any string x
The complexity class NP is the class of languages that can be verified by a polynomial-time algorithm.3 More precisely, a language L belongs to NP if and only if there exists a two-input polynomial-time algorithm A and constant c such that
We say that algorithm A verifies language L in polynomial time.
3The name "NP" stands for "nondeterministic polynomial time." The class NP was originally studied in the context of nondeterminism, but this book uses the somewhat simpler yet equivalent notion of verification. Hopcroft and Ullman [104] give a good presentation of NP-completeness in terms of nondeterministic models of computation.
From our earlier discussion on the hamiltonian-cycle problem, it follows that HAM-CYCLE
It is unknown whether P = NP, but most researchers believe that P and NP are not the same class. Intuitively, the class P consists of problems that can be solved quickly. The class NP consists of problems for which a solution can be verified quickly. You may have learned from experience that it is often more difficult to solve a problem from scratch than to verify a clearly presented solution, especially when working under time constraints. Theoretical computer scientists generally believe that this analogy extends to the classes P and NP, and thus that NP includes languages that are not in P.
There is more compelling evidence that P
Many other fundamental questions beyond the P
Thus, our understanding of the precise relationship between P and NP is woefully incomplete. Nevertheless, by exploring the theory of NP-completeness, we shall find that our disadvantage in proving problems to be intractable is, from a practical point of view, not nearly so great as we might suppose.
36.2-1
Consider the language GRAPH-ISOMORPHISM = {
36.2-2
Prove that if G is an undirected bipartite graph with an odd number of vertices, then G is nonhamiltonian.
36.2-3
Show that if HAM-CYCLE
36.2-4
Prove that the class NP of languages is closed under union, intersection, concatenation, and Kleene star. Discuss the closure of NP under complement.
36.2-5
Show that any language in NP can be decided by an algorithm running in time 2O(nk) for some constant k.
36.2-6
A hamiltonian path in a graph is a simple path that visits every vertex exactly once. Show that the language HAM-PATH = {
36.2-7
Show that the hamiltonian-path problem can be solved in polynomial time on directed acyclic graphs. Give an efficient algorithm for the problem.
36.2-8
Let
36.2-9
Prove that P
36.2-10
Prove that if NP
36.2-11
Let G be a connected, undirected graph with at least 3 vertices, and let G3 be the graph obtained by connecting all pairs of vertices that are connected by a path in G of length at most 3. Prove that G3 is hamiltonian. (Hint: Construct a spanning tree for G, and use an inductive argument.)
Perhaps the most compelling reason why theoretical computer scientists believe that P
The language HAM-CYCLE is one NP-complete problem. If we could decide HAM-CYCLE in polynomial time, then we could solve every problem in NP in polynomial time. In fact, if NP - P should turn out to be nonempty, we could say with certainty that HAM-CYCLE
The NP-complete languages are, in a sense, the "hardest" languages in NP. In this section, we shall show how to compare the relative "hardness" of languages using a precise notion called "polynomial-time reducibility." First, we formally define the NP-complete languages, and then we sketch a proof that one such language, called CIRCUIT-SAT, is NP-complete. In Section 36.5, shall use the notion of reducibility to show that many other problems are NP-complete.
Intuitively, a problem Q can be reduced to another problem Q' if any instance of Q can be "easily rephrased" as an instance of Q', the solution to which provides a solution to the instance of Q. For example, the problem of solving linear equations in an indeterminate x reduces to the problem of solving quadratic equations. Given an instance ax + b = 0, we transform it to 0x2 + ax + b = 0, whose solution provides a solution to ax + b = 0. Thus, if a problem Q reduces to another problem Q', then Q is, in a sense, "no harder to solve" than Q'.
Returning to our formal-language framework for decision problems, we say that a language L1 is polynomial-time reducible to a language L2, written L1
We call the function f the reduction function, and a polynomial-time algorithm F that computes f is called a reduction algorithm.
Figure 36.3 illustrates the idea of a polynomial-time reduction from a language L1 to another language L2. Each language is a subset of {0, 1}*. The reduction function f provides a polynomial-time mapping such that if x
Polynomial-time reductions give us a powerful tool for proving that various languages belong to P.
Lemma 36.3
If L1, L2
Proof Let A2 be a polynomial-time algorithm that decides L2, and let F be a polynomial-time reduction algorithm that computes the reduction function f. We shall construct a polynomial-time algorithm A1 that decides L1.
Figure 36.4 illustrates the construction of A1. For a given input x
The correctness of A1 follows from condition (36.1). The algorithm runs in polynomial time, since both F and A2 run in polynomial time (see Exercise 36.1-6).
Polynomial-time reductions provide a formal means for showing that one problem is at least as hard as another, to within a polynomial-time factor. That is, if L1
A language L
1. L
2. L'
If a language L satisfies property 2, but not necessarily property 1, we say that L is NP-hard. We also define NPC to be the class of NP-complete languages.
As the following theorem shows, NP-completeness is at the crux of deciding whether P is in fact equal to NP.
Theorem 36.4
If any NP-complete problem is polynomial-time solvable, then P = NP. If any problem in NP is not polynomial-time solvable, then all NP-complete problems are not polynomial-time solvable.
Proof Suppose that L
To prove the second statement, suppose that there exists an L
It is for this reason that research into the P
We have defined the notion of an NP-complete problem, but up to this point, we have not actually proved that any problem is NP-complete. Once we prove that at least one problem is NP-complete, we can use polynomial-time reducibility as a tool to prove the NP-completeness of other problems. Thus, we now focus on demonstrating the existence of an NP-complete problem: the circuit-satisfiability problem.
Unfortunately, the formal proof that the circuit-satisfiability problem is NP-complete requires technical detail beyond the scope of this text. Instead, we shall informally describe a proof that relies on a basic understanding of boolean combinational circuits. This material is reviewed at the beginning of Chapter 29.
Figure 36.6 shows two boolean combinational circuits, each with three inputs and a single output. A truth assignment for a boolean combinational circuit is a set of boolean input values. We say that a one-output boolean combinational circuit is satisfiable if it has a satisfying assignment: a truth assignment that causes the output of the circuit to be 1. For example, the circuit in Figure 36.6(a) has the satisfying assignment
The circuit-satisfiability problem is, "Given a boolean combinational circuit composed of AND, OR, and NOT gates, is it satisfiable?" In order to pose this question formally, however, we must agree on a standard encoding for circuits. One can devise a graphlike encoding that maps any given circuit C into a binary string
The circuit-satisfiability problem has great importance in the area of computer-aided hardware optimization. If a circuit always produces 0, it can be replaced by a simpler circuit that omits all logic gates and provides the constant 0 value as its output. A polynomial-time algorithm for the problem would have considerable practical application.
Given a circuit C, we might attempt to determine whether it is satisfiable by simply checking all possible assignments to the inputs. Unfortunately, if there are k inputs, there are 2k possible assignments. When the size of C is polynomial in k, checking each one leads to a superpolynomial-time algorithm. In fact, as has been claimed, there is strong evidence that no polynomial-time algorithm exists that solves the circuit-satisfiability problem because circuit satisfiability is NP-complete. We break the proof of this fact into two parts, based on the two parts of the definition of NP-completeness.
Lemma 36.5
The circuit-satisfiability problem belongs to the class NP.
Proof We shall provide a two-input, polynomial-time algorithm A that can verify CIRCUIT-SAT. One of the inputs to A is (a standard encoding of) a boolean combinational circuit C. The other input is a certificate corresponding to an assignment of boolean values to the wires in C.
The algorithm A is constructed as follows. For each logic gate in the circuit, it checks that the value provided by the certificate on the output wire is correctly computed as a function of the values on the input wires. Then, if the output of the entire circuit is 1, the algorithm outputs 1, since the values assigned to the inputs of C provide a satisfying assignment. Otherwise, A outputs 0.
Whenever a satisfiable circuit C is input to algorithm A, there is a certificate whose length is polynomial in the size of C and that causes A to output a 1. Whenever an unsatisfiable circuit is input, no certificate can fool A into believing that the circuit is satisfiable. Algorithm A runs in polynomial time: with a good implementation, linear time suffices. Thus, CIRCUIT-SAT can be verified in polynomial time, and CIRCUIT-SAT
The second part of proving that CIRCUIT-SAT is NP-complete is to show that the language is NP-hard. That is, we must show that every language in NP is polynomial-time reducible to CIRCUIT-SAT. The actual proof of this fact is full of technical intricacies, and so we shall settle for a sketch of the proof based on some understanding of the workings of computer hardware.
A computer program is stored in the computer memory as a sequence of instructions. A typical instruction encodes an operation to be performed, addresses of operands in memory, and an address where the result is to be stored. A special memory location, called the program counter, keeps track of which instruction is to be executed next. The program counter is automatically incremented whenever an instruction is fetched, thereby causing the computer to execute instructions sequentially. The execution of an instruction can cause a value to be written to the program counter, however, and then the normal sequential execution can be altered, allowing the computer to loop and perform conditional branches.
At any point during the execution of a program, the entire state of the computation is represented in the computer's memory. (We take the memory to include the program itself, the program counter, working storage, and any of the various bits of state that a computer maintains for bookkeeping.) We call any particular state of computer memory a configuration. The execution of an instruction can be viewed as mapping one configuration to another. Importantly, the computer hardware that accomplishes this mapping can be implemented as a boolean combinational circuit, which we denote by M in the proof of the following lemma.
Lemma 36.6
The circuit-satisfiability problem is NP-hard.
Proof Let L be any language in NP. We shall describe a polynomial-time algorithm F computing a reduction function â that maps every binary string x to a circuit C = â(x) such that x
Since L
Let T(n) denote the worst-case running time of algorithm A on length-n input strings, and let k
The basic idea of the proof is to represent the computation of A as a sequence of configurations. As shown in Figure 36.7, each configuration can be broken into parts consisting of the program for A, the program counter and auxiliary machine state, the input x, the certificate y, and working storage. Starting with an initial configuration c0, each configuration ci is mapped to a subsequent configuration ci+1 by the combinational circuit M implementing the computer hardware. The output of the algorithm A--0 or 1--is written to some designated location in the working storage when A finishes executing, and if we assume that thereafter A halts, the value never changes. Thus, if the algorithm runs for at most T(n) steps, the output appears as one of the bits in cT(n).
The reduction algorithm F constructs a single combinational circuit that computes all configurations produced by a given initial configuration. The idea is to paste together T(n) copies of the circuit M. The output of the ith circuit, which produces configuration ci, is fed directly into the input of the (i + 1)st circuit. Thus, the configurations, rather than ending up in a state register, simply reside as values on the wires connecting copies of M.
Recall what the polynomial-time reduction algorithm F must do. Given an input x, it must compute a circuit C = â(x) that is satisfiable if and only if there exists a certificate y such that A(x, y) = 1. When F obtains an input x, it first computes n = |x| and constructs a combinational circuit C' consisting of T(n) copies of M. The input to C' is an initial configuration corresponding to a computation on A(x, y), and the output is the configuration cT(n).
The circuit C = â(x) that F computes is obtained by modifying C' slightly. First, the inputs to C' corresponding to the program for A, the initial program counter, the input x, and the initial state of memory are wired directly to these known values. Thus, the only remaining inputs to the circuit correspond to the certificate y. Second, all outputs to the circuit are ignored, except the one bit of cT(n) corresponding to the output of A. This circuit C, so constructed, computes C(y) = A(x, y) for any input y of length O(nk). The reduction algorithm F, when provided an input string x, computes such a circuit C and outputs it.
Two properties remain to be proved. First, we must show that F correctly computes a reduction function â. That is, we must show that C is satisfiable if and only if there exists a certificate y such that A(x, y) = 1. Second, we must show that F runs in polynomial time.
To show that F correctly computes a reduction function, let us suppose that there exists a certificate y of length O(nk) such that A(x, y) = 1. Then, if we apply the bits of y to the inputs of C, the output of C is C(y) = A(x, y) = 1. Thus, if a certificate exists, then C is satisfiable. For the other direction, suppose that C is satisfiable. Hence, there exists an input y to C such that C(y) = 1, from which we conclude that A(x, y) = 1. Thus, F correctly computes a reduction function.
To complete the proof, we need only show that F runs in time polynomial in n = |x|. The first observation we make is that the number of bits required to represent a configuration is polynomial in n. The program for A itself has constant size, independent of the length of its input x. The length of the input x is n, and the length of the certificate y is O(nk). Since the algorithm runs for at most O(nk) steps, the amount of working storage required by A is polynomial in n as well. (We assume that this memory is contiguous; Exercise 36.3-4 asks you to extend the argument to the situation in which the locations accessed by A are scattered across a much larger region of memory and the particular pattern of scattering can differ for each input x.)
The combinational circuit M implementing the computer hardware has size polynomial in the length of a configuration, which is polynomial in O(nk) and hence is polynomial in n. (Most of this circuitry implements the logic of the memory system.) The circuit C consists of at most t = O(nk) copies of M, and hence it has size polynomial in n. The construction of C from x can be accomplished in polynomial time by the reduction algorithm F, since each step of the construction takes polynomial time.
The language CIRCUIT-SAT is therefore at least as hard as any language in NP, and since it belongs to NP, it is NP-complete.
Theorem 36.7
The circuit-satisfiability problem is NP-complete.
Proof Immediate from Lemmas 36.5 and 36.6 and the definition of NP-completeness.
36.3-1
Show that the
36.3-2
Prove that
36.3-3
Show that a satisfying assignment can be used as a certificate in an alternative proof of Lemma 36.5. Which certificate makes for an easier proof?
36.3-4
The proof of Lemma 36.6 assumes that the working storage for algorithm A occupies a contiguous region of polynomial size. Where in the proof is this assumption exploited? Argue that this assumption does not involve any loss of generality.
36.3-5
A language L is complete for a language class C with respect to polynomial-time reductions if L
36.3-6
Show that L is complete for NP if and only if
36.3-7
The reduction algorithm F in the proof of Lemma 36.6 constructs the circuit C = f(x) based on knowledge of x, A, and k. Professor Sartre observes that the string x is input to F, but only the existence of A and k is known to F (since the language L belongs to NP), not their actual values. Thus, the professor concludes that F can't possibly construct the circuit C and that the language CIRCUIT-SAT is not necessarily NP-hard. Explain the flaw in the professor's reasoning.
The NP-completeness of the circuit-satisfiability problem relies on a direct proof that L
The following lemma is the basis of our method for showing that a language is NP-complete.
Lemma 36.8
If L is a language such that L'
Proof Since L' is NP-complete, for all L\"
In other words, by reducing a known NP-complete language L' to L, we implicitly reduce every language in NP to L. Thus, Lemma 36.8 gives us a method for proving that a language L is NP-complete:
1. Prove L
2. Select a known NP-complete language L'.
3. Describe an algorithm that computes a function f mapping every instance of L' to an instance of L.
4. Prove that the function f satisfies x
5. Prove that the algorithm computing f runs in polynomial time.
This methodology of reducing from a single known NP-complete language is far simpler than the more complicated process of providing reductions from every language in NP. Proving CIRCUIT-SAT
We illustrate the reduction methodology by giving an NP-completeness proof for the problem of determining whether a boolean formula, not a circuit, is satisfiable. This problem has the historical honor of being the first problem ever shown to be NP-complete.
We formulate the (formula) satisfiability problem in terms of the language SAT as follows. An instance of SAT is a boolean formula
1. boolean variables: x1, x2, . . . . ;
2. boolean connectives: any boolean function with one or two inputs and one output, such as
3. parentheses.
As in boolean combinational circuits, a truth assignment for a boolean formula
As an example, the formula
has the satisfying assignment
and thus this formula
The naive algorithm to determine whether an arbitrary boolean formula is satisfiable does not run in polynomial time. There are 2n possible assignments in a formula
Theorem 36.9
Satisfiability of boolean formulas is NP-complete.
Proof We shall argue first that SAT
To show that SAT belongs to NP, we show that a certificate consisting of a satisfying assignment for an input formula
To prove that SAT is NP-hard, we show that CIRCUIT-SAT
Unfortunately, this straightforward method does not constitute a polynomial-time reduction. Shared subformulas can cause the size of the generated formula to grow exponentially (see Exercise 36.4-1). Thus, the reduction algorithm must be somewhat more clever.
Figure 36.8 illustrates the basic idea of the reduction from CIRCUIT-SAT to SAT on the circuit from Figure 36.6(a). For each wire xi in the circuit C, the formula
The formula
Given a circuit C, it is straightforward to produce such a formula
Why is the circuit
Many problems can be proved NP-complete by reduction from formula satisfiability. The reduction algorithm must handle any input formula, though, and this can lead to a huge number of cases that must be considered. It is often desirable, therefore, to reduce from a restricted language of boolean formulas, so that fewer cases need be considered. Of course, we must not restrict the language so much that it becomes polynomial-time solvable. One convenient language is 3-CNF satisfiability, or 3-CNF-SAT.
We define 3-CNF satisfiability using the following terms. A literal in a boolean formula is an occurrence of a variable or its negation. A boolean formula is in conjunctive normal form, or CNF, if it is expressed as an AND of clauses, each of which is the OR of one or more literals. A boolean formula is in 3-conjunctive normal form, or 3-CNF, if each clause has exactly three distinct literals.
For example, the boolean formula
is in 3-CNF. The first of its three clauses is (x1
In 3-CNF-SAT, we are asked whether a given boolean formula
Theorem 36.10
Satisfiability of boolean formulas in 3-conjunctive normal form is NP-complete.
Proof The argument we used in the proof of Theorem 36.9 to show that SAT
The reduction algorithm can be broken into three basic steps. Each step progressively transforms the input formula
The first step is similar to the one used to prove CIRCUIT-SAT
Should the input formula contain a clause such as the OR of several literals, associativity can be used to parenthesize the expression fully so that every internal node in the resulting tree has 1 or 2 children. The binary parse tree can now be viewed as a circuit for computing the function.
Mimicking the reduction in the proof of Theorem 36.9, we introduce a variable yi for the output of each internal node. Then, we rewrite the original formula
Observe that the formula
The second step of the reduction converts each clause
In our example, we convert the clause
Applying DeMorgan's laws, we get the CNF formula
which is equivalent to the original clause
Each clause
The third and final step of the reduction further transforms the formula so that each clause has exactly 3 distinct literals. The final 3-CNF formula
We can see that the 3-CNF formula
We must also show that the reduction can be computed in polynomial time. Constructing
36.4-1
Consider the straightforward (nonpolynomial-time) reduction in the proof of Theorem 36.9. Describe a circuit of size n that, when converted to a formula by this method, yields a formula whose size is exponential in n.
36.4-2
Show the 3-CNF formula that results when we use the method of Theorem 36.10 on the formula (36.3).
36.4-3
Professor Jagger proposes to show that SAT
36.4-4
Show that the problem of determining whether a boolean formula is a tautology is complete for co-NP. (Hint: See Exercise 36.3-6.)
36.4-5
Show that the problem of determining the satisfiability of boolean formulas in disjunctive normal form is polynomial-time solvable.
36.4-6
Suppose that someone gives you a polynomial-time algorithm to decide formula satisfiability. Describe how to use this algorithm to find satisfying assignments in polynomial time.
36.4-7
Let 2-CNF-SAT be the set of satisfiable boolean formulas in CNF with exactly 2 literals per clause. Show that 2-CNF-SAT
NP-complete problems arise in diverse domains: boolean logic, graphs, arithmetic, network design, sets and partitions, storage and retrieval, sequencing and scheduling, mathematical programming, algebra and number theory, games and puzzles, automata and language theory, program optimization, and more. In this section, we shall use the reduction methodology to provide NP-completeness proofs for a variety of problems drawn from graph theory and set partitioning.
Figure 36.11 outlines the structure of the NP-completeness proofs in this section and Section 36.4. Each language in the figure is proved NP-complete by reduction from the language that points to it. At the root is CIRCUIT-SAT, which we proved NP-complete in Theorem 36.7.
A clique in an undirected graph G = (V, E) is a subset V'
A naive algorithm for determining whether a graph G = (V, E) with |V| vertices has a clique of size k is to list all k-subsets of V, and check each one to see whether it forms a clique. The running time of this algorithm is
Theorem 36.11
The clique problem is NP-complete.
Proof To show that CLIQUE
We next show that the clique problem is NP-hard by proving that 3-CNF-SAT
The reduction algorithm begins with an instance of 3-CNF-SAT. Let
The graph G = (V, E) is constructed as follows. For each clause
This graph can easily be computed from
then G is the graph shown in Figure 36.12.
We must show that this transformation of
Conversely, suppose that G has a clique V' of size k. No edges in G connect vertices in the same triple, and so V' contains exactly one vertex per triple. We can assign 1 to each literal
In the example of Figure 36.12, a satisfying assignment of
A vertex cover of an undirected graph G = (V, E) is a subset V'
The vertex-cover problem is to find a vertex cover of minimum size in a given graph. Restating this optimization problem as a decision problem, we wish to determine whether a graph has a vertex cover of a given size k. As a language, we define
The following theorem shows that this problem is NP-complete.
Theorem 36.12
The vertex-cover problem is NP-complete.
Proof We first show that VERTEX-COVER
We prove that the vertex-cover problem is NP-hard by showing that CLIQUE
The reduction algorithm takes as input an instance
Suppose that G has a clique V'
Conversely, suppose that
Since VERTEX-COVER is NP-complete, we don't expect to find a polynomial-time algorithm for finding a minimum-size vertex cover. Section 37.1 presents a polynomial-time "approximation algorithm," however, which produces "approximate" solutions for the vertex-cover problem. The size of a vertex cover produced by the algorithm is at most twice the minimum size of a vertex cover.
Thus, we shouldn't give up hope just because a problem is NP-complete. There may be a polynomial-time approximation algorithm that obtains near-optimal solutions, even though finding an optimal solution is NP-complete. Chapter 37 gives several approximation algorithms for NP-complete problems.
The next NP-complete problem we consider is arithmetic. In the subset-sum problem, we are given a finite set S
As usual, we define the problem as a language:
As with any arithmetic problem, it is important to recall that our standard encoding assumes that the input integers are coded in binary. With this assumption in mind, we can show that the subset-sum problem is unlikely to have a fast algorithm.
Theorem 36.13
The subset-sum problem is NP-complete.
Proof To show that SUBSET-SUM is in NP, for an instance
We now show that VERTEX-COVER
At the heart of the reduction is an incidence-matrix representation of G. Let G = (V, E) be an undirected graph and let V = {v0, v1, . . . ,v|V|-1} and E = {e0, e1, . . . , e|E|-1}. The incidence matrix of G is a |V|
For example, Figure 36.14(b) shows the incidence matrix for the undirected graph of Figure 36.14(a). The incidence matrix is shown with lower-indexed edges on the right, rather than on the left as is conventional, in order to simplify the formulas for the numbers in S.
Given a graph G and an integer k, the reduction algorithm computes a set S of numbers and an integer t. To understand how the reduction algorithm works, let us represent numbers in a "modified base-4" fashion. The |E| low-order digits of a number will be in base-4 but the high-order digit can be as large as k. The set of numbers is constructed in such a way that no carries can be propagated from lower digits to higher digits.
The set S consists of two types of numbers, corresponding to vertices and edges respectively. For each vertex vi
For each edge ej
The first digit of the target sum t is k, and all |E| lower-order digits are 2's. Formally,
All of these numbers have polynomial size when we represent them in binary. The reduction can be performed in polynomial time by manipulating the bits of the incidence matrix.
We must now show that graph G has a vertex cover of size k if and only if there is a subset S'
To see that
Now, suppose that there is a subset S'
In Figure 36.14, the vertex cover V' = {v1, v3, v4} corresponds to the subset S' = {x1, x3, x4, y0, y2, y3, y4}. All of the yj are included in S', with the exception of y1, which is incident on two vertices in V'.
We now return to the hamiltonian-cycle problem defined in Section 36.2.
Theorem 36.14
The hamiltonian cycle problem is NP-complete.
Proof We first show that HAM-CYCLE belongs to NP. Given a graph G = (V, E), our certificate is the sequence of |V| vertices that make up the hamiltonian cycle. The verification algorithm checks that this sequence contains each vertex in V exactly once and that with the first vertex repeated at the end, it forms a cycle in G. This verification can be performed in polynomial time.
We now prove that HAM-CYCLE is NP-complete by showing that 3-CNF-SAT
Our first widget is the subgraph A shown in Figure 36.15(a). Suppose that A is a subgraph of some graph G and that the only connections between A and the remainder of G are through the vertices a, a', b, and b'. Furthermore, suppose that graph G has a hamiltonian cycle. Since any hamiltonian cycle of G must pass through vertices z1, z2, z3, and z4 in one of the ways shown in Figures 36.15(b) and (c), we may treat subgraph A as if it were simply a pair of edges (a, a') and (b, b') with the restriction that any hamiltonian cycle of G must include exactly one of these edges. We shall represent widget A as shown in Figure 36.15(d).
The subgraph B in Figure 36.16 is our second widget. Suppose that B is a subgraph of some graph G and that the only connections from B to the remainder of G are through vertices b1, b2, b3, and b4. A hamiltonian cycle of graph G cannot traverse all of the edges (b1, b2), (b2, b3), and (b3, b4), since then all vertices in the widget other than b1, b2, b3, and b4 would be missed. A hamiltonian cycle of G may, however, traverse any proper subset of these edges. Figures 36.16(a)-(e) show five such subsets; the remaining two subsets can be obtained by performing a top-to-bottom flip of parts (b) and (e). We represent this widget as in Figure 36.16(f), the idea being that at least one of the paths pointed to by the arrows must be taken by a hamiltonian cycle.
The graph G that we shall construct consists mostly of copies of these two widgets. The construction is illustrated in Figure 36.17. For each of the k clauses in
Then, for each variable xm in
We are not yet finished with the construction of graph G, since we have yet to relate the variables to the clauses. If the jth literal of clause Ci is xm, then we use an A widget to connect edge (bij, bi,j+1) with edge em. If the jth literal of clause Ci is
Note that connecting two edges by means of A widgets actually entails replacing each edge by the five edges in the top or bottom of Figure 36.15(a) and, of course, adding the connections that pass through the z vertices as well. A given literal lm may appear in several clauses (
We claim that formula
(It actually traverses edges within the A widgets as well, but we use these subgraphs to enforce the either/or nature of the edges it connects.)
Given the hamiltonian cycle h, we define a truth assignment for
We claim that this assignment satisfies
Conversely, let us suppose that formula ø is satisfied by some truth assignment. By following the rules from above, we can construct a hamiltonian cycle for graph G: traverse edge em if xm = 1, traverse edge
Finally, we note that graph G can be constructed in polynomial time. It contains one B widget for each of the k clauses in ø. There is one A widget for each instance of each literal in ø, and so there are 3k A widgets. Since the A and B widgets are of fixed size, the graph G has O(k) vertices and edges and is easily constructed in polynomial time. Thus, we have provided a polynomial-time reduction from 3-CNF-SAT to HAM-CYCLE.
In the traveling-salesman problem, which is closely related to the hamiltonian-cycle problem, a salesman must visit n cities. Modeling the problem as a complete graph with n vertices, we can say that the salesman wishes to make a tour, or hamiltonian cycle, visiting each city exactly once and finishing at the city he starts from. There is an integer cost c(i, j) to travel from city i to city j, and the salesman wishes to make the tour whose total cost is minimum, where the total cost is the sum of the individual costs along the edges of the tour. For example, in Figure 36.19, a minimum-cost tour is
The following theorem shows that a fast algorithm for the traveling-salesman problem is unlikely to exist.
Theorem 36.15
The traveling-salesman problem is NP-complete.
Proof We first show that TSP belongs to NP. Given an instance of the problem, we use as a certificate the sequence of n vertices in the tour. The verification algorithm checks that this sequence contains each vertex exactly once, sums up the edge costs, and checks whether the sum is at most k. This process can certainly be done in polynomial time.
To prove that TSP is NP-hard, we show that HAM-CYCLE
The instance of TSP is then (G', c, 0), which is easily formed in polynomial time.
We now show that graph G has a hamiltonian cycle if and only if graph G' has a tour of cost at most 0. Suppose that graph G has a hamiltonian cycle h. Each edge in h belongs to E and thus has cost 0 in G'. Thus, h is a tour in G' with cost 0. Conversely, suppose that graph G' has a tour h' of cost at most 0. Since the costs of the edges in E' are 0 and 1, the cost of tour h' is exactly 0. Therefore, h' contains only edges in E. We conclude that h is a hamiltonian cycle in graph G.
36.5-1
The subgraph-isomorphism problem takes two graphs G1 and G2 and asks whether G1 is a subgraph of G2. Show that the subgraph-isomorphism problem is NP-complete.
36.5-2
Given an integer m-by-n matrix A and an integer m-vector b, the 0-1 integer-programming problem asks whether there is an integer n-vector x with elements in the set {0,1} such that Ax
36.5-3
Show that the subset-sum problem is solvable in polynomial time if the target value t is expressed in unary.
36.5-4
The set-partition problem takes as input a set S of numbers. The question is whether the numbers can be partitioned into two sets A and
36.5-5
Show that the hamiltonian-path problem is NP-complete.
36.5-6
The longest-simple-cycle problem is the problem of determining a simple cycle (no repeated vertices) of maximum length in a graph. Show that this problem is NP-complete.
36.5-7
Professor Marconi proclaims that the subgraph used as widget A in the proof of Theorem 36.14 is more complicated than necessary: vertices z3 and z4 of Figure 36.15(a) and the vertices above and below them are not needed. Is the professor correct? That is, does the reduction work with this smaller version of the widget, or does the "either/or" property of the widget disappear?
36-1 Independent set
An independent set of a graph G = (V,E) is a subset V'
a. Formulate a related decision problem for the independent-set problem, and prove that it is NP-complete. (Hint: Reduce from the clique problem.)
b. Suppose that you are given a subroutine to solve the decision problem you defined in part (a). Give an algorithm to find an independent set of maximum size. The running time of your algorithm should be polynomial in |V| and |E|, where queries to the black box are counted as a single step.
Although the independent-set decision problem is NP-complete, certain special cases are polynomial-time solvable.
c. Give an efficient algorithm to solve the independent-set problem when each vertex in G has degree 2. Analyze the running time, and prove that your algorithm works correctly.
d. Give an efficient algorithm to solve the independent-set problem when G is bipartite. Analyze the running time, and prove that your algorithm works correctly. (Hint: Use the results of Section 27.3.)
36-2 Graph coloring
A k-coloring of an undirected graph G = (V,E) is a function c : V
a. Give an efficient algorithm to determine a 2-coloring of a graph if one exists.
b. Cast the graph-coloring problem as a decision problem. Show that your decision problem is solvable in polynomial time if and only if the graph-coloring problem is solvable in polynomial time.
c. Let the language 3-COLOR be the set of graphs that can be 3-colored. Show that if 3-COLOR is NP-complete, then your decision problem from part (b) is NP-complete.
To prove that 3-COLOR is NP-complete, we use a reduction from 3-CNF-SAT. Given a formula ø of m clauses on n variables x1, x2, . . . , xn, we construct a graph G = (V,E) as follows. The set V consists of a vertex for each variable, a vertex for the negation of each variable, 5 vertices for each clause, and 3 special vertices: TRUE, FALSE, and RED. The edges of the graph are of two types: "literal" edges that are independent of the clauses and "clause" edges that depend on the clauses. The literal edges form a triangle on the special vertices and also form a triangle on xi,
d. Argue that in any 3-coloring c of a graph containing the literal edges, exactly one of a variable and its negation is colored c(TRUE) and the other is colored c(FALSE). Argue that for any truth assignment for ø, there is a 3-coloring of the graph containing just the literal edges.
The widget shown in Figure 36.20 is used to enforce the condition corresponding to a clause (x V y V z). Each clause requires a unique copy of the 5 vertices that are heavily shaded in the figure; they connect as shown to the literals of the clause and the special vertex TRUE.
e. Argue that if each of x, y, and z is colored c(TRUE) or c(FALSE), then the widget is 3-colorable if and only if at least one of x, y, or z is colored c(TRUE).
f. Complete the proof that 3-COLOR is NP-complete.
Garey and Johnson [79] provide a wonderful guide to NP-completeness, discussing the theory at length and providing a catalogue of many problems that were known to be NP-complete in 1979. (The list of NP-complete problem domains at the beginning of Section 36.5 is drawn from their table of contents.) Hopcroft and Ullman [104] and Lewis and Papadimitriou [139] have good treatments of NP-completeness in the context of complexity theory. Aho, Hopcroft, and Ullman [4] also cover NP-completeness and give several reductions, including a reduction for the vertex-cover problem from the hamiltonian-cycle problem.
The class P was introduced in 1964 by Cobham [44] and, independently, in 1965 by Edmonds [61], who also introduced the class NP and conjectured that P
The proof of Theorem 36.14 was adapted from Papadimitriou and Steiglitz [154].
 V, and a nonnegative integer k, does a path exist in G between u and v whose length is at most k?" If i = <G, u, v, k> is an instance of this shortest-path problem, then PATH(i) = 1 (yes) if a shortest path from u to v has length at most k, and PATH(i) = 0 (no) otherwise.
V, and a nonnegative integer k, does a path exist in G between u and v whose length is at most k?" If i = <G, u, v, k> is an instance of this shortest-path problem, then PATH(i) = 1 (yes) if a shortest path from u to v has length at most k, and PATH(i) = 0 (no) otherwise.Encodings
 {0, 1}* can be used to induce a related concrete decision problem, which we denote by e(Q). If the solution to an abstract-problem instance i
{0, 1}* can be used to induce a related concrete decision problem, which we denote by e(Q). If the solution to an abstract-problem instance i  I is Q(i)
I is Q(i)  {0, 1}, then the solution to the concrete-problem instance e(i)
{0, 1}, then the solution to the concrete-problem instance e(i)  {0, 1}* is also Q(i). As a technicality, there may be some binary strings that represent no meaningful abstract-problem instance. For convenience, we shall assume that any such string is mapped arbitrarily to 0. Thus, the concrete problem produces the same solutions as the abstract problem on binary-string instances that represent the encodings of abstract-problem instances.
{0, 1}* is also Q(i). As a technicality, there may be some binary strings that represent no meaningful abstract-problem instance. For convenience, we shall assume that any such string is mapped arbitrarily to 0. Thus, the concrete problem produces the same solutions as the abstract problem on binary-string instances that represent the encodings of abstract-problem instances. (k). If the integer k is provided in unary--a string of k 1's--then the running time of the algorithm is O(n) on length-n inputs, which is polynomial time. If we use the more natural binary representation of the integer k, however, then the input length is n =
(k). If the integer k is provided in unary--a string of k 1's--then the running time of the algorithm is O(n) on length-n inputs, which is polynomial time. If we use the more natural binary representation of the integer k, however, then the input length is n =  lg k
lg k . In this case, the running time of the algorithm is
. In this case, the running time of the algorithm is  (k) =
(k) =  (2n), which is exponential in the size of the input. Thus, depending on the encoding, the algorithm runs in either polynomial or superpolynomial time.
(2n), which is exponential in the size of the input. Thus, depending on the encoding, the algorithm runs in either polynomial or superpolynomial time. {0, 1}* is polynomial-time computable if there exists a polynomial-time algorithm A that, given any input x
{0, 1}* is polynomial-time computable if there exists a polynomial-time algorithm A that, given any input x  {0, 1}*, produces as output f(x). For some set I of problem instances, we say that two encodings e and e are polynomially related if there exist two polynomial-time computable functions f12 and f21 such that for any i
{0, 1}*, produces as output f(x). For some set I of problem instances, we say that two encodings e and e are polynomially related if there exist two polynomial-time computable functions f12 and f21 such that for any i  I, we have f12(e1(i)) = e2(i) and f21(e2(i)) = e1(i). That is, the encoding e2(i) can be computed from the encoding e1(i) by a polynomial-time algorithm, and vice versa. If two encodings e1 and e2 of an abstract problem are polynomially related, which we use makes no difference to whether the problem is polynomial-time solvable or not, as the following lemma shows.
I, we have f12(e1(i)) = e2(i) and f21(e2(i)) = e1(i). That is, the encoding e2(i) can be computed from the encoding e1(i) by a polynomial-time algorithm, and vice versa. If two encodings e1 and e2 of an abstract problem are polynomially related, which we use makes no difference to whether the problem is polynomial-time solvable or not, as the following lemma shows. P if and only if e2(Q)
P if and only if e2(Q)  P.
P. G
G denotes the standard encoding of a graph G.
denotes the standard encoding of a graph G.A formal-language framework
 is a finite set of symbols. A language L over
is a finite set of symbols. A language L over  is any set of strings made up of symbols from
is any set of strings made up of symbols from  . For example, if
. For example, if  = {0, 1}, the set L = {10, 11, 101, 111, 1011, 1101, 10001, . . .} is the language of binary representations of prime numbers. We denote the empty string by
= {0, 1}, the set L = {10, 11, 101, 111, 1011, 1101, 10001, . . .} is the language of binary representations of prime numbers. We denote the empty string by  , and the empty language by
, and the empty language by  . The language of all strings over
. The language of all strings over  is denoted
is denoted  *. For example, if
*. For example, if  = {0, 1}, then
= {0, 1}, then  * = {
* = { , 0, 1, 00, 01, 10, 11, 000, . . .} is the set of all binary strings. Every language L over
, 0, 1, 00, 01, 10, 11, 000, . . .} is the set of all binary strings. Every language L over  is a subset of
is a subset of  *.
*. . The concatenation of two languages L1 and L2 is the language
. The concatenation of two languages L1 and L2 is the languageL = {x1x2 : x1  L1 and x2
L1 and x2  L2} .
L2} .L* = { }
}  L
L  L2
L2  L3
L3  . . ,
. . , *, where
*, where  = {0, 1}. Since Q is entirely characterized by those problem instances that produce a 1 (yes) answer, we can view Q as a language L over
= {0, 1}. Since Q is entirely characterized by those problem instances that produce a 1 (yes) answer, we can view Q as a language L over  = {0, 1}, where
= {0, 1}, whereL = {x 
 * : Q(x) = 1} .
* : Q(x) = 1} .PATH = {
 G,u,v,k
G,u,v,k : G = (V,E) is an undirected graph,
: G = (V,E) is an undirected graph,u,v
 V,
V,k
 0 is an integer, and
0 is an integer, andthere exists a path from u to v in G
whose length is at most k}.
 {0, 1}* if, given input x, the algorithm outputs A(x) = 1. The language accepted by an algorithm A is the set L = {x
{0, 1}* if, given input x, the algorithm outputs A(x) = 1. The language accepted by an algorithm A is the set L = {x  {0, 1}* : A(x) = 1}, that is, the set of strings that the algorithm accepts. An algorithm A rejects a string x if A(x) = 0.
{0, 1}* : A(x) = 1}, that is, the set of strings that the algorithm accepts. An algorithm A rejects a string x if A(x) = 0. L provided as input to it. For example, the algorithm may loop forever. A language L is decided by an algorithm A if every binary string is either accepted or rejected by the algorithm. A language L is accepted in polynomial time by an algorithm A if for any length-n string x
L provided as input to it. For example, the algorithm may loop forever. A language L is decided by an algorithm A if every binary string is either accepted or rejected by the algorithm. A language L is accepted in polynomial time by an algorithm A if for any length-n string x  L, the algorithm accepts x in time O(nk) for some constant k. A language L is decided in polynomial time by an algorithm A if for any length-n string x
L, the algorithm accepts x in time O(nk) for some constant k. A language L is decided in polynomial time by an algorithm A if for any length-n string x  {0, 1 }*, the algorithm decides x in time O(nk) for some constant k. Thus, to accept a language, an algorithm need only worry about strings in L, but to decide a language, it must accept or reject every string in {0, 1}*.
{0, 1 }*, the algorithm decides x in time O(nk) for some constant k. Thus, to accept a language, an algorithm need only worry about strings in L, but to decide a language, it must accept or reject every string in {0, 1}*.P = {L  {0,1}* : there exists an algorithm A
{0,1}* : there exists an algorithm Athat decides L in polynomial time} .
 P, we may not actually know a bound on the running time for the algorithm A that accepts L. Nevertheless, we know that such a bound exists, and therefore, that an algorithm A' exists that can check the bound, even though we may not be able to find the algorithm A' easily.
P, we may not actually know a bound on the running time for the algorithm A that accepts L. Nevertheless, we know that such a bound exists, and therefore, that an algorithm A' exists that can check the bound, even though we may not be able to find the algorithm A' easily.Exercises
 G, u, v, k
G, u, v, k : G = (V, E) is an undirected graph, u, v
: G = (V, E) is an undirected graph, u, v  V, k
V, k  0 is an integer, and there exists a simple path from u to v in G whose length is at least k}. Show that the optimization problem LONGEST-PATH-LENGTH can be solved in polynomial time if and only if LONGEST-PATH
0 is an integer, and there exists a simple path from u to v in G whose length is at least k}. Show that the optimization problem LONGEST-PATH-LENGTH can be solved in polynomial time if and only if LONGEST-PATH  P.
P. L in polynomial time, but that the algorithm that does this runs in superpolynomial time if x
L in polynomial time, but that the algorithm that does this runs in superpolynomial time if x  L. Argue that L can be decided in polynomial time.
L. Argue that L can be decided in polynomial time. P, then Ll
P, then Ll  L2
L2  P, etc.
P, etc.36.2 Polynomial-time verification
 G, u, v, k
G, u, v, k of the decision problem PATH, we are also given a path p from u to v. We can easily check whether the length of p is at most k, and if so, we can view p as a "certificate" that the instance indeed belongs to PATH. For the decision problem PATH, this certificate doesn't seem to buy us much. After all, PATH belongs to P--in fact, PATH can be solved in linear time--and so verifying membership from a given certificate takes as long as solving the problem from scratch. We shall now examine a problem for which we know of no polynomial-time decision algorithm yet, given a certificate, verification is easy.
of the decision problem PATH, we are also given a path p from u to v. We can easily check whether the length of p is at most k, and if so, we can view p as a "certificate" that the instance indeed belongs to PATH. For the decision problem PATH, this certificate doesn't seem to buy us much. After all, PATH belongs to P--in fact, PATH can be solved in linear time--and so verifying membership from a given certificate takes as long as solving the problem from scratch. We shall now examine a problem for which we know of no polynomial-time decision algorithm yet, given a certificate, verification is easy.
Figure 36.1 (a) A graph representing the vertices, edges, and faces of a dodecahedron, with a hamiltonian cycle shown by shaded edges. (b) A bipartite graph with an odd number of vertices. Any such graph is nonhamiltonian.
Hamiltonian cycles
HAM-CYCLE = {
 G
G : G is a hamiltonian graph} .
: G is a hamiltonian graph} . G
G , one possible decision algorithm lists all permutations of the vertices of G and then checks each permutation to see if it is a hamiltonian path. What is the running time of this algorithm? If we use the "reasonable" encoding of a graph as its adjacency matrix, the number m of vertices in the graph is
, one possible decision algorithm lists all permutations of the vertices of G and then checks each permutation to see if it is a hamiltonian path. What is the running time of this algorithm? If we use the "reasonable" encoding of a graph as its adjacency matrix, the number m of vertices in the graph is  , where n = |
, where n = | G
G | is the length of the encoding of G. There are m! possible permutations of the vertices, and therefore the running time is
| is the length of the encoding of G. There are m! possible permutations of the vertices, and therefore the running time is  , which is not O(nk) for any constant k. Thus, this naive algorithm does not run in polynomial time, and in fact, the hamiltonian-cycle problem is NP-complete, as we shall prove in Section 36.5.
, which is not O(nk) for any constant k. Thus, this naive algorithm does not run in polynomial time, and in fact, the hamiltonian-cycle problem is NP-complete, as we shall prove in Section 36.5.Verification algorithms
L = {x  {0, 1}* : there exists y
{0, 1}* : there exists y  {0, 1}* such that A(x, y) = 1} .
{0, 1}* such that A(x, y) = 1} . L, there is a certificate y that A can use to prove that x
L, there is a certificate y that A can use to prove that x  L. Moreover, for any string x
L. Moreover, for any string x  L there must be no certificate proving that x
L there must be no certificate proving that x  L. For example, in the hamiltonian-cycle problem, the certificate is the list of vertices in the hamiltonian cycle. If a graph is hamiltonian, the hamiltonian cycle itself offers enough information to verify this fact. Conversely, if a graph is not hamiltonian, there is no list of vertices that can fool the verification algorithm into believing that the graph is hamiltonian, since the verification algorithm carefully checks the proposed "cycle" to be sure.
L. For example, in the hamiltonian-cycle problem, the certificate is the list of vertices in the hamiltonian cycle. If a graph is hamiltonian, the hamiltonian cycle itself offers enough information to verify this fact. Conversely, if a graph is not hamiltonian, there is no list of vertices that can fool the verification algorithm into believing that the graph is hamiltonian, since the verification algorithm carefully checks the proposed "cycle" to be sure.The complexity class NP
L = {x  {0,1}* : there exists a certificate y with |y| = 0(|x|c)
{0,1}* : there exists a certificate y with |y| = 0(|x|c)such that A(x,y) = 1} .
 NP. (It is always nice to know that an important set is nonempty.) Moreover, if L
NP. (It is always nice to know that an important set is nonempty.) Moreover, if L  P, then L
P, then L  NP, since if there is a polynomial-time algorithm to decide L, the algorithm can be easily converted to a two-argument verification algorithm that simply ignores any certificate and accepts exactly those input strings it determines to be in L. Thus, P
NP, since if there is a polynomial-time algorithm to decide L, the algorithm can be easily converted to a two-argument verification algorithm that simply ignores any certificate and accepts exactly those input strings it determines to be in L. Thus, P  NP.
NP. NP--the existence of "NP-complete" languages. We shall study this class in Section 36.3.
NP--the existence of "NP-complete" languages. We shall study this class in Section 36.3. NP question remain unresolved. Despite much work by many researchers, no one even knows if the class NP is closed under complement. That is, does L
NP question remain unresolved. Despite much work by many researchers, no one even knows if the class NP is closed under complement. That is, does L  NP imply
NP imply  ? We can define the complexity class co-NP as the set of languages L such that
? We can define the complexity class co-NP as the set of languages L such that  . The question of whether NP is closed under complement can be rephrased as whether NP = co-NP. Since P is closed under complement (Exercise 36.1-7), it follows that P
. The question of whether NP is closed under complement can be rephrased as whether NP = co-NP. Since P is closed under complement (Exercise 36.1-7), it follows that P  NP
NP  co-NP. Once again, however, it is not known whether P = NP
co-NP. Once again, however, it is not known whether P = NP  co-NP or whether there is some language in NP
co-NP or whether there is some language in NP  co-NP - P. Figure 36.2 shows the four possible scenarios.
co-NP - P. Figure 36.2 shows the four possible scenarios.
Figure 36.2 Four possibilities for relationships among complexity classes. In each diagram, one region enclosing another indicates a proper-subset relation. (a) P = NP = co-NP. Most researchers regard this possibility as the most unlikely. (b) If NP is closed under complement, then NP = co-NP, but it need not be the case that P = NP. (c) P = NP
 co-NP, but NP is not closed under complement. (d) NP
co-NP, but NP is not closed under complement. (d) NP  co-NP and P
co-NP and P  NP
NP  co-NP. Most researchers regard this possibility as the most likely.
co-NP. Most researchers regard this possibility as the most likely.Exercises
 G1, G2
G1, G2 : G1 and G2 are isomorphic graphs}. Prove that GRAPH-ISOMORPHISM
: G1 and G2 are isomorphic graphs}. Prove that GRAPH-ISOMORPHISM  NP by describing a polynomial-time algorithm to verify the language.
NP by describing a polynomial-time algorithm to verify the language. P, then the problem of listing the vertices of a hamiltonian cycle, in order, is polynomial-time solvable.
P, then the problem of listing the vertices of a hamiltonian cycle, in order, is polynomial-time solvable. G, u, v
G, u, v : there is a hamiltonian path from u to v in graph G} belongs to NP.
: there is a hamiltonian path from u to v in graph G} belongs to NP. be a boolean formula constructed from the boolean input variables x1, x2, . . . , xk, negations (
be a boolean formula constructed from the boolean input variables x1, x2, . . . , xk, negations ( ), AND's (
), AND's ( ), OR's (
), OR's ( ), and parentheses. The formula
), and parentheses. The formula  is a tautology if it evaluates to 1 for every assignment of 1 and 0 to the input variables. Define TAUTOLOGY as the language of boolean formulas that are tautologies. Show that TAUTOLOGY
is a tautology if it evaluates to 1 for every assignment of 1 and 0 to the input variables. Define TAUTOLOGY as the language of boolean formulas that are tautologies. Show that TAUTOLOGY  co-NP.
co-NP. co-NP.
co-NP. co-NP, then P
co-NP, then P  NP.
NP.36.3 NP-completeness and reducibility
 NP is the existence of the class of "NP-complete" problems. This class has the surprising property that if any one NP-complete problem can be solved in polynomial time, then every problem in NP has a polynomial-time solution, that is, P = NP. Despite years of study, though, no polynomial-time algorithm has ever been discovered for any NP-complete problem.
NP is the existence of the class of "NP-complete" problems. This class has the surprising property that if any one NP-complete problem can be solved in polynomial time, then every problem in NP has a polynomial-time solution, that is, P = NP. Despite years of study, though, no polynomial-time algorithm has ever been discovered for any NP-complete problem. NP - P.
NP - P.
Figure 36.3 An illustration of a polynomial-time reduction from a language L1 to a language L2 via a reduction function f. For any input x
 {0, 1}*, the question of whether x
{0, 1}*, the question of whether x  L1 has the same answer as the question of whether f(x)
L1 has the same answer as the question of whether f(x)  L2.
L2.Reducibility
 P L2, if there exists a polynomial-time computable function f : {0, 1}*
P L2, if there exists a polynomial-time computable function f : {0, 1}*  {0, 1}* such that for all x
{0, 1}* such that for all x  {0, 1}*,
{0, 1}*,x
 L1 if and only if f(x)
L1 if and only if f(x)  L2 .
L2 .(36.1)
 L1, then f(x)
L1, then f(x)  L2. Moreover, if x
L2. Moreover, if x  L1, then f(x)
L1, then f(x)  L2. Thus, the reduction function maps any instance x of the decision problem represented by the language L1 to an instance f(x) of the problem represented by L2. Providing an answer to whether f(x)
L2. Thus, the reduction function maps any instance x of the decision problem represented by the language L1 to an instance f(x) of the problem represented by L2. Providing an answer to whether f(x)  L2 directly provides the answer to whether x
L2 directly provides the answer to whether x  L1.
L1.
Figure 36.4 The proof of Lemma 36.3. The algorithm F is a reduction algorithm that computes the reduction function f from L1 to L2 in polynomial time, and A2 is a polynomial-time algorithm that decides L2. Illustrated is an algorithm A1 that decides whether x
 L1 by using F to transform any input x into f(x) and then using A2 to decide whether f(x)
L1 by using F to transform any input x into f(x) and then using A2 to decide whether f(x)  L2.
L2. {0, 1}* are languages such that L1
{0, 1}* are languages such that L1  L2, then L2
L2, then L2  P implies L1
P implies L1  P.
P. {0, 1}*, the algorithm A1 uses F to transform x into f(x), and then it uses A2 to test whether f(x)
{0, 1}*, the algorithm A1 uses F to transform x into f(x), and then it uses A2 to test whether f(x)  L2. The output of A2 is the value provided as the output from A1.
L2. The output of A2 is the value provided as the output from A1.NP-completeness
 p L2, then L1 is not more than a polynomial factor harder than L2, which is why the "less than or equal to" notation for reduction is mnemonic. We can now define the set of NP-complete languages, which are the hardest problems in NP.
p L2, then L1 is not more than a polynomial factor harder than L2, which is why the "less than or equal to" notation for reduction is mnemonic. We can now define the set of NP-complete languages, which are the hardest problems in NP. {0, 1}* is NP-complete if
{0, 1}* is NP-complete if NP, and
NP, and p L for every L'
p L for every L'  NP.
NP.
Figure 36.5 How most theoretical computer scientists view the relationships among P, NP, and NPC. Both P and NPC are wholly contained within NP, and
 .
. P and also that L
P and also that L  NPC. For any L'
NPC. For any L'  NP, we have L'
NP, we have L'  p L by property 2 of the definition of NP-completeness. Thus, by Lemma 36.3, we also have that L'
p L by property 2 of the definition of NP-completeness. Thus, by Lemma 36.3, we also have that L'  P, which proves the first statement of the lemma.
P, which proves the first statement of the lemma. NP such that L
NP such that L  P. Let L'
P. Let L'  NPC be any NP-complete language, and for the purpose of contradiction, assume that L'
NPC be any NP-complete language, and for the purpose of contradiction, assume that L'  P. But then, by Lemma 36.3, we have L
P. But then, by Lemma 36.3, we have L  p L', and thus L
p L', and thus L  P.
P.  NP question centers around the NP-complete problems. Most theoretical computer scientists believe that P
NP question centers around the NP-complete problems. Most theoretical computer scientists believe that P  NP, which leads to the relationships among P, NP, and NPC shown in Figure 36.5. But for all we know, someone may come up with a polynomial-time algorithm for an NP-complete problem, thus proving that P = NP. Nevertheless, since no polynomial-time algorithm for any NP-complete problem has yet been discovered, a proof that a problem is NP-compete provides excellent evidence for its intractability.
NP, which leads to the relationships among P, NP, and NPC shown in Figure 36.5. But for all we know, someone may come up with a polynomial-time algorithm for an NP-complete problem, thus proving that P = NP. Nevertheless, since no polynomial-time algorithm for any NP-complete problem has yet been discovered, a proof that a problem is NP-compete provides excellent evidence for its intractability.Circuit satisfiability

Figure 36.6 Two instances of the circuit-satisfiability problem. (a) The assignment
 x1 = 1, x2 = 1, x3 = 0
x1 = 1, x2 = 1, x3 = 0 to the inputs of this circuit causes the output of the circuit to be 1. The circuit is therefore satisfiable. (b) No assignment to the inputs of this circuit can cause the output of the circuit to be 1. The circuit is therefore unsatisfiable.
to the inputs of this circuit causes the output of the circuit to be 1. The circuit is therefore satisfiable. (b) No assignment to the inputs of this circuit can cause the output of the circuit to be 1. The circuit is therefore unsatisfiable. x1 = 1, x2 = 1, x3 = 0
x1 = 1, x2 = 1, x3 = 0 , and so it is satisfiable. No assignment of values to x1, x2, and x3 causes the circuit in Figure 36.6(b) to produce a 1 output; it always produces 0, and so it is unsatisfiable.
, and so it is satisfiable. No assignment of values to x1, x2, and x3 causes the circuit in Figure 36.6(b) to produce a 1 output; it always produces 0, and so it is unsatisfiable. C
C whose length is not much larger than the size of the circuit itself. As a formal language, we can therefore define
whose length is not much larger than the size of the circuit itself. As a formal language, we can therefore defineCIRCUIT-SAT =
{ C
C : C is a satisfiable boolean combinational circuit} .
: C is a satisfiable boolean combinational circuit} . NP.
NP.  L if and only if C
L if and only if C  CIRCUIT-SAT.
CIRCUIT-SAT. NP, there must exist an algorithm A that verifies L in polynomial-time. The algorithm F that we shall construct will use the two-input algorithm A to compute the reduction function â.
NP, there must exist an algorithm A that verifies L in polynomial-time. The algorithm F that we shall construct will use the two-input algorithm A to compute the reduction function â. 1 be a constant such that T(n) = O(nk) and the length of the certificate is O(nk). (The running time of A is actually a polynomial in the total input size, which includes both an input string and a certificate, but since the length of the certificate is polynomial in the length n of the input string, the running time is polynomial in n.)
1 be a constant such that T(n) = O(nk) and the length of the certificate is O(nk). (The running time of A is actually a polynomial in the total input size, which includes both an input string and a certificate, but since the length of the certificate is polynomial in the length n of the input string, the running time is polynomial in n.)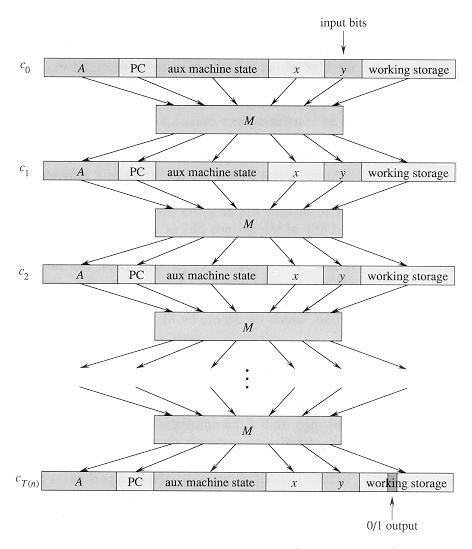
Figure 36.7 The sequence of configurations produced by an algorithm A running on an input x and certificate y. Each configuration represents the state of the computer for one step of the computation and, besides A, x, and y, includes the program counter (PC), auxiliary machine state, and working storage. Except for the certificate y, the initial configuration c0 is constant. Each configuration is mapped to the next configuration by a boolean combinational circuit M. The output is a distinguished bit in the working storage.
Exercises
 p relation is a transitive relation on languages. That is, show that if L1
p relation is a transitive relation on languages. That is, show that if L1  p L2 and L2
p L2 and L2  p L3, then L1
p L3, then L1  p L3.
p L3. if and only if
if and only if  .
. C and L'
C and L'  p L for all L'
p L for all L' C. Show that
C. Show that  and {0, 1}* are the only languages in P that are not complete for P with respect to polynomial-time reductions.
and {0, 1}* are the only languages in P that are not complete for P with respect to polynomial-time reductions. is complete for co-NP.
is complete for co-NP.36.4 NP-completeness proofs
 P CIRCUIT-SAT for every language L
P CIRCUIT-SAT for every language L  NP. In this section, we shall show how to prove that languages are NP-complete without directly reducing every language in NP to the given language. We shall illustrate this methodology by proving that various formula-satisfiability problems are NP-complete. Section 36.5 provides many more examples of the methodology.
NP. In this section, we shall show how to prove that languages are NP-complete without directly reducing every language in NP to the given language. We shall illustrate this methodology by proving that various formula-satisfiability problems are NP-complete. Section 36.5 provides many more examples of the methodology. p L for some L'
p L for some L'  NPC, then L is NP-hard. Moreover, if L
NPC, then L is NP-hard. Moreover, if L  NP, then L
NP, then L  NPC.
NPC. NP, we have L\"
NP, we have L\"  p L'. By supposition, L'
p L'. By supposition, L'  p L, and thus by transitivity (Exercise 36.3-1), we have L\"
p L, and thus by transitivity (Exercise 36.3-1), we have L\"  p L, which shows that L is NP-hard. If L
p L, which shows that L is NP-hard. If L  NP, we also have L
NP, we also have L  NPC.
NPC.  NP.
NP. L' if and only if f(x)
L' if and only if f(x)  L for all x
L for all x  {0, 1 }*.
{0, 1 }*. NPC has given us a "foot in the door." Knowing that the circuit-satisfiability problem is NP-complete now allows us to prove much more easily that other problems are NP-complete. Moreover, as we develop a catalog of known NP-complete problems, applying the methodology will become that much easier.
NPC has given us a "foot in the door." Knowing that the circuit-satisfiability problem is NP-complete now allows us to prove much more easily that other problems are NP-complete. Moreover, as we develop a catalog of known NP-complete problems, applying the methodology will become that much easier.Formula satisfiability
 composed of
composed of (AND),
(AND),  (OR),
(OR),  (NOT),
(NOT),  (implication),
(implication),  (if and only if); and
(if and only if); and is a set of values for the variables of
is a set of values for the variables of  , and a satisfying assignment is a truth assignment that causes it to evaluate to 1. A formula with a satisfying assignment is a satisfiable formula. The satisfiability problem asks whether a given boolean formula is satisfiable; in formal-language terms,
, and a satisfying assignment is a truth assignment that causes it to evaluate to 1. A formula with a satisfying assignment is a satisfiable formula. The satisfiability problem asks whether a given boolean formula is satisfiable; in formal-language terms,SAT = {


 :
:  is a satisfiable boolean formula} .
is a satisfiable boolean formula} . = ((x1
= ((x1  x2)
x2) 
 ((
(( x1
x1  x3)
x3)  x4))
x4)) 
 x2
x2 x1 = 0, x2 = 0, x3 = 1, x4 = 1
x1 = 0, x2 = 0, x3 = 1, x4 = 1 , since
, since = ((0
= ((0  0)
0) 
 ((
(( 0
0  1)
1)  1))
1)) 
 0
0= (1

 (1
(1  1))
1))  1
1= (1
 0)
0)  1
1= 1 ,
(36.2)
 belongs to SAT.
belongs to SAT. with n variables. If the length of
with n variables. If the length of 

 is polynomial in n, then checking every assignment requires superpolynomial time. As the following theorem shows, a polynomial-time algorithm is unlikely to exist.
is polynomial in n, then checking every assignment requires superpolynomial time. As the following theorem shows, a polynomial-time algorithm is unlikely to exist.
Figure 36.8 Reducing circuit satisfiability to formula satisfiability. The formula produced by the reduction algorithm has a variable for each wire in the circuit.
 NP. Then, we shall show that CIRCUIT-SAT
NP. Then, we shall show that CIRCUIT-SAT  p SAT; by Lemma 36.8, this will prove the theorem.
p SAT; by Lemma 36.8, this will prove the theorem. can be verified in polynomial time. The verifying algorithm simply replaces each variable in the formula with its corresponding value and then evaluates the expression, much as we did in equation (36.2) above. This task is easily doable in polynomial time. If the expression evaluates to 1, the formula is satisfiable. Thus, the first condition of Lemma 36.8 for NP-completeness holds.
can be verified in polynomial time. The verifying algorithm simply replaces each variable in the formula with its corresponding value and then evaluates the expression, much as we did in equation (36.2) above. This task is easily doable in polynomial time. If the expression evaluates to 1, the formula is satisfiable. Thus, the first condition of Lemma 36.8 for NP-completeness holds. p SAT. In other words, any instance of circuit satisfiability can be reduced in polynomial time to an instance of formula satisfiability. Induction can be used to express any boolean combinational circuit as a boolean formula. We simply look at the gate that produces the circuit output and inductively express each of the gate's inputs as formulas. The formula for the circuit is then obtained by writing an expression that applies the gate's function to its inputs' formulas.
p SAT. In other words, any instance of circuit satisfiability can be reduced in polynomial time to an instance of formula satisfiability. Induction can be used to express any boolean combinational circuit as a boolean formula. We simply look at the gate that produces the circuit output and inductively express each of the gate's inputs as formulas. The formula for the circuit is then obtained by writing an expression that applies the gate's function to its inputs' formulas. has a variable xi. The proper operation of a gate can now be expressed as a formula involving the variables of its incident wires. For example, the operation of the output AND gate is x10
has a variable xi. The proper operation of a gate can now be expressed as a formula involving the variables of its incident wires. For example, the operation of the output AND gate is x10  (x7
(x7  x8
x8  x9).
x9). produced by the reduction algorithm is the AND of the circuit-output variable with the conjunction of clauses describing the operation of each gate. For the circuit in the figure, the formula is
produced by the reduction algorithm is the AND of the circuit-output variable with the conjunction of clauses describing the operation of each gate. For the circuit in the figure, the formula is = x10
= x10  (x4
(x4 
 x3)
x3) (x5
(x5  (x1
(x1  x2))
x2)) (x6
(x6 
 x4)
x4) (x7
(x7  (x1
(x1  x2
x2  x4))
x4)) (x8
(x8  (x5
(x5  x6))
x6)) (x9
(x9  (x6
(x6  x7))
x7)) (x10
(x10  (x7
(x7  x8
x8  x9)) .
x9)) . in polynomial time.
in polynomial time. satisfiable exactly when the formula
satisfiable exactly when the formula  is satisfiable? If C has a satisfying assignment, each wire of the circuit has a well-defined value, and the output of the circuit is 1. Therefore, the assignment of wire values to variables in
is satisfiable? If C has a satisfying assignment, each wire of the circuit has a well-defined value, and the output of the circuit is 1. Therefore, the assignment of wire values to variables in  makes each clause of
makes each clause of  evaluate to 1, and thus the conjunction of all evaluates to 1. Conversely, if there is an assignment that causes
evaluate to 1, and thus the conjunction of all evaluates to 1. Conversely, if there is an assignment that causes  to evaluate to 1, the circuit C is satisfiable by an analogous argument. Thus, we have shown that CIRCUIT-SAT
to evaluate to 1, the circuit C is satisfiable by an analogous argument. Thus, we have shown that CIRCUIT-SAT  p SAT, which completes the proof.
p SAT, which completes the proof. 3-CNF satisfiability
(x1

 x1
x1 
 x2)
x2)  (x3
(x3  x2
x2  x4)
x4)  (
( x1
x1 
 x3
x3 
 x4)
x4)
 x1
x1 
 x2 ), which contains the three literals x1,
x2 ), which contains the three literals x1,  x1, and
x1, and  x2.
x2. in 3-CNF is satisfiable. The following theorem shows that a polynomial-time algorithm that can determine the satisfiability of boolean formulas is unlikely to exist, even when they are expressed in this simple normal form.
in 3-CNF is satisfiable. The following theorem shows that a polynomial-time algorithm that can determine the satisfiability of boolean formulas is unlikely to exist, even when they are expressed in this simple normal form. = ((x1
= ((x1  x2)
x2) 
 ((
(( x1
x1  x3)
x3)  x4))
x4)) 
 x2 .
x2 .
Figure 36.9 The tree corresponding to the formula
 NP applies equally well here to show that 3-CNF-SAT
NP applies equally well here to show that 3-CNF-SAT  NP. Thus, we need only show that 3-CNF-SAT is NP-hard. We prove this by showing that SAT
NP. Thus, we need only show that 3-CNF-SAT is NP-hard. We prove this by showing that SAT  p 3-CNF-SAT, from which the proof will follow by Lemma 36.8.
p 3-CNF-SAT, from which the proof will follow by Lemma 36.8. closer to the desired 3-conjunctive normal form.
closer to the desired 3-conjunctive normal form. p SAT in Theorem 36.9. First, we construct a binary "parse" tree for the input formula
p SAT in Theorem 36.9. First, we construct a binary "parse" tree for the input formula  , with literals as leaves and connectives as internal nodes. Figure 36.9 shows such a parse tree for the formula
, with literals as leaves and connectives as internal nodes. Figure 36.9 shows such a parse tree for the formula = ((x1
= ((x1  x2)
x2) 
 ((
(( x1
x1  x3)
x3)  x4))
x4)) 
 x2 .
x2 .(36.3)
 as the AND of the root variable and a conjunction of clauses describing the operation of each node. For the formula (36.3), the resulting expression is
as the AND of the root variable and a conjunction of clauses describing the operation of each node. For the formula (36.3), the resulting expression is ' = y1
' = y1  (y1
(y1  (y2
(y2 
 x2))
x2)) (y2
(y2  (y3
(y3  y4))
y4)) (y3
(y3  (x1
(x1  x2))
x2)) (y4
(y4 
 y5)
y5) (y5
(y5  (y6
(y6  y4))
y4)) (y6
(y6  (
( x1
x1  x3)).
x3)). ' thus obtained is a conjunction of clauses
' thus obtained is a conjunction of clauses  , each of which has at most 3 literals. The only additional requirement is that each clause be an OR of literals.
, each of which has at most 3 literals. The only additional requirement is that each clause be an OR of literals.y1 y2 x2 (y1
 (y2
(y2 
 x2))
x2))------------------------------
1 1 1 0
1 1 0 1
1 0 1 0
1 0 0 0
0 1 1 1
0 1 0 0
0 0 1 1
0 0 0 1
Figure 36.10 The truth table for the clause (y1
 (y2
(y2 
 x2)).
x2)). into conjunctive normal form. We construct a truth table for
into conjunctive normal form. We construct a truth table for  by evaluating all possible assignments to its variables. Each row of the truth table consists of a possible assignment of the variables of the clause, together with the value of the clause under that assignment. Using the truth-table entries that evaluate to 0, we build a formula in disjunctive normal form (or DNF)--an OR of AND's--that is equivalent to
by evaluating all possible assignments to its variables. Each row of the truth table consists of a possible assignment of the variables of the clause, together with the value of the clause under that assignment. Using the truth-table entries that evaluate to 0, we build a formula in disjunctive normal form (or DNF)--an OR of AND's--that is equivalent to  . We then convert this formula into a CNF formula
. We then convert this formula into a CNF formula  by using DeMorgan's laws (5.2) to complement all literals and change OR's into AND's and AND's into OR's.
by using DeMorgan's laws (5.2) to complement all literals and change OR's into AND's and AND's into OR's. into CNF as follows. The truth table for
into CNF as follows. The truth table for  'i is given in Figure 36.10. The DNF formula equivalent to
'i is given in Figure 36.10. The DNF formula equivalent to 
(y1
 y2
y2  x2)
x2)  (y1
(y1 
 y2
y2  x2)
x2)  (y1
(y1 
 y2
y2 
 x2)
x2)  (
( y1
y1  y2
y2 
 x2) .
x2) .
 .
. of the formula
of the formula  ' has now been converted into a CNF formula
' has now been converted into a CNF formula  , and thus
, and thus  ' is equivalent to the CNF formula
' is equivalent to the CNF formula  \" consisting of the conjunction of the
\" consisting of the conjunction of the  . Moreover, each clause of
. Moreover, each clause of  \" has at most 3 literals.
\" has at most 3 literals. ''' is constructed from the clauses of the CNF formula
''' is constructed from the clauses of the CNF formula  \". It also uses two auxiliary variables that we shall call p and q. For each clause Ci of
\". It also uses two auxiliary variables that we shall call p and q. For each clause Ci of  \", we include the following clauses in
\", we include the following clauses in  ''':
''': If Ci has 3 distinct literals, then simply include Ci as a clause of
If Ci has 3 distinct literals, then simply include Ci as a clause of  '''.
'''. If Ci has 2 distinct literals, that is, if Ci = (l1
If Ci has 2 distinct literals, that is, if Ci = (l1  l2), where l1 and l2 are literals, then include (l1
l2), where l1 and l2 are literals, then include (l1  l2
l2  p)
p)  (l1
(l1  l2
l2 
 p) as clauses of f(
p) as clauses of f( ). The literals p and
). The literals p and  p merely fulfill the syntactic requirement that there be exactly 3 distinct literals per clause: (l1
p merely fulfill the syntactic requirement that there be exactly 3 distinct literals per clause: (l1  l2
l2  p)
p)  (l1
(l1  l2
l2 
 p) is equivalent to (l1
p) is equivalent to (l1  l2) whether p = 0 or p = 1.
l2) whether p = 0 or p = 1. If Ci has just 1 distinct literal l, then include (l
If Ci has just 1 distinct literal l, then include (l  p
p  q)
q)  (l
(l  p
p 
 q)
q)  (l
(l 
 p
p  q)
q)  (l
(l 
 p
p 
 q) as clauses of
q) as clauses of  '''. Note that every setting of p and q causes the conjunction of these four clauses to evaluate to l.
'''. Note that every setting of p and q causes the conjunction of these four clauses to evaluate to l. ''' is satisfiable if and only if
''' is satisfiable if and only if  is satisfiable by inspecting each of the three steps. Like the reduction from CIRCUIT-SAT to SAT, the construction of
is satisfiable by inspecting each of the three steps. Like the reduction from CIRCUIT-SAT to SAT, the construction of  ' from
' from  in the first step preserves satisfiability. The second step produces a CNF formula
in the first step preserves satisfiability. The second step produces a CNF formula  \" that is algebraically equivalent to
\" that is algebraically equivalent to  '. The third step produces a 3-CNF formula
'. The third step produces a 3-CNF formula  ''' that is effectively equivalent to
''' that is effectively equivalent to  \", since any assignment to the variables p and q produces a formula that is algebraically equivalent to
\", since any assignment to the variables p and q produces a formula that is algebraically equivalent to  \".
\". ' from
' from  introduces at most 1 variable and 1 clause per connective in
introduces at most 1 variable and 1 clause per connective in  . Constructing
. Constructing  \" from
\" from  ' can introduce at most 8 clauses into
' can introduce at most 8 clauses into  \" for each clause from
\" for each clause from  ', since each clause of
', since each clause of  ' has at most 3 variables, and the truth table for each clause has at most 23 = 8 rows. The construction of
' has at most 3 variables, and the truth table for each clause has at most 23 = 8 rows. The construction of  ''' from
''' from  \" introduces at most 4 clauses into
\" introduces at most 4 clauses into  ''' for each clause of
''' for each clause of  \". Thus, the size of the resulting formula
\". Thus, the size of the resulting formula  ''' is polynomial in the length of the original formula. Each of the constructions can easily be accomplished in polynomial time.
''' is polynomial in the length of the original formula. Each of the constructions can easily be accomplished in polynomial time. Exercises
 P 3-CNF-SAT by using only the truth-table technique in the proof of Theorem 36.10, and not the other steps. That is, the professor proposes to take the boolean formula
P 3-CNF-SAT by using only the truth-table technique in the proof of Theorem 36.10, and not the other steps. That is, the professor proposes to take the boolean formula  , form a truth table for its variables, derive from the truth table a formula in 3-DNF that is equivalent to
, form a truth table for its variables, derive from the truth table a formula in 3-DNF that is equivalent to 
 , and then negate and apply DeMorgan's laws to produce a 3-CNF formula equivalent to
, and then negate and apply DeMorgan's laws to produce a 3-CNF formula equivalent to  . Show that this strategy does not yield a polynomial-time reduction.
. Show that this strategy does not yield a polynomial-time reduction. P. Make your algorithm as efficient as possible. (Hint: Observe that x
P. Make your algorithm as efficient as possible. (Hint: Observe that x  y is equivalent to
y is equivalent to  x
x  y. Reduce 2-CNF-SAT to a problem on a directed graph that is efficiently solvable.)
y. Reduce 2-CNF-SAT to a problem on a directed graph that is efficiently solvable.)36.5 NP-complete problems

Figure 36.11 The structure of NP-completeness proofs in Sections 36.4 and 36.5. All proofs ultimately follow by reduction from the NP-completeness of CIRCUIT-SAT.
36.5.1 The clique problem
 V of vertices, each pair of which is connected by an edge in E. In other words, a clique is a complete subgraph of G. The size of a clique is the number of vertices it contains. The clique problem is the optimization problem of finding a clique of maximum size in a graph. As a decision problem, we ask simply whether a clique of a given size k exists in the graph. The formal definition is
V of vertices, each pair of which is connected by an edge in E. In other words, a clique is a complete subgraph of G. The size of a clique is the number of vertices it contains. The clique problem is the optimization problem of finding a clique of maximum size in a graph. As a decision problem, we ask simply whether a clique of a given size k exists in the graph. The formal definition isCLIQUE = {
 G,k
G,k : G is a graph with a clique of size k}.
: G is a graph with a clique of size k}. , which is polynomial if k is a constant. In general, however, k could be proportional to |V|, in which case the algorithm runs in superpolynomial time. As one might suspect, an efficient algorithm for the clique problem is unlikely to exist.
, which is polynomial if k is a constant. In general, however, k could be proportional to |V|, in which case the algorithm runs in superpolynomial time. As one might suspect, an efficient algorithm for the clique problem is unlikely to exist. NP, for a given graph G = (V, E), we use the set V'
NP, for a given graph G = (V, E), we use the set V'  V of vertices in the clique as a certificate for G. Checking whether V' is a clique can be accomplished in polynomial time by checking whether, for every pair u, v
V of vertices in the clique as a certificate for G. Checking whether V' is a clique can be accomplished in polynomial time by checking whether, for every pair u, v  V', the edge (u, v) belongs to E.
V', the edge (u, v) belongs to E. p CLIQUE. That we should be able to prove this result is somewhat surprising, since on the surface logical formulas seem to have little to do with graphs.
p CLIQUE. That we should be able to prove this result is somewhat surprising, since on the surface logical formulas seem to have little to do with graphs.
Figure 36.12 The graph G derived from the 3-CNF formula
 = C1
= C1  C2
C2  C3, where C1 = (x1
C3, where C1 = (x1 
 x2
x2 
 x3), C2 =(
x3), C2 =( x1
x1  x2
x2  x3), and C3 = (x1
x3), and C3 = (x1  x2
x2  x3), in reducing 3-CNF-SAT to CLIQUE. A satisfying assignment of the formula is
x3), in reducing 3-CNF-SAT to CLIQUE. A satisfying assignment of the formula is  x1 = 0, x2 = 0, x3 = 1
x1 = 0, x2 = 0, x3 = 1 . This satisfying assignment satisfies C1 with
. This satisfying assignment satisfies C1 with  x2, and it satisfies C2 and C3 with x3, corresponding to the clique with lightly shaded vertices.
x2, and it satisfies C2 and C3 with x3, corresponding to the clique with lightly shaded vertices. = C1
= C1  C2
C2  . . .
. . .  Ck be a boolean formula in 3-CNF with k clauses. For r = 1, 2, . . . , k, each clause Cr has exactly three distinct literals
Ck be a boolean formula in 3-CNF with k clauses. For r = 1, 2, . . . , k, each clause Cr has exactly three distinct literals  . We shall construct a graph G such that
. We shall construct a graph G such that  is satisfiable if and only if G has a clique of size k.
is satisfiable if and only if G has a clique of size k. in
in  , we place a triple of vertices
, we place a triple of vertices  in V. We put an edge between two vertices
in V. We put an edge between two vertices  if both of the following hold:
if both of the following hold: 
 are in different triples, that is, r
are in different triples, that is, r  s, and
s, and their corresponding literals are consistent, that is,
their corresponding literals are consistent, that is,  is not the negation of
is not the negation of  .
. in polynomial time. As an example of this construction, if we have
in polynomial time. As an example of this construction, if we have = (x1
= (x1 
 x2
x2 
 x3)
x3)  (
( x1
x1  x2
x2  x3)
x3)  (x1
(x1  x2
x2  x3) ,
x3) , into G is a reduction. First, suppose that
into G is a reduction. First, suppose that  has a satisfying assignment. Then, each clause Cr contains at least one literal
has a satisfying assignment. Then, each clause Cr contains at least one literal  that is assigned 1, and each such literal corresponds to a vertex
that is assigned 1, and each such literal corresponds to a vertex  . Picking one such "true" literal from each clause yields a set of V' of k vertices. We claim that V' is a clique. For any two vertices
. Picking one such "true" literal from each clause yields a set of V' of k vertices. We claim that V' is a clique. For any two vertices  , where r
, where r  s, both corresponding literals
s, both corresponding literals  are mapped to 1 by the given satisfying assignment, and thus the literals cannot be complements. Thus, by the construction of G, the edge
are mapped to 1 by the given satisfying assignment, and thus the literals cannot be complements. Thus, by the construction of G, the edge  belongs to E.
belongs to E.
Figure 36.13 Reducing CLIQUE to VERTEX-COVER. (a) An undirected graph G = (V,E) with clique V' = {u,v,x,y}. (b) The graph
 produced by the reduction algorithm that has vertex cover V - V' = {w,z}.
produced by the reduction algorithm that has vertex cover V - V' = {w,z}. such that
such that  without fear of assigning 1 to both a literal and its complement, since G contains no edges between inconsistent literals. Each clause is satisfied, and so
without fear of assigning 1 to both a literal and its complement, since G contains no edges between inconsistent literals. Each clause is satisfied, and so  satisfied. (Any variables that correspond to no vertex in the clique may be set arbitrarily.)
satisfied. (Any variables that correspond to no vertex in the clique may be set arbitrarily.)  is
is  x1 = 0, x2 = 0, x3 = 1
x1 = 0, x2 = 0, x3 = 1 . A corresponding clique of size k = 3 consists of the vertices corresponding to
. A corresponding clique of size k = 3 consists of the vertices corresponding to  x2 from the first clause, x3 from the second clause, and x3 from the third clause.
x2 from the first clause, x3 from the second clause, and x3 from the third clause.36.5.2 The vertex-cover problem
 Vsuch that if (u, v)
Vsuch that if (u, v)  E, then u
E, then u  V' or v
V' or v  V' (or both). That is, each vertex "covers" its incident edges, and a vertex cover for G is a set of vertices that covers all the edges in E. The size of a vertex cover is the number of vertices in it. For example, the graph in Figure 36.13(b) has a vertex cover {w, z} of size 2.
V' (or both). That is, each vertex "covers" its incident edges, and a vertex cover for G is a set of vertices that covers all the edges in E. The size of a vertex cover is the number of vertices in it. For example, the graph in Figure 36.13(b) has a vertex cover {w, z} of size 2.VERTEX-COVER = {
 G, k
G, k : graph G has vertex cover of size k} .
: graph G has vertex cover of size k} . NP. Suppose we are given a graph G = (V, E) and an integer k. The certificate we choose is the vertex cover V'
NP. Suppose we are given a graph G = (V, E) and an integer k. The certificate we choose is the vertex cover V'  V itself. The verification algorithm affirms that |V'| = k, and then it checks, for each edge (u, v)
V itself. The verification algorithm affirms that |V'| = k, and then it checks, for each edge (u, v)  E, whether u
E, whether u  V' or v
V' or v  V'. This verification can be performed straightforwardly in polynomial time.
V'. This verification can be performed straightforwardly in polynomial time. P VERTEX-COVER. This reduction is based on the notion of the "complement" of a graph. Given an undirected graph G = (V, E), we define the complement of G as
P VERTEX-COVER. This reduction is based on the notion of the "complement" of a graph. Given an undirected graph G = (V, E), we define the complement of G as  . In other words,
. In other words,  is the graph containing exactly those edges that are not in G. Figure 36.13 shows a graph and its complement and illustrates the reduction from CLIQUE to VERTEX-COVER.
is the graph containing exactly those edges that are not in G. Figure 36.13 shows a graph and its complement and illustrates the reduction from CLIQUE to VERTEX-COVER. G, k
G, k of the clique problem. It computes the complement
of the clique problem. It computes the complement  , which is easily doable in polynomial time. The output of the reduction algorithm is the instance
, which is easily doable in polynomial time. The output of the reduction algorithm is the instance  , of the vertex-cover problem. To complete the proof, we show that this transformation is indeed a reduction: the graph G has a clique of size k if and only if the graph
, of the vertex-cover problem. To complete the proof, we show that this transformation is indeed a reduction: the graph G has a clique of size k if and only if the graph  has a vertex cover of size |V| - k.
has a vertex cover of size |V| - k. V with |V'| = k. We claim that V - V' is a vertex cover in
V with |V'| = k. We claim that V - V' is a vertex cover in  . Let (u, v) be any edge in
. Let (u, v) be any edge in  . Then, (u, v)
. Then, (u, v)  E, which implies that at least one of u or v does not belong to V', since every pair of vertices in V' is connected by an edge of E. Equivalently, at least one of u or v is in V - V', which means that edge (u,v) is covered by V - V'. Since (u, v) was chosen arbitrarily from
E, which implies that at least one of u or v does not belong to V', since every pair of vertices in V' is connected by an edge of E. Equivalently, at least one of u or v is in V - V', which means that edge (u,v) is covered by V - V'. Since (u, v) was chosen arbitrarily from  , every edge of
, every edge of  is covered by a vertex in V - V'. Hence, the set V - V', which has size |V| - k, forms a vertex cover for
is covered by a vertex in V - V'. Hence, the set V - V', which has size |V| - k, forms a vertex cover for  .
. has a vertex cover V'
has a vertex cover V'  V , where |V'| = |V| - k. Then, for all u, v
V , where |V'| = |V| - k. Then, for all u, v  V, if (u, v)
V, if (u, v)  , if
, if  , then u
, then u  V' or v
V' or v  V' or both. The contrapositive of this implication is that for all u, v
V' or both. The contrapositive of this implication is that for all u, v  V, if u
V, if u  V' and v
V' and v  V', then (u, v)
V', then (u, v)  E. In other words, V - V' is a clique, and it has size |V| - |V'| = k.
E. In other words, V - V' is a clique, and it has size |V| - |V'| = k. 36.5.3 The subset-sum problem
 N and a target t
N and a target t  N. We ask whether there is a subset S'
N. We ask whether there is a subset S'  S whose elements sum to t. For example, if S = {1, 4, 16, 64, 256, 1040, 1041, 1093, 1284, 1344} and t = 3754, then the subset S' = {1, 16, 64, 256, 1040, 1093, 1284} is a solution.
S whose elements sum to t. For example, if S = {1, 4, 16, 64, 256, 1040, 1041, 1093, 1284, 1344} and t = 3754, then the subset S' = {1, 16, 64, 256, 1040, 1093, 1284} is a solution.SUBSET-SUM =
{ S, t
S, t : there exists a subset S'
: there exists a subset S'  S such that t =
S such that t =  s
s S'S} .
S'S} . S, t
S, t of the problem, we let the subset S' be the certificate. Checking whether t =
of the problem, we let the subset S' be the certificate. Checking whether t =  s
s S's can be accomplished by a verification algorithm in polynomial time.
S's can be accomplished by a verification algorithm in polynomial time. P SUBSET-SUM. Given an instance
P SUBSET-SUM. Given an instance  G, k
G, k of the vertex-cover problem, the reduction algorithm constructs an instance
of the vertex-cover problem, the reduction algorithm constructs an instance  S, t
S, t of the subset-sum problem such that G has a vertex cover of size k if and only if there is a subset of S whose sum is exactly t.
of the subset-sum problem such that G has a vertex cover of size k if and only if there is a subset of S whose sum is exactly t. |E| matrix B = (bij) such that
|E| matrix B = (bij) such that

Figure 36.14 The reduction of the vertex-cover problem to the subset-sum problem. (a) An undirected graph G. A vertex cover {v1, v3, v4} of size 3 is lightly shaded. (b) The corresponding incidence matrix. Shading of the rows corresponds to the vertex cover of part (a). Each edge ej has a 1 in at least one lightly shaded row. (c) The corresponding subset-sum instance. The portion within the box is the incidence matrix. Here, the vertex cover {v1, v3, v4} of size k = 3 corresponds to the lightly shaded subset {1, 16, 64, 256, 1040, 1093, 1284}, which adds up to 3754.
 V, we create a positive integer xi whose modified base-4 representation consists of a leading 1 followed by |E| digits. The digits correspond to vi's row of the incidence matrix B = (bij) for G, as illustrated in Figure 36.14(c). Formally, for i = 0, 1, . . . , |V| - 1,
V, we create a positive integer xi whose modified base-4 representation consists of a leading 1 followed by |E| digits. The digits correspond to vi's row of the incidence matrix B = (bij) for G, as illustrated in Figure 36.14(c). Formally, for i = 0, 1, . . . , |V| - 1,
 E, we create a positive integer yj that is just a row of the "identity" incidence matrix. (The identity incidence matrix is the |E|
E, we create a positive integer yj that is just a row of the "identity" incidence matrix. (The identity incidence matrix is the |E|  |E| matrix with 1's only in the diagonal positions.) Formally, for j = 0, 1, . . . , |E| - 1,
|E| matrix with 1's only in the diagonal positions.) Formally, for j = 0, 1, . . . , |E| - 1,yj = 4j .

 S whose sum is t. First, suppose that G has a vertex cover V'
S whose sum is t. First, suppose that G has a vertex cover V'  V of size k. Let V' = {vi1, vi2, . . . , vik}, and define S' by
V of size k. Let V' = {vi1, vi2, . . . , vik}, and define S' byS' = {xi1, xi2, . . . , xik} 
{yj : ej is incident on precisely one vertex in V'} . s
s S'S = t, observe that summing the k leading 1's of the xim
S'S = t, observe that summing the k leading 1's of the xim  S' gives the leading digit k of the modified base-4 representation of t. To get the low-order digits of t, each of which is a 2, consider the digit positions in turn, each of which corresponds to an edge ej. Because V' is a vertex cover, ej is incident on at least one vertex in V'. Thus, for each edge ej, there is at least one xim
S' gives the leading digit k of the modified base-4 representation of t. To get the low-order digits of t, each of which is a 2, consider the digit positions in turn, each of which corresponds to an edge ej. Because V' is a vertex cover, ej is incident on at least one vertex in V'. Thus, for each edge ej, there is at least one xim  S' with a 1 in the jth position. If ej is incident on two vertices in V', then both contribute a 1 to the sum in the jth position. The jth digit of yj contributes nothing, since ej is incident on two vertices, which implies that yj
S' with a 1 in the jth position. If ej is incident on two vertices in V', then both contribute a 1 to the sum in the jth position. The jth digit of yj contributes nothing, since ej is incident on two vertices, which implies that yj  S'. Thus, in this case, the sum of S' produces a 2 in the jth position of t. For the other case--when ej is incident on exactly one vertex in V'--we have yj
S'. Thus, in this case, the sum of S' produces a 2 in the jth position of t. For the other case--when ej is incident on exactly one vertex in V'--we have yj  S', and the incident vertex and yj each contribute 1 to the sum of the jth digit of t, thereby also producing a 2. Thus, S' is a solution to the subset-sum instance S.
S', and the incident vertex and yj each contribute 1 to the sum of the jth digit of t, thereby also producing a 2. Thus, S' is a solution to the subset-sum instance S. S that sums to t. Let S = {xi1, xi2, . . . , xim}
S that sums to t. Let S = {xi1, xi2, . . . , xim}  {yj1, yj2, . . . , yjp}. We claim that m = k and that V' = {vi1, vi2, . . . , vim} is a vertex cover for G. To prove this claim, we start by observing that for each edge ej
{yj1, yj2, . . . , yjp}. We claim that m = k and that V' = {vi1, vi2, . . . , vim} is a vertex cover for G. To prove this claim, we start by observing that for each edge ej  E, there are three 1's in set S in the ej position: one from each of the two vertices incident on ej, and one from yj. Because we are working with a modified base-4 representation, there are no carries from position ej to position ej+1. Thus, for each of the |E| low-order positions of t, at least one and at most two xi must contribute to the sum. Since at least one xi contributes to the sum for each edge, we see that V' is a vertex cover. To see that m = k, and thus that V' is a vertex cover of size k, observe that the only way the leading k in target t can be achieved is by including exactly k of the xi in the sum.
E, there are three 1's in set S in the ej position: one from each of the two vertices incident on ej, and one from yj. Because we are working with a modified base-4 representation, there are no carries from position ej to position ej+1. Thus, for each of the |E| low-order positions of t, at least one and at most two xi must contribute to the sum. Since at least one xi contributes to the sum for each edge, we see that V' is a vertex cover. To see that m = k, and thus that V' is a vertex cover of size k, observe that the only way the leading k in target t can be achieved is by including exactly k of the xi in the sum. 36.5.4 The hamiltonian-cycle problem

Figure 36.15 (a) Widget A, used in the reduction from 3-CNF-SAT to HAM-CYCLE. (b)-(c) If A is a subgraph of some graph G that contains a hamiltonian cycle and the only connections from A to the rest of G are through the vertices a, a', b, and b', then the shaded edges represent the only two possible ways in which the hamiltonian cycle may traverse the edges of subgraph A. (d) A compact representation of the A widget.
 P HAM-CYCLE. Given a 3-CNF boolean formula
P HAM-CYCLE. Given a 3-CNF boolean formula  over variables x1, x2, . . . , xn with clauses C1, C2, . . . , Ck, each containing exactly 3 distinct literals, we construct a graph G = (V, E) in polynomial time such that G has a hamiltonian cycle if and only if
over variables x1, x2, . . . , xn with clauses C1, C2, . . . , Ck, each containing exactly 3 distinct literals, we construct a graph G = (V, E) in polynomial time such that G has a hamiltonian cycle if and only if  is satisfiable. Our construction is based on widgets, which are pieces of graphs that enforce certain properties.
is satisfiable. Our construction is based on widgets, which are pieces of graphs that enforce certain properties. , we include a copy of widget B, and we join these widgets together in series as follows. Letting bij be the copy of vertex bj in the ith copy of widget B, we connect bi,4 to bi+1,1 for i = 1, 2, . . . , k - 1.
, we include a copy of widget B, and we join these widgets together in series as follows. Letting bij be the copy of vertex bj in the ith copy of widget B, we connect bi,4 to bi+1,1 for i = 1, 2, . . . , k - 1. , we include two vertices
, we include two vertices  . We connect these two vertices by means of two copies of the edge
. We connect these two vertices by means of two copies of the edge  , which we denote by em and
, which we denote by em and  to distinguish them. The idea is that if the hamiltonian cycle takes edge em, it corresponds to assigning variable xm the value 1. If the hamiltonian cycle takes edge
to distinguish them. The idea is that if the hamiltonian cycle takes edge em, it corresponds to assigning variable xm the value 1. If the hamiltonian cycle takes edge  , the variable is assigned the value 0. Each pair of these edges forms a two-edge loop; we connect these small loops in series by adding edges
, the variable is assigned the value 0. Each pair of these edges forms a two-edge loop; we connect these small loops in series by adding edges  for m = 1, 2, . . . , n - 1. We connect the left (clause) side of the graph to the right (variable) side by means of two edges
for m = 1, 2, . . . , n - 1. We connect the left (clause) side of the graph to the right (variable) side by means of two edges  , which are the topmost and bottommost edges in Figure 36.17.
, which are the topmost and bottommost edges in Figure 36.17. xm, then we instead put an A widget between edge (bij, bi,j+1) and edge
xm, then we instead put an A widget between edge (bij, bi,j+1) and edge  . In Figure 36.17, for example, because clause C2 is (x1
. In Figure 36.17, for example, because clause C2 is (x1 
 x2
x2  x3), we place three A widgets as follows:
x3), we place three A widgets as follows: between (b2,1, b2,2) and e1,
between (b2,1, b2,2) and e1, between (b2,2, b2,3) and
between (b2,2, b2,3) and  , and
, and between (b2,3, b2,4) and e3.
between (b2,3, b2,4) and e3. xm in Figure 36.17, for example), and thus an edge em or
xm in Figure 36.17, for example), and thus an edge em or  may be be influenced by several A widgets (edge
may be be influenced by several A widgets (edge  , for example). In this case, we connect the A widgets in series, as shown in Figure 36.18, effectively replacing edge em or
, for example). In this case, we connect the A widgets in series, as shown in Figure 36.18, effectively replacing edge em or  by a series of edges.
by a series of edges.
Figure 36.16 Widget B, used in the reduction from 3-CNF-SAT to HAM-CYCLE. No path from vertex b1 to vertex b4 containing all the vertices in the widget may use all three edges (b1, b2), (b2, b3), and (b3, b4). Any proper subset of these edges may be used, however. (a)-(e) Five such subsets. (f) A representation of this widget in which at least one of the paths pointed to by the arrows must be taken by a hamiltonian cycle.

Figure 36.17 The graph G constructed from the formula
 = (
= ( x1 V x2 V
x1 V x2 V  x3)
x3)  (x1 V
(x1 V  x2 V x3)
x2 V x3)  (x1 V x2 V
(x1 V x2 V  x3). A satisfying assignment s to the variables of
x3). A satisfying assignment s to the variables of  is s(x1) = 0, s(x2) = 1, and s(x3) = 1, which corresponds to the hamiltonian cycle shown. Note that if s(xm) = 1, then edge em is in the hamiltonian cycle, and if s(xm) = 0, then edge
is s(x1) = 0, s(x2) = 1, and s(x3) = 1, which corresponds to the hamiltonian cycle shown. Note that if s(xm) = 1, then edge em is in the hamiltonian cycle, and if s(xm) = 0, then edge  is in the hamiltonian cycle.
is in the hamiltonian cycle.
Figure 36.18 The actual construction used when an edge em or
 is influenced by multiple A widgets. (a) A portion of Figure 36.17. (b) The actual subgraph constructed.
is influenced by multiple A widgets. (a) A portion of Figure 36.17. (b) The actual subgraph constructed. is satisfiable if and only if graph G contains a hamiltonian cycle. We first suppose that G has a hamiltonian cycle h and show that
is satisfiable if and only if graph G contains a hamiltonian cycle. We first suppose that G has a hamiltonian cycle h and show that  is satisfiable. Cycle h must take a particular form:
is satisfiable. Cycle h must take a particular form: First, it traverses edge
First, it traverses edge  to go from the top left to the top right.
to go from the top left to the top right. It then follows all of the
It then follows all of the  vertices from top to bottom, choosing either edge em or edge
vertices from top to bottom, choosing either edge em or edge  , but not both.
, but not both. It next traverses edge
It next traverses edge  to get back to the left side.
to get back to the left side. Finally, it traverses the B widgets from bottom to top on the left.
Finally, it traverses the B widgets from bottom to top on the left. as follows. If edge em belongs to h, then we set xm = 1. Otherwise, edge
as follows. If edge em belongs to h, then we set xm = 1. Otherwise, edge  belongs to h, and we set xm = 0.
belongs to h, and we set xm = 0. . Consider a clause Ci and the corresponding B widget in G. Each edge (bi,jbi,j+l) is connected by an A widget to either edge em or edge
. Consider a clause Ci and the corresponding B widget in G. Each edge (bi,jbi,j+l) is connected by an A widget to either edge em or edge  , depending on whether xm or
, depending on whether xm or  xm is the jth literal in the clause. The edge (bi,j,bi,j+1) is traversed by h if and only if the corresponding literal is 0. Since each of the three edges (bi,1,bi,2),(bi,2,bi,3),(bi,3,bi,4) in clause Ci is also in a B widget, all three cannot be traversed by the hamiltonian cycle h. One of the three edges, therefore, must have a corresponding literal whose assigned value is 1, and clause Ci is satisfied. This property holds for each clause Ci, i = 1, 2, . . . , k, and thus formula ø is satisfied.
xm is the jth literal in the clause. The edge (bi,j,bi,j+1) is traversed by h if and only if the corresponding literal is 0. Since each of the three edges (bi,1,bi,2),(bi,2,bi,3),(bi,3,bi,4) in clause Ci is also in a B widget, all three cannot be traversed by the hamiltonian cycle h. One of the three edges, therefore, must have a corresponding literal whose assigned value is 1, and clause Ci is satisfied. This property holds for each clause Ci, i = 1, 2, . . . , k, and thus formula ø is satisfied.
Figure 36.19 An instance of the traveling-salesman problem. Shaded edges represent a minimum-cost tour, with cost 7.
 if xm = 0, and traverse edge (bi,j,bi,j+1) if and only if the jth literal of clause Ci is 0 under the assignment. These rules can indeed be followed, since we assume that s is a satisfying assignment for formula ø.
if xm = 0, and traverse edge (bi,j,bi,j+1) if and only if the jth literal of clause Ci is 0 under the assignment. These rules can indeed be followed, since we assume that s is a satisfying assignment for formula ø.36.5.5 The traveling-salesman problem
 u, w, v, x, u
u, w, v, x, u , with cost 7. The formal language for the traveling-salesman problem is
, with cost 7. The formal language for the traveling-salesman problem isTSP = {
 G,c,k
G,c,k : G = (V,E) is a complete graph,
: G = (V,E) is a complete graph,c is a function from V
 V
V  Z,
Z,k
 Z, and
Z, andG has a traveling-salesman tour with cost at most k} .
 p TSP. Let G = (V, E) be an instance of HAM-CYCLE. We construct an instance of TSP as follows. We form the complete graph G'= (V,E'), where E' = {(i, j): i, j
p TSP. Let G = (V, E) be an instance of HAM-CYCLE. We construct an instance of TSP as follows. We form the complete graph G'= (V,E'), where E' = {(i, j): i, j  V}, and we define the cost function c by
V}, and we define the cost function c by
Exercises
 b. Prove that 0-1 integer programming is NP-complete. (Hint: Reduce from 3-CNF-SAT.)
b. Prove that 0-1 integer programming is NP-complete. (Hint: Reduce from 3-CNF-SAT.) such that
such that  . Show that the set-partition problem is NP-complete.
. Show that the set-partition problem is NP-complete.Problems
 V of vertices such that each edge in E is incident on at most one vertex in V'. The independent-set problem is to find a maximum-size independent set in G.
V of vertices such that each edge in E is incident on at most one vertex in V'. The independent-set problem is to find a maximum-size independent set in G.
Figure 36.20 The widget corresponding to a clause (x V y V z), used in Problem 36-2.
 {1, 2, . . . , k} such that c(u)
{1, 2, . . . , k} such that c(u)  c(v) for every edge (u,v)
c(v) for every edge (u,v)  E. In other words, the numbers 1, 2, . . . , k represent the k colors, and adjacent vertices must have different colors. The graph-coloring problem is to determine the minimum number of colors needed to color a given graph.
E. In other words, the numbers 1, 2, . . . , k represent the k colors, and adjacent vertices must have different colors. The graph-coloring problem is to determine the minimum number of colors needed to color a given graph. xi, and RED for i = 1, 2, . . . , n.
xi, and RED for i = 1, 2, . . . , n.Chapter notes
 NP. The notion of NP-completeness was proposed in 1971 by Cook [49], who gave the first NP-completeness proofs for formula satisfiability and 3-CNF satisfiability. Levin [138] independently discovered the notion, giving an NP-completeness proof for a tiling problem. Karp [116] introduced the methodology of reductions in 1972 and demonstrated the rich variety of NP-complete problems. Karp's paper included the original NP-completeness proofs of the clique, vertex-cover, and hamiltonian-cycle problems. Since then, hundreds of problems have been proven to be NP-complete by many researchers.
NP. The notion of NP-completeness was proposed in 1971 by Cook [49], who gave the first NP-completeness proofs for formula satisfiability and 3-CNF satisfiability. Levin [138] independently discovered the notion, giving an NP-completeness proof for a tiling problem. Karp [116] introduced the methodology of reductions in 1972 and demonstrated the rich variety of NP-complete problems. Karp's paper included the original NP-completeness proofs of the clique, vertex-cover, and hamiltonian-cycle problems. Since then, hundreds of problems have been proven to be NP-complete by many researchers.


