Efficient Volumetric PolyCube-Map Construction
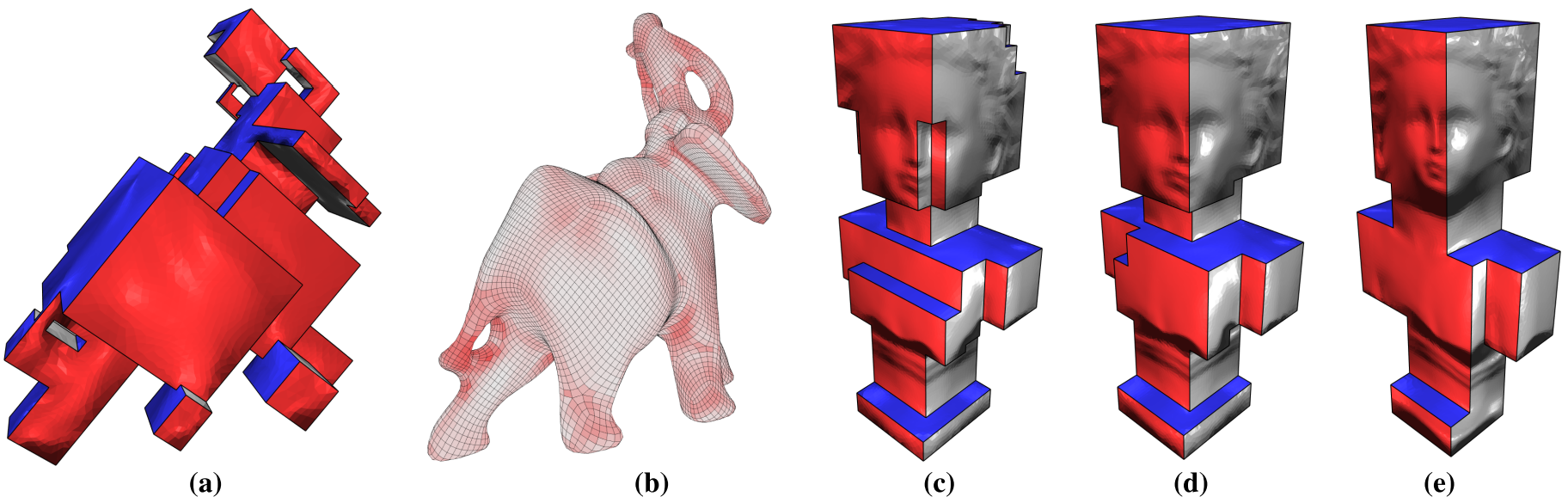
Figure 1:(a) The volumetric PolyCube-map for the Elephant model (48k tetrahedrons). Our method took 17 seconds to achieve the PolyCube-map whose maximum isomeric distortion is \(11.7\) and the number of corners is 176. (b) The all-hex meshing result from (a). The hexahedral mesh has 46994 hexes, and the minimal and average scaled Jacobian are 0.231 and 0.887. The hexes are color-coded by their scaled Jacobian values, with white being optimal. PolyCube-maps for the Buste model using different Gaussian smoothing kernel \(\sigma\) are shown in (c), (d) and (e). From (c) to (e), the results have 128 (\(\sigma = \bar{l}_e\) where \(\bar{l}_e\) is the average boundary edge length of the input mesh), 72 (\(\sigma = 1.5\,\bar{l}_e\)) and 36 (\(\sigma = 2\,\bar{l}_e\)) corners and the average isometric distortions are 1.50, 1.53 and 1.57, respectively.
Abstract
PolyCubes provide compact representations for closed complex shapes and are essential to many computer graphics applications. Existing automatic PolyCube construction methods usually suffer from poor quality or time-consuming computation. In this paper, we provide a highly efficient method to compute volumetric PolyCube-maps. Given an input tetrahedral mesh, we utilize two novel normal-driven volumetric deformation schemes and a polycube-allowable mesh segmentation to drive the input to a volumetric PolyCube structure. Our method can robustly generate foldover-free and low-distortion PolyCube-maps in practice, and provide a flexible control on the number of corners of Polycubes. Compared with state-of-the-art methods, our method is at least one order of magnitude faster and has better mapping qualities. We demonstrate the efficiency and efficacy of our method in PolyCube construction and all-hexahedral meshing on various complex models.
Downloads
Paper, All-Hex mesh data, PolyCube data set (Dropbox version), Slides, Part of the code.
Data Set containts 106 models which vary from natrual objects to CAD models. It is mainly based on the benchmark of global seamless parameterization and mesh segmentation.

Figure 2: Gallery of polycube maps of selected 23 models.
Summary
Our goal: Desing an PolyCube-map construction algorithm which satisfies the following properties: (1) the algorithm is automatic without or with minimal manual intervention; (2) the PolyCube-map is free of foldovers and degenerate elements; (3) the mapping distortion is as low as possible; (4) the complexity of the PolyCube, i.e. the number of corners, is controllable; (5) the algorithm should be efficient, otherwise manual construction is preferable.
The idea: Following figure illustrates the main workflow of our algorithm.
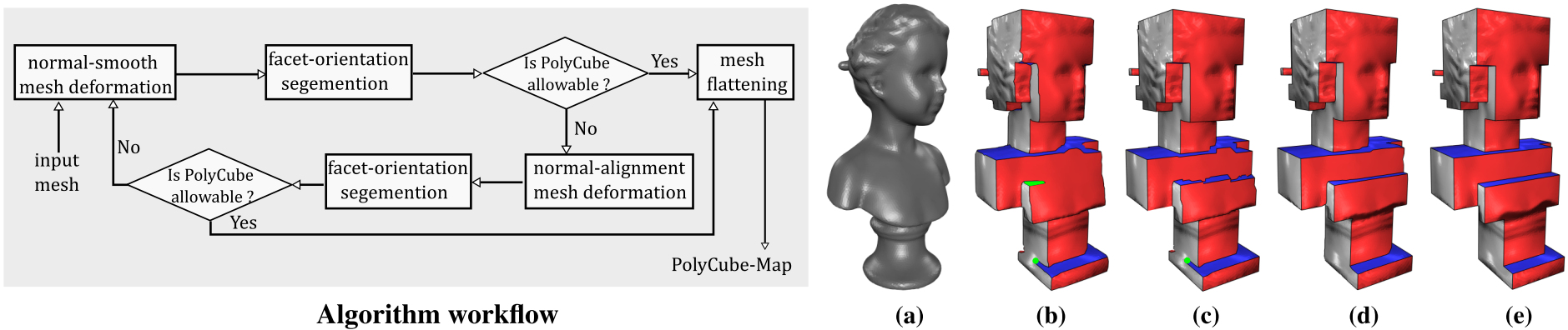
Figure 3: The left figure is our algorithm workflow. The right figure shows the results of each step of the algorithm applied to the Buste model. (a): The input tetrahedral mesh. (b): The result after the normal-smooth mesh deformation and mesh segmentation. Facets with the same label are with the same color. The segmentation result violates the sufficient topological conditions of the PolyCube structure. See the green chart that has only two neighboring charts. There is a turning point at the base (see the green circle). (c): The result after applying the normal-alignment deformation and mesh segmentation to (b). (d): The result after applying another round of the normal-smooth deformation and mesh segmentation to (c). The sufficient conditions of the PolyCube structure are satisfied and all the turning points are eliminated. (e): the final PolyCube-map after mesh flattening.
Application: All-Hex meshing.

Figure 4: Gallery of our polycube maps and all-hex meshing results.
Bibtex
@article {Fu-2016-PC,
title = {Efficient Volumetric PolyCube-Map Construction},
author = {Xiao-Ming Fu and Chong-Yang Bai and Yang Liu},
journal = {Computer Graphics Forum (Pacific Graphics)},
volume = {35},
number = {7},
year = {2016},
}