极限理论
复习
|
张瑞
中国科学技术大学数学科学学院
rui@ustc.edu.cn |
复习
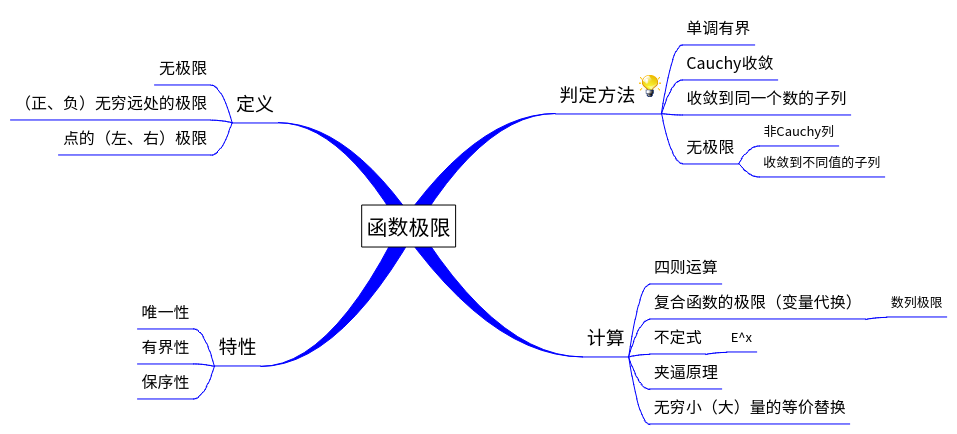
函数极限
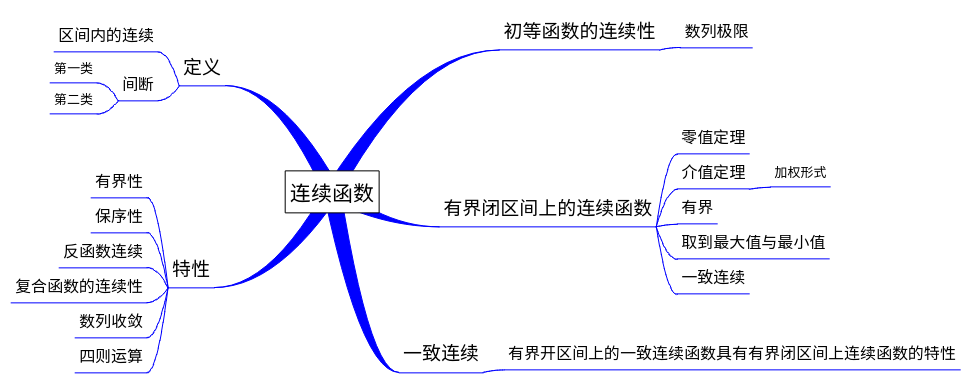
函数连续
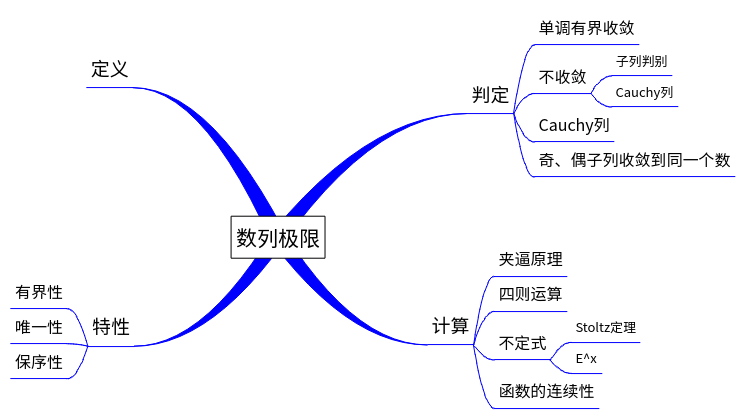
数列极限
习题
例 1. 求极限
其中是常数。
例 2. 求
例 3. 设。试证:若极限 存在,则有
例 4. 若
则
例 5. 求
例 6. 若
求,
例 7. 已知满足
则
例 8. 已知,且等号成立的充要条件是。 若正项数列满足
证明存在,并求这个极限。
例 9. 函数在上连续,, , , , 是上的一个点列,求
例 10. 若, ,则
例 11. 函数在上连续,且,证明:存在,满足
例 12. 函数在上连续,且,证明:存在,满足
例 13. 设, 均为上严格单调增的正的连续函数,证明:存在,满足
例 14. 设在上连续,且
证明,存在,使
例 15. 设,求的间断点。