坐标变换与其它常用坐标系

空间解析几何

张瑞
中国科学技术大学数学科学学院

坐标变换与其它常用坐标系

坐标变换

空间中，两个不同的右手直角坐标系，其中一个可以通过平移与旋转与另一个重合。

  • 设$F=[O;\vec i, \vec j, \vec k]$和$F'=[O';\vec i', \vec j', \vec k']$是 空间中两个不同的右手直角坐标系。
  • 点$P$在两个坐标系下的坐标分别是$(x,y,z)$和$(x',y',z')$。
  • 下面，来看两个坐标之间的关系。

平移

设$F$和$F'$的坐标系坐标轴方向相同，原点不同，即$O'\neq O$, $\vec i'=\vec i$, $\vec j'=\vec j$, $\vec k'=\vec k$。 且有

\[\overrightarrow{OP}=x\vec i+y\vec j+z\vec k, \quad \overrightarrow{O'P}=x'\vec i+y'\vec j+z'\vec k \]

注意到$\overrightarrow{O'P}=\overrightarrow{OP}-\overrightarrow{OO'}$，

  • 并设$\overrightarrow{OO'}=a\vec i+b\vec j+c\vec k$（即$O'$在坐标系$F$下的坐标是$(a,b,c)$，则有
    \[x'\vec i+y'\vec j+z'\vec k=(x-a)\vec i+(y-b)\vec j+(z-c)\vec k \]

    得到平移坐标变换公式

    \[x'=x-a, \quad y'=y-b, \quad z'=z-c \]

例 1. 下面方程刻画的是什么图形

\[4x^2+25y^2+4z^2-16x-50y-16z-43=0 \]

解. 配方，原方程变为

\[4(x-2)^2+25(y-1)^2+4(z-2)^2-100=0 \]

将坐标原点平移到$(2,1,2)$，即取

\[x'=x-2, y'=y-1, z'=z-2 \]

代入得到

\[\frac{x'^2}{5^2}+\frac{y'^2}{2^2}+\frac{z'^2}{5^2}=1 \]

是个（旋转）椭球面。

旋转

设两个右手直角坐标系$F$和$F'$的原点相同，但坐标轴方向不同。

\begin{tikzpicture} \draw[-latex] (0,0) node[left] {$O$} -- (0:2) node[below] {$\vec j$}; \draw[-latex] (0,0) -- (90:2) node[above] {$\vec k$}; \draw[-latex] (0,0) -- (-120:1) node[below] {$\vec i$}; \draw[-latex, blue] (0,0) -- (30:1.8) node[right] {$\vec j'$}; \draw[-latex, blue] (0,0) -- (120:1.8) node[above] {$\vec k'$}; \draw[-latex, blue] (0,0) -- (-100:0.8) node[below] {$\vec i'$}; \end{tikzpicture}
  • 设两个坐标系的基向量$\{\vec i, \vec j,\vec k\}$和$\{\vec i', \vec j',\vec k'\}$ 之间的夹角为
$\vec i$ $\vec j$ $\vec k$
$\vec i'$ $\alpha_1$ $\beta_1$ $\gamma_1$
$\vec j'$ $\alpha_2$ $\beta_2$ $\gamma_2$
$\vec k'$ $\alpha_3$ $\beta_3$ $\gamma_3$

利用方向余弦表示，知道

\[\begin{aligned} \vec i'=\cos(\alpha_1)\vec i+\cos(\beta_1)\vec j+\cos(\gamma_1)\vec k \\ \vec j'=\cos(\alpha_2)\vec i+\cos(\beta_2)\vec j+\cos(\gamma_2)\vec k \\ \vec k'=\cos(\alpha_3)\vec i+\cos(\beta_3)\vec j+\cos(\gamma_3)\vec k \\ \end{aligned} \]

又$\vec i'$, $\vec j'$, $\vec k'$两两正交，因此对$i,j=1,2,3$成立

\[\cos(\alpha_i)\cos(\alpha_j)+\cos(\beta_i)\cos(\beta_j) +\cos(\gamma_i)\cos(\gamma_j)=\delta_{ij} \]

点$P$在两个坐标系下的坐标分别是$(x,y,z)$和$(x',y',z')$，则有

\[\begin{aligned} \overrightarrow{OP}=&x\vec i+y\vec j+z\vec k \\ =&x'\vec i'+y'\vec j'+z'\vec k' \\ =&x'(\cos(\alpha_1)\vec i+\cos(\beta_1)\vec j+\cos(\gamma_1)\vec k) \\ & + y'(\cos(\alpha_2)\vec i+\cos(\beta_2)\vec j+\cos(\gamma_2)\vec k) \\ & + z'(\cos(\alpha_3)\vec i+\cos(\beta_3)\vec j+\cos(\gamma_3)\vec k) \\ =&(x'\cos(\alpha_1)+y'\cos(\alpha_2)+z'\cos(\alpha_3))\vec i \\ &+(x'\cos(\beta_1)+y'\cos(\beta_2)+z'\cos(\beta_3))\vec j \\ &+(x'\cos(\gamma_1)+y'\cos(\gamma_2)+z'\cos(\gamma_3))\vec k \\ \end{aligned} \]

由线性代数的知识，存在正交阵$A=(a_{ij})$，成立

\[\begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} =A \begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} \]

若点$P$在两个坐标系下的坐标分别是$(x,y,z)$和$(x',y',z')$，则有

\[\begin{aligned} \overrightarrow{OP}=&\begin{pmatrix} x & y & z\end{pmatrix}\begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} =\begin{pmatrix} x' & y' & z'\end{pmatrix}\begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} \\ =&\begin{pmatrix} x' & y' & z'\end{pmatrix}A \begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} \end{aligned} \]

得到旋转坐标变换公式：

\[\begin{aligned} x= & x'\cos(\alpha_1)+y'\cos(\alpha_2)+z'\cos(\alpha_3) \\ y= & x'\cos(\beta_1)+y'\cos(\beta_2)+z'\cos(\beta_3) \\ z= & x'\cos(\gamma_1)+y'\cos(\gamma_2)+z'\cos(\gamma_3) \\ \end{aligned} \]

同样，有

\[\begin{aligned} x'= & x\cos(\alpha_1)+y\cos(\beta_1)+z\cos(\gamma_1) \\ y'= & x\cos(\alpha_2)+y\cos(\beta_2)+z\cos(\gamma_2) \\ z'= & x\cos(\alpha_3)+y\cos(\beta_3)+z\cos(\gamma_3) \\ \end{aligned} \]

由$A$正交，因此

\[\begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} =A^{T} \begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} \]

则有

\[\begin{aligned} \overrightarrow{OP}=&\begin{pmatrix} x & y & z\end{pmatrix}\begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} =\begin{pmatrix} x' & y' & z'\end{pmatrix}\begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} \\ =&\begin{pmatrix} x & y & z\end{pmatrix}A^T \begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} \end{aligned} \]

当一个轴不动时（如$z$轴不动），则有

绕$z$轴逆时针旋转后

$\vec i$ $\vec j$ $\vec k$
$\vec i'$ $\alpha$ $\frac{\pi}2-\alpha$ $\frac{\pi}2$
$\vec j'$ $\frac{\pi}2+\alpha$ $\alpha$ $\frac{\pi}2$
$\vec k'$ $\frac{\pi}2$ $\frac{\pi}2$ $0$

坐标转换公式为

\[\begin{aligned} x=&x'\cos(\alpha)-y'\sin(\alpha) \\ y=&x'\sin(\alpha)+y'\cos(\alpha) \\ z=&z' \end{aligned} \]

绕$z$轴顺时针旋转后

$\vec i$ $\vec j$ $\vec k$
$\vec i'$ $\alpha$ $\frac{\pi}2+\alpha$ $\frac{\pi}2$
$\vec j'$ $\frac{\pi}2-\alpha$ $\alpha$ $\frac{\pi}2$
$\vec k'$ $\frac{\pi}2$ $\frac{\pi}2$ $0$

坐标转换公式为

\[\begin{aligned} x=&x'\cos(\alpha)+y'\sin(\alpha) \\ y=&-x'\sin(\alpha)+y'\cos(\alpha) \\ z=&z' \end{aligned} \]

例 2. 将直角坐标系$Oxyz$绕$z$轴逆时针旋转$\frac{\pi}4$后，得到新坐标系$Ox'y'z'$。 试表示新旧坐标间的变换关系，并给出方程$xy=z$在新坐标系下的表达式

解. 依题意，有

\[\begin{aligned} x=&x'\cos(\frac{\pi}4)-y'\sin(\frac{\pi}4)=\frac{\sqrt 2}2(x'-y') \\ y=&x'\sin(\frac{\pi}4)+y'\cos(\frac{\pi}4)=\frac{\sqrt 2}2(x'+y') \\ z=&z' \end{aligned} \]

代入方程后，得到 $\frac{\sqrt 2}2(x'-y')\frac{\sqrt 2}2(x'+y')=z'$，

即有 $\displaystyle\frac{x'^2}2-\frac{y'^2}2=z'$ 是一个马鞍面。

注意到标准二次曲面方程中，不含$xy$, $yz$, $xz$等项，需要在新坐标下的表达式中去掉这类项。令$a^2+b^2=1$，且

\[\begin{cases} x=a x' - b y' \\ y=b x' + a y' \\ z=z' \\ \end{cases} \]

代入方程$xy=z$，有

\[ab x'^2+(a^2-b^2)x'y'-aby'^2=z' \]

取$a=b=\sqrt{\frac12}$，则有

\[\frac12 x'^2-\frac12 y'^2=z' \]

例 3. 利用坐标变换化简方程

\[45x^2+45y^2-8z^2-54xy +36\sqrt 2 x-108\sqrt2 y+32z+184=0 \]

并指出它是什么曲面。

解. 注意到标准二次曲面方程中，不含$xy$, $yz$, $xz$等项，需要在新坐标下的表达式中去掉这类项。

令$a^2+b^2=1$，且

\[\begin{cases} x=a x' - b y' \\ y=b x' + a y' \\ z=z' \\ \end{cases} \]

则$45x^2+45y^2-54xy$变成

\[\begin{aligned} 45x^2+45y^2-54xy =&45(a^2x'^2+b^2y'^2-2abx'y') \\ &+45(b^2x'^2+a^2y'^2+2abx'y') \\ &-54(ab x'^2+(a^2-b^2)x'y'-aby'^2) \end{aligned} \]

取合适的$a$, $b$，使

\[45(2ab-2ab)-54(a^2-b^2)=0 \]

即$a=b=\sqrt{\frac12}$，坐标变换公式为

\[\begin{cases} x=\frac1{\sqrt 2}( x' - y') \\ y=\frac1{\sqrt 2}( x' + y') \\ z=z' \\ \end{cases} \]

代入后，有

\[9x'^2+36y'^2-4z'^2-36x'-72y'+16z'+92=0 \]

配方

\[9(x'-2)^2+36(y'-1)^2-4(z'-2)^2+36=0 \]

坐标平移

\[x'' = x'-2, y'' = y'-1, z'' = z'-2 \]

是一个双叶双曲面。

对于更一般的表达式

\[A x^2+B y^2+C z^2+D xy+Eyz+Fxz \]

令 $\displaystyle\begin{cases}x=a_{11} x' + a_{12} y' + a_{13} z' \\y=a_{21} x' + a_{22} y' + a_{23} z' \\z=a_{31} x' + a_{32} y' + a_{33} z' \\\end{cases}$， 则系数$a_{ij}$满足:

  1. 如下6个表达式

    \[\begin{aligned} a_{i1}a_{j1}+a_{i1}a_{j2}+a_{i3}a_{j3}=\delta_{ij}, i=1,2,3, j=1,2,3 \\ \end{aligned} \]

  2. 如下3个表达式。

    代入后，得到$x'y'$, $y'z'$, $z'x'$的系数为$0$。

更好的方法，在线性代数课程中介绍。

其它常用坐标系

前面介绍的坐标系，是由一个原点和三个不共面的向量组成。这样的空间坐标系是线性坐标系， 它的一个坐标分量等于常量所对应的面都是平面。

下面介绍一些常见的非线性坐标系。

平面的极坐标系

定义 1.
平面上的极坐标系可以按如下方法构造，

  • 在平面上取定一点$O$(称为极点),
  • 从极点引一条射线$Ox$(称为极轴)，
  • 再选定一个长度单位和角度的正向(通常取逆时针方向为正)

这样就构成的平面上的极坐标系。

对于平面上任意一点$P$，

  • 用$r$表示$P$到$O$的距离(向量$\overrightarrow{OP}$的长度)，$r$的取值范围是$[0,+\infty)$
  • $\theta$表示从极轴到向量$\overrightarrow{OP}$的正向夹角(称为辐角)，$\theta$的取值范围是$[0,2\pi)$
\begin{tikzpicture} [global scale=0.6, x=2cm, y=2cm] \draw[->] (0,0) node[left] {$O$} -- (2,0) node[right] {$x$}; \draw[->] (0,0) -- (30:2) node[right] {$P(r,\theta)$} node[pos=0.5, above] {$r$}; \draw[-latex] (0:0.5) to[in=-60,out=90] (30:0.5) node[below right, blue] {$\theta$}; \end{tikzpicture}

则数组$(r, \theta)$可以确定点$P$在空间的位置，并称为点$P$的极坐标。

在直角坐标$[O;\vec i, \vec j ]$中，取$O$为极点，$x$轴为极轴。 则平面上任意一点$P$的直角坐标$(x,y)$和极坐标$(r,\theta)$的变换关系为

\[\begin{cases} x=r\cos\theta \\ y=r\sin\theta \end{cases}, \quad \begin{cases} r=\sqrt{x^2+y^2} \\ \theta=\arctan\frac{y}x \end{cases} \]

$P$的位置向量可以表示为

\[\vec r=x\vec i+y\vec j=r\cos\theta\vec i+r\sin\theta\vec j \]
\begin{tikzpicture} [global scale=0.6, x=2cm, y=2cm] \draw[->] (0,0) node[left] {$O$} -- (2,0) node[right] {$x$}; \draw[->] (0,0) -- (30:2) node[right] {$P(r,\theta)$} node[pos=0.5, above] {$r$}; \draw[-latex] (0:0.5) to[in=-60,out=90] (30:0.5) node[below right, blue] {$\theta$}; \end{tikzpicture}

极坐标下，平面上的曲线可以表示为 $f(r,\theta)=0$, 或者$ r=r(\theta)$

例 4. 易知，

  • $r=1$是平面上以$O$为圆心，半径为$1$的圆，
  • $\theta=\frac{\pi}6$是从$O$出发，沿$(\cos(\frac{\pi}6),\sin(\frac{\pi}6)$方向的射线。

例 5. 圆$(x-1)^2+y^2=1$的极坐标表示为？

\[r=2\cos(\theta), \theta\in[-\frac{\pi}2,\frac{\pi}2] \]
\begin{tikzpicture} [global scale=0.6, x=2cm, y=2cm] \draw[->] (0,0) node[left]{$O$}--(2.5,0) node[right]{$x$}; \draw (1,0) node[below]{$1$} circle(1); \node at (0,0)[fill,circle,inner sep=1.5pt] {}; \node at (1,0)[fill,circle,inner sep=1.5pt] {}; \draw (0:0.5) to[in=-60, out=90] node[right, blue] {$\theta$} (30:0.5); \draw (0,0) --node[above]{$r$} (30:{2*cos(30)}) node[right] {$P(x,y)$}; \draw[dashed] (2,0) -- (30:{2*cos(30)}); \end{tikzpicture}

柱坐标系

在空间坐标系$[O;\vec i, \vec j, \vec k]$中，将$Oxy$平面坐标换成极坐标。

定义 2.
即空间中点$P(x,y,z)$用坐标$P(r, \theta, z)$来表示，其中

\[x=r\cos\theta, \quad y=r\sin\theta, \quad z=z \]

其中$r\geq 0$, $\theta\in[0,2\pi)$, $z\in\mathbb{R}$。

这样给出了空间的柱坐标系。 $(r, \theta, z)$称为点$P$的柱坐标。

例 6. 在柱坐标中，

  • $r=c$表示一个圆柱面，
  • $\theta=\theta_0$表示以$z$轴为边的半平面。
\begin{tikzpicture} [global scale=0.6, y={(1.5*0.907cm,-1.5*0.174cm)},x={(-1.5*0.806cm,-1.5*0.423cm)},z={(0cm,2cm)}] \draw[->] (0,0,0) node[left] {$O$} -- (2,0,0) node[left] {$x$}; \draw[->] (0,0,0) -- (0,2,0) node[right] {$y$}; \draw[->] (0,0,0) -- (0,0,2) node[right] {$z$}; \draw[-latex] (0,0,0) -- (1,2,2); \draw[dashed] (1,2,0) -- (1,2,2) node[right] {$P(r,\theta,z)$} node[pos=0.5, right, red]{$z$}; \node at (1,2,2) [circle,fill,inner sep=1.5pt] {}; \draw[dashed] (0,0,0) -- (1,2,0) node[right] {$P_1$} node[pos=0.5, below, red] {$r$}; \draw[->] (0.5,0,0) to[in=210,out=-30] (0.2,0.4,0) node[below left, red] {$\theta$}; \end{tikzpicture}

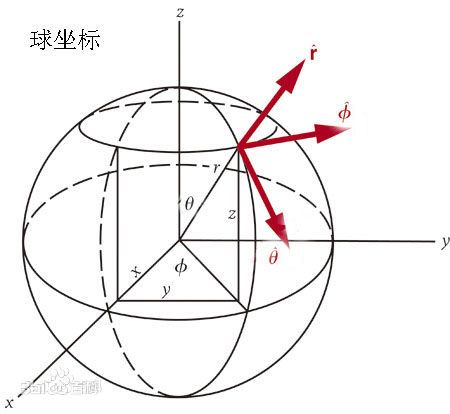
球坐标系

设位置向量$\overrightarrow{OP}$与$z$轴的夹角为$\theta$， $\overrightarrow{OP}$在$Oxy$平面上的投影向量是$\overrightarrow{OP_1}$， 则有

\[\begin{aligned} z=&|OP|\cos\theta, \\ \vec r=&\overrightarrow{OP} \\ =&\overrightarrow{OP_1}+\vec k|OP|\cos\theta \end{aligned} \]
\begin{tikzpicture} [global scale=0.8] \begin{axis} [ view={110}{20}, axis lines=middle, width=7cm, ztick=\empty,ytick=\empty,xtick=\empty, %xlabel=$x$, %zlabel={$z$} ] \addplot3[ domain=0:90, samples = 60, samples y=0, %thick, ] ({cos(x)}, {sin(x)}, 0); \addplot3[ domain=0:90, samples = 60, samples y=0, %thick, ] (0, {cos(x)}, {sin(x)}); \addplot3[ domain=0:90, samples = 60, samples y=0, %thick, ] ({cos(x)}, 0, {sin(x)}); \addplot3[line legend] coordinates { (-0.1,0,0) (1.3,0,0) } node[left] {$x$}; \addplot3[->] coordinates { (0,-0.1,0) (0,1.3,0) } node[right] {$y$}; \addplot3[->] coordinates { (0,0,-0.1) (0,0,1.3) } node[above] {$z$}; % \addplot3[dashed, blue] coordinates { (0,0,0) ({sin(45)},{cos(45)},0) }; \addplot3[ domain=0:90, samples = 60, samples y=0, dashed, blue, ] ({sin(x)*cos(45)}, {sin(x)*sin(45)}, {cos(x)}); \addplot3[ domain=0:90, samples = 60, samples y=0, blue, ] ({sin(30)*cos(x)}, {sin(30)*sin(x)}, {cos(30)}); \addplot3[-latex] coordinates { (0,0,0) ({sin(30)*cos(45)}, {sin(30)*sin(45)}, {cos(30)}) } node[above] {$P$} node[pos=0.5, below] {$\rho$}; \addplot3[-latex] coordinates { ({sin(30)*cos(45)}, {sin(30)*sin(45)+0.1}, {cos(30)}) ({sin(30)*cos(45)}, {sin(30)*sin(45)}, {cos(30)}) } node[pos=0, right] {$(\rho,\theta,\phi)$}; \addplot3[ domain=0:30, samples = 5, samples y=0, blue, -latex, ] ({0.2*sin(x)*cos(45)}, {0.2*sin(x)*sin(45)}, {0.2*cos(x)}) node[pos=0.5, above] {$\theta$}; \addplot3[ domain=0:45, samples = 5, samples y=0, blue, -latex, ] ({0.2*sin(90)*cos(x)}, {0.2*sin(90)*sin(x)}, {0.2*cos(90)}) node[pos=0.5, below] {$\phi$}; \addplot3[red] coordinates { ({sin(30)*cos(45)}, {sin(30)*sin(45)}, {cos(30)}) ({sin(30)*cos(45)}, {sin(30)*sin(45)}, 0) } node[pos=1, below] {$P_1$} node[pos=0.5, right] {$z$}; \addplot3[red] coordinates { ({sin(30)*cos(45)}, {sin(30)*sin(45)}, 0) (0, {sin(30)*sin(45)}, 0) } %({sin(30)*cos(45)}, 0, 0) } node[pos=1, above] {$P_2$} node[pos=0.5, below] {$x$}; \addplot3[red] coordinates { (0, {sin(30)*sin(45)}, 0) (0, 0, 0) } node[pos=1, above left, black] {$O$} node[pos=0.5, above] {$y$}; \end{axis} \end{tikzpicture}

将$P_1$用$xy$平面的极坐标来表示，设辐角是$\phi$，则有

\[\overrightarrow{OP_1}=\vec i|OP_1|\cos\phi+\vec j|OP_1|\sin\phi \]

记$r=|OP|=|\vec r|$，则$|OP_1|=r\sin\theta$，从而有

\[\vec r=r\sin\theta\cos\phi\vec i+r\sin\theta\sin\phi\vec j+r\cos\theta\vec k \]

即有

\[\begin{cases} x=r\sin\theta\cos\phi \\ y=r\sin\theta\sin\phi \\ z=r\cos\theta \end{cases} \]

其中$r\geq 0$, $\theta\in[0,\pi]$, $\phi\in[0,2\pi)$。

\begin{tikzpicture} [global scale=0.8] \begin{axis} [ view={110}{20}, axis lines=middle, width=7cm, ztick=\empty,ytick=\empty,xtick=\empty, %xlabel=$x$, %zlabel={$z$} ] \addplot3[ domain=0:90, samples = 60, samples y=0, %thick, ] ({cos(x)}, {sin(x)}, 0); \addplot3[ domain=0:90, samples = 60, samples y=0, %thick, ] (0, {cos(x)}, {sin(x)}); \addplot3[ domain=0:90, samples = 60, samples y=0, %thick, ] ({cos(x)}, 0, {sin(x)}); \addplot3[line legend] coordinates { (-0.1,0,0) (1.3,0,0) } node[left] {$x$}; \addplot3[->] coordinates { (0,-0.1,0) (0,1.3,0) } node[right] {$y$}; \addplot3[->] coordinates { (0,0,-0.1) (0,0,1.3) } node[above] {$z$}; % \addplot3[dashed, blue] coordinates { (0,0,0) ({sin(45)},{cos(45)},0) }; \addplot3[ domain=0:90, samples = 60, samples y=0, dashed, blue, ] ({sin(x)*cos(45)}, {sin(x)*sin(45)}, {cos(x)}); \addplot3[ domain=0:90, samples = 60, samples y=0, blue, ] ({sin(30)*cos(x)}, {sin(30)*sin(x)}, {cos(30)}); \addplot3[-latex] coordinates { (0,0,0) ({sin(30)*cos(45)}, {sin(30)*sin(45)}, {cos(30)}) } node[above] {$P$} node[pos=0.5, below] {$\rho$}; \addplot3[-latex] coordinates { ({sin(30)*cos(45)}, {sin(30)*sin(45)+0.1}, {cos(30)}) ({sin(30)*cos(45)}, {sin(30)*sin(45)}, {cos(30)}) } node[pos=0, right] {$(\rho,\theta,\phi)$}; \addplot3[ domain=0:30, samples = 5, samples y=0, blue, -latex, ] ({0.2*sin(x)*cos(45)}, {0.2*sin(x)*sin(45)}, {0.2*cos(x)}) node[pos=0.5, above] {$\theta$}; \addplot3[ domain=0:45, samples = 5, samples y=0, blue, -latex, ] ({0.2*sin(90)*cos(x)}, {0.2*sin(90)*sin(x)}, {0.2*cos(90)}) node[pos=0.5, below] {$\phi$}; \addplot3[red] coordinates { ({sin(30)*cos(45)}, {sin(30)*sin(45)}, {cos(30)}) ({sin(30)*cos(45)}, {sin(30)*sin(45)}, 0) } node[pos=1, below] {$P_1$} node[pos=0.5, right] {$z$}; \addplot3[red] coordinates { ({sin(30)*cos(45)}, {sin(30)*sin(45)}, 0) (0, {sin(30)*sin(45)}, 0) } %({sin(30)*cos(45)}, 0, 0) } node[pos=1, above] {$P_2$} node[pos=0.5, below] {$x$}; \addplot3[red] coordinates { (0, {sin(30)*sin(45)}, 0) (0, 0, 0) } node[pos=1, above left, black] {$O$} node[pos=0.5, above] {$y$}; \end{axis} \end{tikzpicture}

称$(r,\theta,\phi)$为$P$的球坐标，形成的坐标系是球坐标系。

例 7. 球$x^2+y^2+(z-1)^2=1$的一些其它表示方式

  1. 球坐标表示
    \[\rho = 2\cos(\theta), \theta\in[-\frac{\pi}2, \frac{\pi}2] \]
  2. 参数表示
    \[\begin{cases} x = 1 \sin\theta\cos\alpha \\ y = 1 \sin\theta\sin\alpha \\ z = 1 + 1\cos\theta \end{cases} \]
    \[\theta\in[0,\pi], \alpha\in[0,2\pi] \]
\begin{tikzpicture} [global scale=0.8] \begin{axis} [ view={110}{20}, axis lines=middle, width=7cm, ztick=\empty,ytick=\empty,xtick=\empty, %xlabel=$x$, %zlabel={$z$} ] \addplot3[ domain=0:360, samples = 100, samples y=0, %thick, ] (0, {0.5*cos(x)}, {0.5+0.5*sin(x)}); \addplot3[->] coordinates { (0,0,0) (1.3,0,0) } node[left] {$x$}; \addplot3[->] coordinates { (0,-0.1,0) (0,0.8,0) } node[right] {$y$}; \addplot3[->] coordinates { (0,0,-0.1) (0,0,1.3) } node[above] {$z$}; \addplot3 coordinates { (0,0,0) (0,0,0.5) } node[left] {$1$}; % \addplot3[ domain=-90:90, samples = 60, samples y=0, blue, ] ({0.5*cos(x)}, {0.5*sin(x)}, 0.5); \addplot3[ domain=90:270, samples = 60, samples y=0, dashed, blue, ] ({0.5*cos(x)}, {0.5*sin(x)}, 0.5); \addplot3[-latex] coordinates { (0,0,0) (0, {0.5*cos(45)}, {0.5+0.5*sin(45)}) } node[above] {$P$} node[pos=0.5, above] {$\rho$}; \addplot3[-latex] coordinates { (0, {0.5*cos(45)+0.1}, {0.5+0.5*sin(45)}) (0, {0.5*cos(45)}, {0.5+0.5*sin(45)}) } node[pos=0, right] {$(\rho,\theta,\phi)$}; \addplot3[ domain=0:30, samples = 5, samples y=0, blue, -latex, ] (0, {0.2*sin(x)*sin(45)}, {0.2*cos(x)}) node[pos=0.5, above] {$\theta$}; \end{axis} \end{tikzpicture}

参数方程

平面上圆$x^2+y^2=4$的参数表示

\[\begin{cases} x=2\cos\theta \\ y=2\sin\theta \end{cases}, \theta\in[0,2\pi) \]

平面上椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的参数表示

\[\begin{cases} x=a\cos\theta \\ y=b\sin\theta \end{cases}, \theta\in[0,2\pi) \]

类似可以得到空间球面及椭球面的参数表示

空间中，球面$(x-a)^2+(y-b)^2+c^2=4$的参数表示

\[\begin{cases} x=a+2\sin\theta\cos\phi \\ y=b+2\sin\theta\sin\phi \\ z=2\cos\theta \end{cases}, \theta\in[0,\pi], \phi\in[0,2\pi) \]

空间中椭球面$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$的参数表示

\[\begin{cases} x=a\sin\theta\cos\phi \\ y=b\sin\theta\sin\phi \\ z=c\cos\theta \end{cases}, \theta\in[0,\pi], \phi\in[0,2\pi) \]

例 8. 通过两曲面$x^2+y^2+4z^2=1$和$x^2=y^2+z^2$的交线，而母线平行于$z$轴的柱面方程。 GeogeBra

解. 母线平行于$z$轴，则所求柱面与$Oxy$平面的交线$F(x,y)=0$就是所求的柱面方程。

而$F(x,y)=0$是曲线在$Oxy$平面的投影。将曲线方程

\[\begin{cases} x^2+y^2+4z^2=1 \\ x^2=y^2+z^2 \\ \end{cases} \]

消去变量$z$即为曲线在$Oxy$平面上的投影

得到

\[x^2+y^2+4(x^2-y^2)=1 \]

为双曲线$5x^2-3y^2=1$，也是所求的柱面方程。

例 9. 已知球面过点$(0,-3,1)$且与$Oxy$平面的交为圆$\begin{cases} x^2+y^2=16 \\ z=0 \end{cases}$。求球面的方程

解. 球与平面的相交为圆，且球心在平面的过圆心的法线上。

由题意，球心的坐标为$(0,0,z_0)$。

同时，球心与点$(0,-3,1)$及圆周上的任意一点（如$(0,4,0)$）的距离相等，

\[\begin{aligned} (0-0)^2+(-3-0)^2+(1-z_0)^2 \\ =(0-0)^2+(4-0)^2+(0-z_0)^2 \end{aligned} \]

得到

\[10-2z_0=16, \quad \Rightarrow z_0=-3 \]

球心为$(0,0,-3)$，半径为$\sqrt{3^2+4^2}=5$

例 10. 求直线$l$在平面$\pi$上的投影直线$l_0$的方程， 并求$l_0$绕$y$轴旋转一周所成的曲面的方程。

\[l: \frac{x-1}1=y=\frac{z-1}{-1}, \quad \pi: x-y+2z-1=0 \]
\begin{tikzpicture}[global scale=0.6] \coordinate[label=below:$P_1$] (p1) at (15:3.5); \coordinate (p0) at ($ (p1)+(90:1) $); \coordinate[label=above:$\vec n$] (n) at ($ (p1)+(90:1.5) $); \coordinate[label=below:$P_0$] (p) at ($ (p1)-(10:2) $); \coordinate (A) at (0,0); \coordinate (B) at ($ (A)+(0:4) $); \coordinate (C) at ($ (B)+(45:2) $); \coordinate (D) at ($ (C)-(0:4) $); \draw (A)--(B)-- node[above left, near end]{$\pi$} (C) -- (D)--cycle; \draw[->, blue] (p1) -- (n); \draw[red] (p)--($ (p)!1.2!(p1) $) node[right] {$l_0$}; \draw (p) -- ($ (p)!1.5!(p0) $) node[right] {$l$}; %\draw[thick, -latex] (p1) -- (p0); %\draw[thick, -latex] (p) -- (p0); \end{tikzpicture}

如图，设$l_0$的方向向量为$\vec v_0$，$l$的方向向量为$\vec v$，$\pi$的法向量为$\vec n$。则

  • $\vec v_0\perp \vec n$
  • $\vec v_0$, $\vec n$, $\vec v$共面，即可以设
    \[\vec v_0 = \vec v + \lambda \vec n \]

则$\lambda$满足

\[\vec v\cdot\vec n +\lambda \vec n\cdot\vec n=0 \]

由题设

\[\vec v = (1,1,-1), \quad \vec n = (1, -1, 2) \]

得到$-2+\lambda 6 =0$，即有

\[\vec v_0=(1,1,-1)+\frac13(1,-1,2) =(\frac43, \frac23, -\frac13) \]

可以取方向$\vec v_0=(4,2,-1)$

另外，$l_0$过直线$l$与平面$\pi$的交战$P_0(x_0,y_0,z_0)$，则有

\[\begin{aligned} x_0-1=y_0=\frac{z_0-1}{-1}, \quad x_0-y_0+2z_0-1=0 \end{aligned} \]

得到$P_0=(2,1,0)$

得到投影直线$l_0$，过点$P_0(2,1,0)$，方向$\vec v_0=(4,2,-1)$，它的方程为

\[\frac{x-2}{4}=\frac{y-1}{2}=\frac{z-0}{-1} \]

下面，求$l_0$绕$y$轴旋转得到的曲面的方程。

设$P(x,y,z)$在曲面上，它是由直线$l_0$上的点$Q(x_0,y_0,z_0)$旋转得到。

  • 取转轴($y$轴)上的任意一点$O$，如$O=(0,0,0)$
  • 有$|OP| = |OQ|$
  • $\overrightarrow{OP}$与转轴($y$轴)垂直

可以得到

\[\begin{aligned} x^2+y^2+z^2=x_0^2+y_0^2+z_0^2, \quad (*) \\ (x-x_0, y-y_0, z-z_0)\cdot(0,1,0)=0, \Rightarrow y=y_0 \end{aligned} \]

由$Q(x_0,y_0,z_0)$在$l_0$上，

\[\frac{x_0-2}{4}=\frac{y_0-1}{2}=\frac{z_0-0}{-1} \]

将$y=y_0$代入上式，有

\[x_0=2+2(y-1), z_0=-\frac{y-1}2 \]

代入(*)式，可以得到旋转面方程为

\[x^2+y^2+z^2=(2y)^2+y^2+\left(\frac{y-1}2\right)^2 \]

整理后，得到

\[4x^2+4y^2-17\left(y-\frac1{17}\right)^2=\frac{16}{17} \]

为单叶双曲面。

谢谢

ball-coordinate-ustc

沪科版

在曲线上取两点$M$和$M'$，其横坐标分别为$x$与$x+dx$， 则两点的距离为

目录

本节读完

例 11. 谢

11.

求过点(0,-3,1)且与Oxy平面的交为圆的球面的方程

https://mooc1-api.chaoxing.com/ananas/latex/render?callback=jQuery1720304907071950090371646293920428&formula=x%5E2%2By%5E2%2B4z%5E2%3D1&=1646293944636