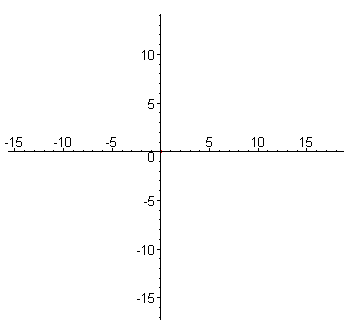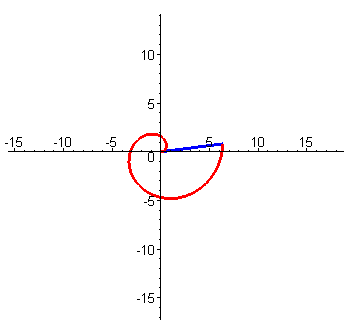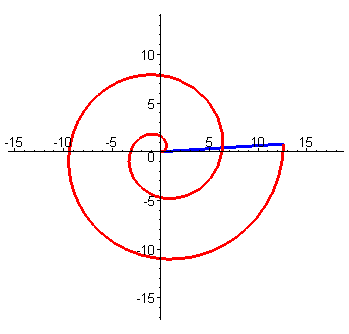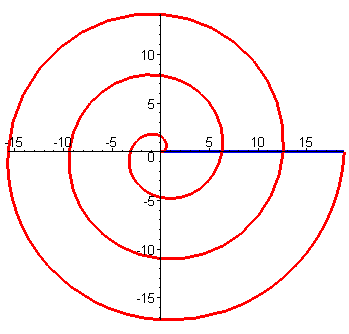3. 函数极限

极限

张瑞
中国科学技术大学数学科学学院

函数极限

函数

函数，就是量与量之间的关系

定义 1.
设$D\subset\mathbb{R}$为非空数集，若有某种确定的对应关系$f$，对于每个$x\in D$，都有唯一的一个实数$y$与其对应，则称这个对应关系$f$是$D$上的一个实值函数，记为$y=f(x)$，或$f:D\to\mathbb{R}$。$D$称为$f$的定义域。$x$称为自变量，$y$称为因变量，$f(x)$称为函数在$x$处的值。$f$的所有的值的集合叫做$f$的值域，通常记为$f(D)$，即 $f(D)=\{y|y=f(x), x\in D\}$。

  1. 函数有三个基本要素：定义域、值域、单值的对应关系。
  2. 函数$y=f(x)$可以在二维的坐标平面上用图像表示出来
  1. 若函数的值域$f(D)$是一个有界集合，即存在$M>0$，满足$|f(x)|\leq M$, $\forall x\in D$。则称函数$f$为$D$上的有界函数，或者$f$在$D$上有界。
  2. 若$\forall x_1<x_2\in D$，有$f(x_1)\leq f(x_2)$，则称函数为单调增函数。
  3. 若$\forall x_1<x_2\in D$，有$f(x_1)\geq f(x_2)$，则称函数为单调减函数。
  4. 若$\forall y\in f(D)$，都有唯一确定的$x\in D$使得$f(x)=y$。则称$f$是一一映射。此时，可以很自然的导出$f(D)$到$D$的映射，这个映射称为$f(x)$的反函数或逆映射，记为$f^{-1}$，或$x=f^{-1}(y)$。

不同的函数在它们的公共有定义的区域内可以进行四则运算：

  • $(f\pm g)(x)=f(x)\pm g(x)$
  • $(f\cdot g)(x)=f(x)g(x)$
  • $\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}$, 当$g(x)\neq 0$

定义 2.
函数$y=f(u)$，$u\in B$。函数$u=g(x)$，$x\in A$。若函数$g(x)$的值域$g(A)$包含在$B$内，即$g(A)\subset B$，则

\[(f\circ g)(x)=f(g(x)) , x\in A \]

定义了一个新函数$f\circ g$，称为$f$与$g$的复合函数，它的定义域是$A$，通常记为$y=f(g(x))$，$u$为中间变量。

  1. 注意$f\circ g$与$g\circ f$通常不同。
  2. 复合运算满足结合律：$(f\circ g)\circ h=f\circ(g\circ h)$

常数函数，幂函数，指数函数，对数函数，三角函数与反三角函数，称为基本初等函数。由基本初等函数经过有限次四则运算和复合运算得出的函数称为初等函数。

多项式函数： $f(x)=a_0+a_1x+\cdots+a_nx^n$

有理函数： $\frac{f(x)}{g(x)}$，其中$f(x)$和$g(x)$均为多项式

幂函数： $f(x)=x^a$，$a$为任意的实数

双曲函数：

\[\sinh(x)=\frac{e^{x}-e^{-x}}2, \cosh(x)=\frac{e^{x}+e^{-x}}2 \]
\[\tanh(x)=\frac{e^{x}-e^{-x}}{e^x+e^{-x}}, \coth(x)=\frac{e^{x}+e^{-x}}{e^x-e^{-x}}, \]

例 1. 双曲函数的特性：

\[\sinh(-x)=-\sinh(x), \cosh(-x)=\cosh(x) \]
\[\sinh(x\pm y)=\sinh(x)\cosh(y)\pm\cosh(x)\sinh(y) \]
\[\cosh(x\pm y)=\cosh(x)\cosh(y)\pm\sinh(x)\sinh(y) \]
\[\cosh^2x-\sinh^2x=1 \]
\[\sinh(2x)=2\sinh(x)\cosh(x), \cosh(2x)=\cosh^2x+\sinh^2x \]

例 2. 双曲正弦函数的反函数为

\[y=\sinh^{-1}x=\ln(x+\sqrt{1+x^2}) \]

函数的表示方法

  • 显式， $y=f(x)$
  • 隐式， $f(x,y)=0$
  • 参数式，$\left\{\begin{aligned} x=\phi(t) \\y=\psi(t) \end{aligned}\right. $
  • 极坐标

常见函数

  • 常值函数： $f(x)\equiv c$
  • 取整函数： $f(x)=[x]$
  • Dirichlet函数:
    \[f(x)=D(x)=\left\{\begin{aligned} 1 &, x\in Q \\ 0 &, x\notin Q \end{aligned}\right. \]
  • Riemann函数:
    \[f(x)=R(x)=\left\{\begin{aligned} \dfrac{1}{p} &, x=\dfrac{q}{p} \in Q \\ 0 &, x \notin Q \end{aligned}\right. \]

阿基米德螺线(Archimedean spiral)

  • $r=a\theta, \theta\in\mathbb{R}$

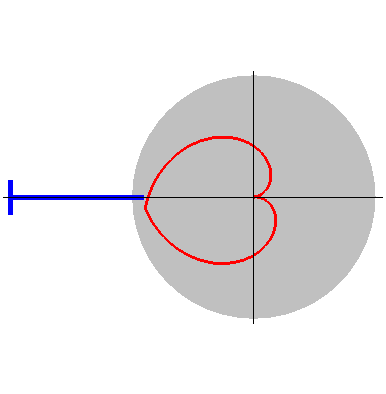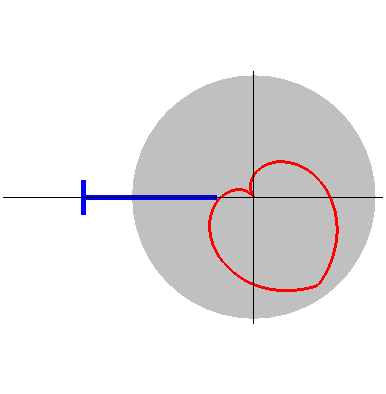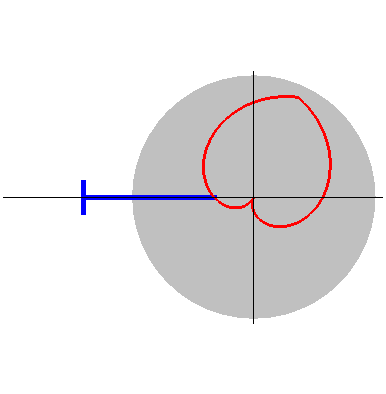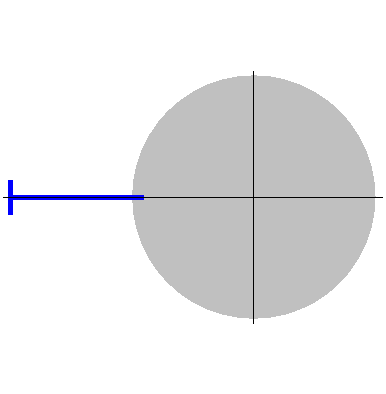
    chap1-spiral-1 chap1-spiral-2

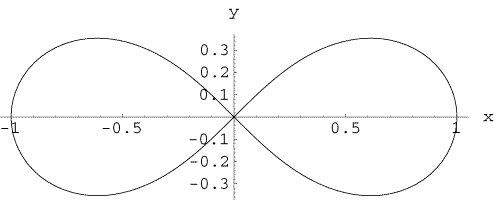
伯努利双纽线 (Lemniscate of Bernoulli)

  • $(x^2+y^2)^2=2a^2(x^2-y^2)$
  • $r^2=2a^2\cos(2\theta)$
  • $x=\dfrac{a\sqrt{2}\cos(t)}{\sin^2(t)+1}, y=\dfrac{a\sqrt 2\cos(t)\sin(t)}{\sin^2(t)+1}$

    chap1-lemniscate

摆线 (cycloid)

  • $x=a(\theta-\sin\theta), y=a(1-\cos \theta)$

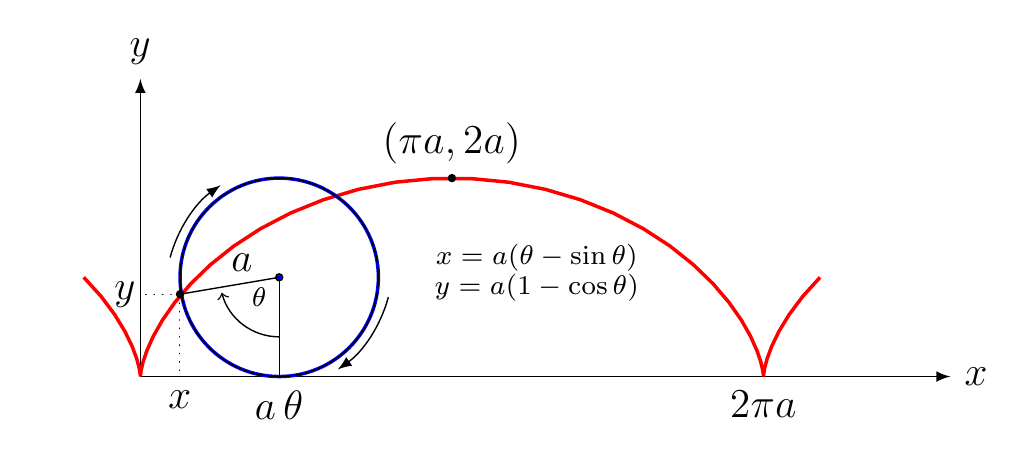
    chap1-cycloid

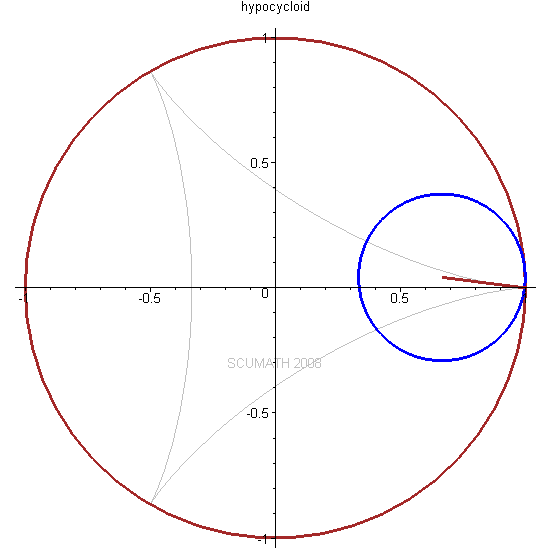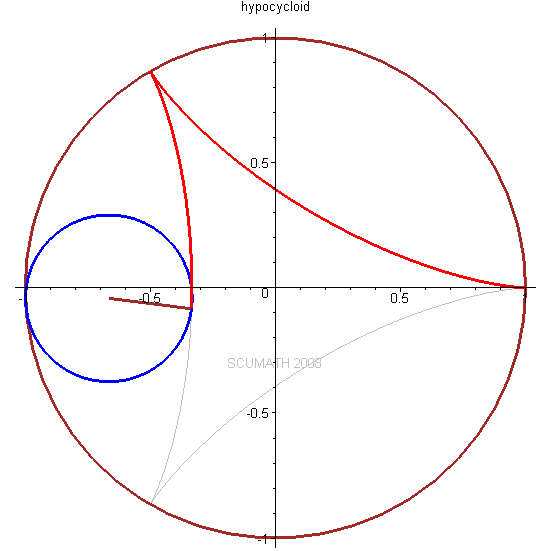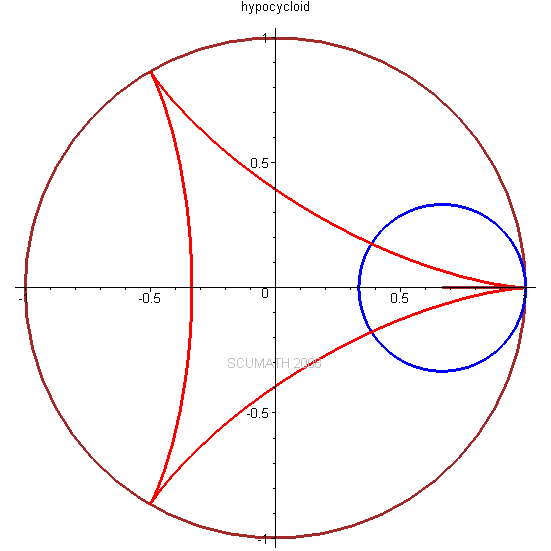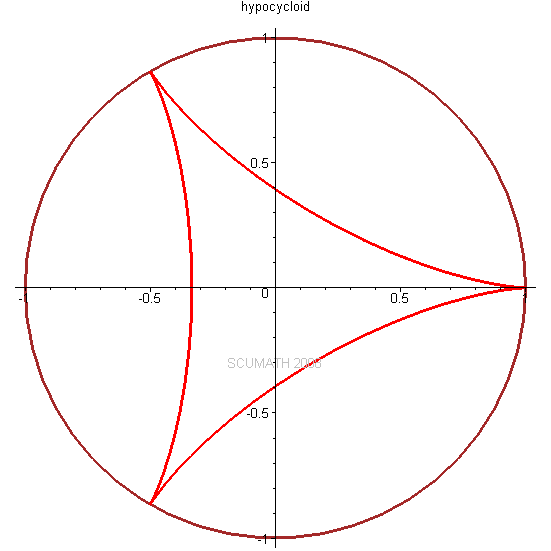
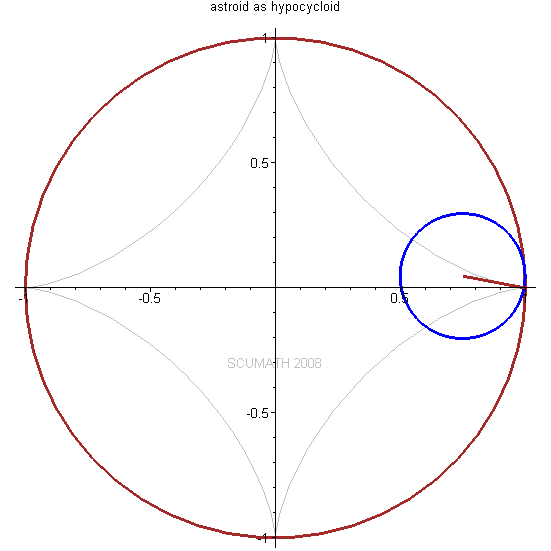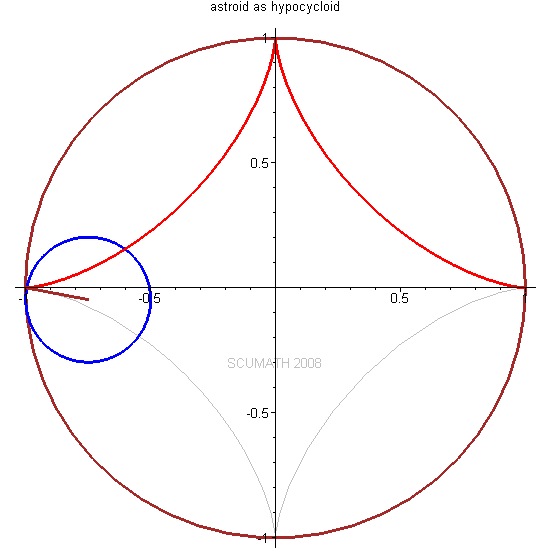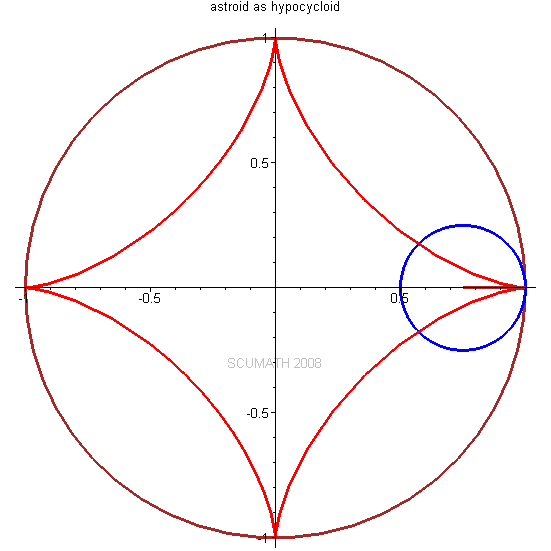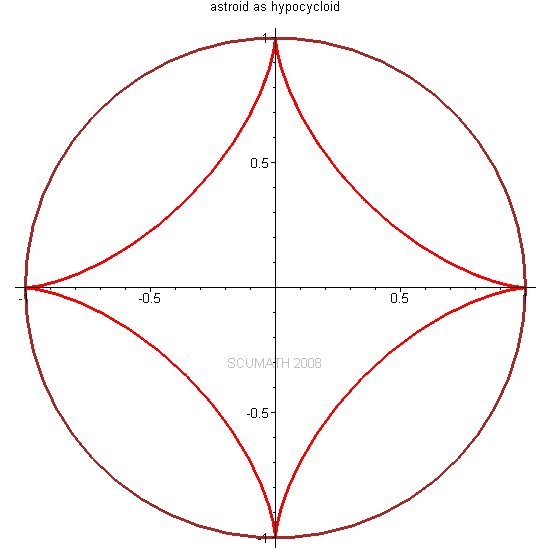
圆内摆线 (Hypocycloid)

  • $\begin{cases}x=(R-r)\cos\theta+r\cos(\dfrac{R-r}r\theta),\\ y=(R-r)\sin\theta-r\sin(\dfrac{R-r}r\theta)\end{cases}$

    chap1-hypocycloid-1 chap1-hypocycloid-2

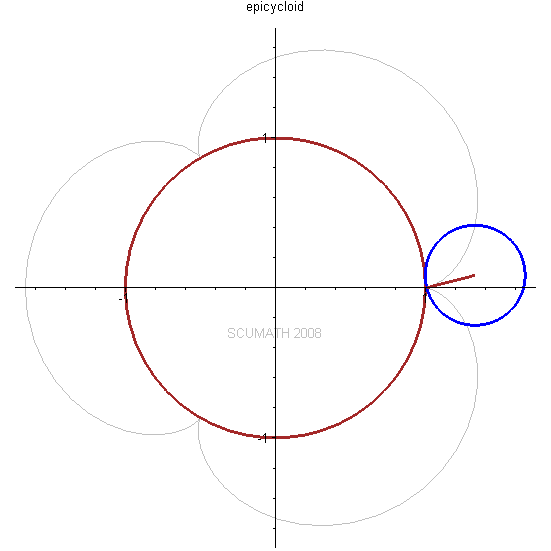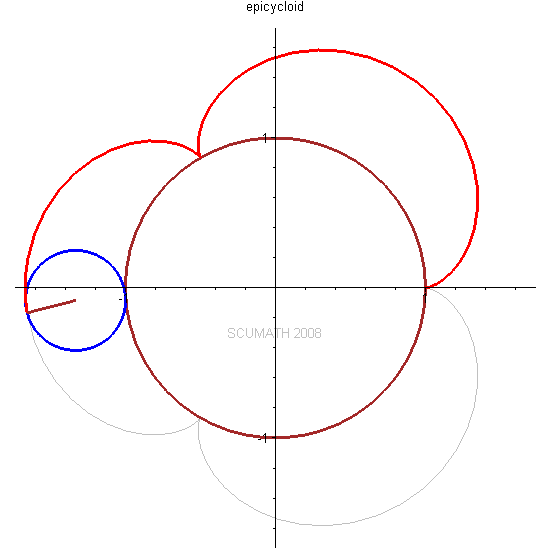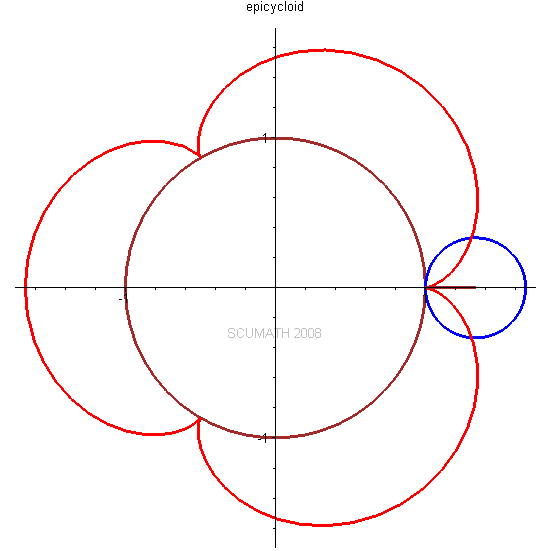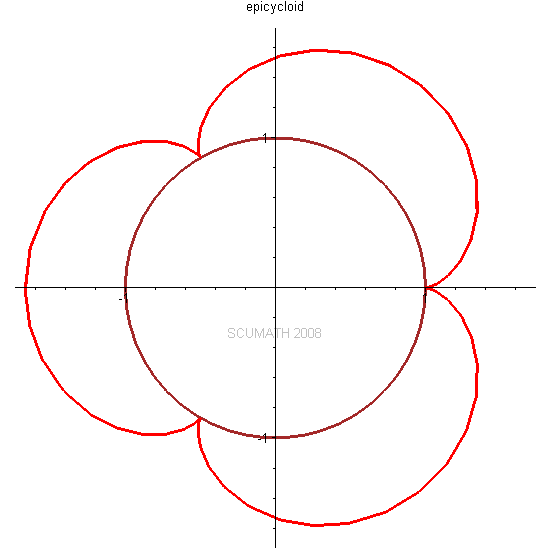
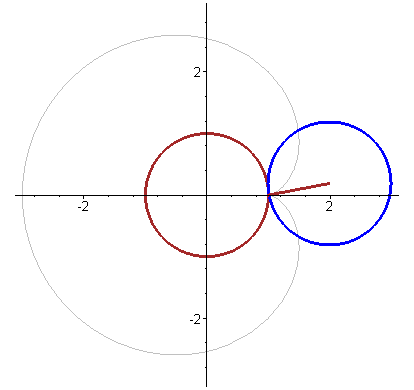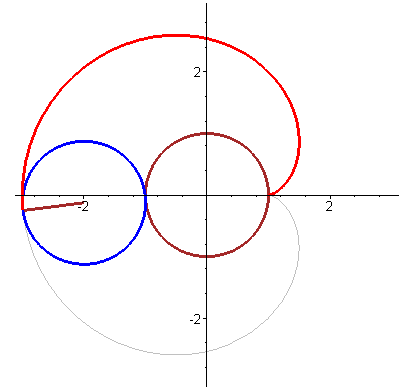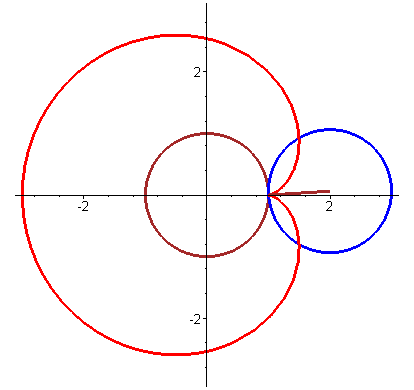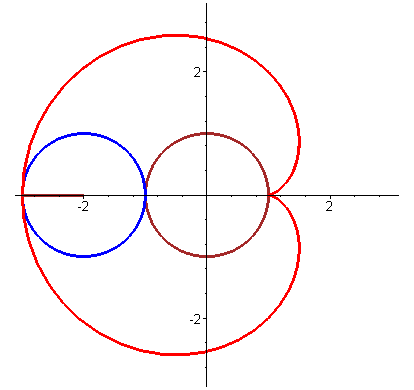
圆外摆线 (epicycloid)

  • $\begin{cases}x=(R+r)\cos\theta+r\cos(\dfrac{R+r}r\theta),\\ y=(R+r)\sin\theta-r\sin(\dfrac{R+r}r\theta)\end{cases}$

    chap1-epicycloid-1 chap1-epicycloid-2

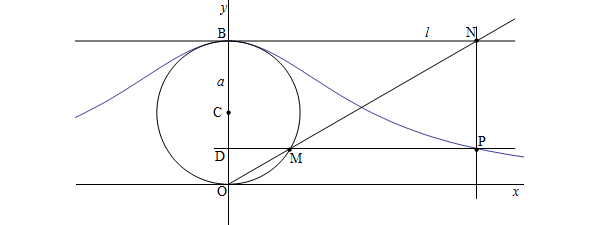
箕舌线 (The Witch of Agnesi)

  • $y=\dfrac{8a^3}{x^2+4a^2}$
  • $x=2a\tan\theta, y=2a\cos^2\theta$

    chap1-witch-agnesi

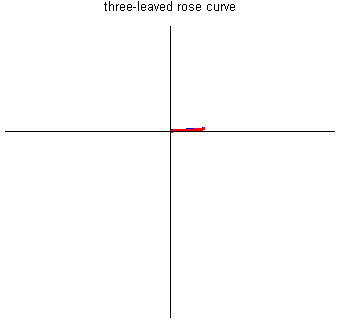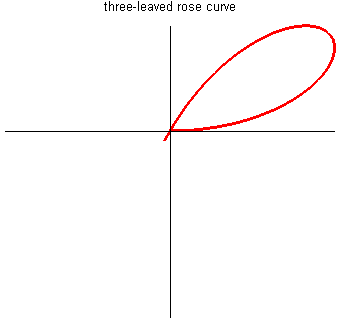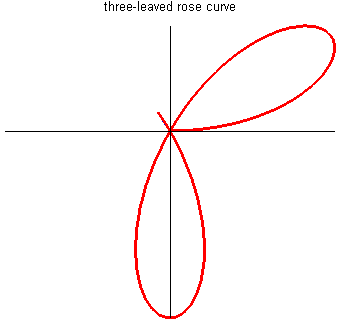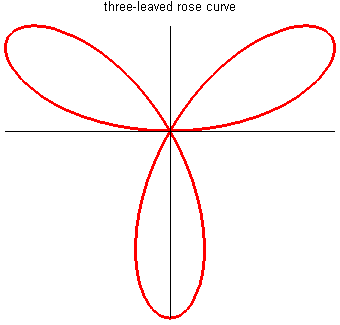
玫瑰线 (Rose Curve)

  • $r=\cos(k\theta)$
  • $x=\cos(k\theta)\cos(\theta) , y=\cos(k\theta)\sin(\theta)$

    chap1-rose-1 chap1-rose-2

函数在无穷大处的极限

定义 3. (函数在$\infty$处的极限)
$f(x)$在$|x|>a>0$上定义，$l$为给定的数。若$\forall \epsilon>0$, $\exists M=M(\epsilon)>a$，满足

\[|f(x)-l|<\epsilon, \forall |x|>M \]

则称$x$趋于$\infty$时，$f(x)$的极限为$l$，记为

\[\lim_{x\to\infty}f(x)=l \]

或

\[f(x)\to l , (x\to\infty) \]

定义 4. (函数在$+\infty$处的极限)
$f(x)$在$[a,+\infty)$上定义，$l$为给定的数。若$\forall \epsilon>0$, $\exists M=M(\epsilon)>|a|$，满足

\[|f(x)-l|<\epsilon, \forall x>M \]

则称$x\to+\infty$时，$f(x)$的极限为$l$，记为

\[\lim_{x\to+\infty}f(x)=l \]

或

\[f(x)\to l , x\to+\infty \]

定义 5. (函数在$-\infty$处的极限)
$f(x)$在$(-\infty,a]$上定义，$l$为给定的数。若$\forall \epsilon>0$, $\exists M=M(\epsilon)>|a|$，满足

\[|f(x)-l|<\epsilon, \forall x<-M \]

则称$x\to-\infty$时，$f(x)$的极限为$l$，记为

\[\lim_{x\to-\infty}f(x)=l \]

或

\[f(x)\to l , x\to-\infty \]
  1. 对$\epsilon$越小的情形越感兴趣，有时可以限制$\epsilon$的一个上界
  2. $M$只要证明存在性，有时候不需具体算出来

例 3. (例1.3.5) 证明 $\displaystyle \lim_{x\to\infty}\frac1{x^k}=0$, 其中$k\in\mathbb{Z}^{+}$

例 4. (例1.3.6) 证明$\displaystyle \lim_{x\to+\infty}a^x=0$, 其中$0<a<1$

例 5. (例1.3.8) 证明

\[\displaystyle \lim_{x\to+\infty}\arctan(x)=\frac{\pi}2 , \displaystyle \lim_{x\to-\infty}\arctan(x)=-\frac{\pi}2 \]

函数在一点处的极限

描述当$x$无限接近$x_0$时，函数$f(x)$无限接近一个数$l$。

定义 6. (函数在一点的极限)
函数$f(x)$在$x_0$的某去心邻域$\{x| 0<|x-x_0|<\eta\}$内定义，对于实数$l$，若$\forall \epsilon>0$， $\exists \delta=\delta(x_0,\epsilon)>0$，满足

\[|f(x)-l|<\epsilon, \forall x\in\{0<|x-x_0|<\delta\} \]

则称$x\to x_0$时，$f(x)$的极限为$l$，记为

\[\lim_{x\to x_0}f(x)=l \]

或

\[f(x)\to l , x\to x_0 \]

称为$\epsilon$-$\delta$语言。

  1. 对$\epsilon$越小的情形越感兴趣，有时可以限制$\epsilon$的一个上界
  2. $\delta$也是越小越好，因此可以限制$\delta$的一个上界
  3. 函数$f(x)$可以在$x_0$处没有定义，仍然可以有极限

例 6. (例1.3.10) 求$\displaystyle \lim_{x\to0}x\sin\frac1x$

例 7. (例1.3.11) 证明$\displaystyle \lim_{x\to1}\frac{x^2-1}{x^2-x}=2$

例 8. 证明$\displaystyle \lim_{x\to1}\ln x=0$

例 9. 已知$a>1$时，$\displaystyle\lim_{n\to\infty}a^{\frac1n}=1$，求$\displaystyle\lim_{x\to0}a^x$

只需要说明$\delta$的存在

例 10. 证明$\displaystyle\lim_{x\to 0}R(x)=0$，其中$R(x)$为Riemann函数

\[R(x)=\left\{\begin{aligned} \dfrac{1}{p} &, x=\dfrac{q}{p} \in Q, p, q \mbox{ are coprime numbers} \\ 0 &, x \notin Q \end{aligned}\right. \]

定义 7. (函数的左、右极限)
函数$f(x)$在$x_0$的左邻域$\{x|x_0-\eta<x<x_0\}$内有定义，$l$是给定的数。若对$\forall \epsilon>0$, $\exists\delta=\delta(\epsilon,x_0)\in(0,\eta)$，使得

\[|f(x)-l|<\epsilon, \forall x_0-\delta<x<x_0 \]

则称$f(x)$在$x_0$左极限为$l$，记为

\[\lim_{x\to x_0^-}f(x)=l \]

或者

\[f(x_0^-)=l \]

类似，可以定义函数$f(x)$的右极限，将右极限记为

\[\lim_{x\to x_0^+}f(x)=l , \ \ \ \ f(x_0^+)=l \]

定理 1.
函数$f(x)$在$x_0$的去心邻域有定义，则$\displaystyle\lim_{x\to x_0}f(x)$存在的充要条件是，$f(x)$在$x_0$的单侧极限$\displaystyle\lim_{x\to x_0^-}f(x)$和$\displaystyle\lim_{x\to x_0^+}f(x)$都存在且相等

证明是显然的。

可以依据这个定理来判断函数$f(x)$在$x_0$有没有极限。

例 11. 符号函数

\[\mbox{sgn}(x)=\left\{\begin{aligned} & 1, x>0 \\ & 0, x=0 \\ & -1, x<0 \end{aligned} \right. \]

在$0$处左、右极限

例 12. (例1.3.12) 证明$\displaystyle\lim_{x\to0}a^x=1$，其中$a>1$。

函数极限的性质与四则运算

函数的极限有6种形式，$x\to+\infty$, $x\to-\infty$, $x\to\infty$, $x\to x_0$, $x\to x_0^-$, $x\to x_0^+$，以$x\to x_0$为例来描述。

定理 2. (函数极限的唯一性)
函数极限如果存在，则唯一

定理 3. (局部有界性)
若函数极限$\displaystyle\lim_{x\to x_0}f(x)$存在，则$f(x)$在$x_0$附近有界。即存在$\delta>0$和$M>0$，使得

\[|f(x)|<M, \forall x\in\{x|0<|x-x_0|<\delta\} \]

定理 4. (函数极限的比较定理)
设$\displaystyle\lim_{x\to x_0}f(x)=l_1$, $\displaystyle\lim_{x\to x_0}g(x)=l_2$,

(1) 如果在$x_0$附近有$f(x)\geq g(x)$，则$l_1\geq l_2$

(2) 如果$l_1>l_2$，则在$x_0$附近有$f(x)>g(x)$

定理 5. (函数极限的保号性)
设$\displaystyle\lim_{x\to x_0}f(x)=l$,

(1) 如果在$x_0$附近有$f(x)\geq 0$，则$l\geq 0$

(2) 如果$l>0$，则在$x_0$附近有$f(x)>0$

(3) 如果$a<l<b$，则在$x_0$附近有$a<f(x)<b$

定理 6. (函数极限的四则运算法则)
设$\displaystyle\lim_{x\to x_0}f(x)=l_1$, $\displaystyle\lim_{x\to x_0}g(x)=l_2$,

(1) 函数$f(x)\pm g(x)$的极限也存在，且有

\[\lim_{x\to x_0}(f(x)\pm g(x))=l_1\pm l_2=\lim_{x\to x_0}f(x)\pm\lim_{x\to x_0}g(x) \]

(2) 乘积函数$f(x)g(x)$的极限也存在，且

\[\lim_{x\to x_0}f(x) g(x)=l_1 l_2 \]

特别地，对任意常数$c$，有

\[\lim_{x\to x_0}c f(x)=c l_1 \]

(3) 若$l_2\neq 0$，则函数$\frac{f(x)}{g(x)}$的极限也存在，且

\[\lim_{x\to x_0}\frac{f(x)}{g(x)}=\frac{l_1}{ l_2} \]

例 13. 若$p_n(x)$是次数不高于$n$次的多项式，则对任意数$a$，有$\displaystyle\lim_{x\to a}p_n(x)=p_n(a)$

例 14. (例1.3.16) $\displaystyle\lim_{x\to-1}(\frac{1}{x+1}-\frac{3}{x^3+1})$

例 15. 求$\displaystyle\lim_{x\to 0}\frac{(1+x)^{\frac{n}m}-1}x$

定理 7. (复合函数的极限)
设函数$f(x)$在$x_0$的某个去心邻域内有定义，$\displaystyle\lim_{x\to x_0}f(x)$存在；又设$x=\phi(t)$， $\displaystyle\lim_{t\to t_0}\phi(t)=x_0$，且在$t_0$附近，有

\[\phi(t)\neq x_0, \forall t\neq t_0 \]

则有

\[\lim_{t\to t_0}f(\phi(t))=\lim_{x\to x_0}f(x) \]

由$\displaystyle\lim_{x\to x_0}f(x)$存在，设为$l$。则

${\color{blue}\forall \epsilon>0}$，存在$\eta>0$，满足

\[|f(x)-l|<\epsilon, \forall 0<|x-x_0|<\eta \]

又$\displaystyle\lim_{t\to t_0}\phi(t)=x_0$， 则对$\eta>0$，存在$\delta_1>0$，满足

\[|\phi(t)-x_0|<\eta, \forall 0<|t-t_0|<\delta_1 \]

因为在$t_0$附近$\phi(t)\neq x_0$， 则存在$\delta_2>0$，有

\[|\phi(t)-x_0|>0, \forall 0<|t-t_0|<\delta_2 \]

取${\color{blue}\delta=\min(\delta_1,\delta_2)}$，则

\[{\color{red}0<}|\phi(t)-x_0|<\eta, \forall 0<|t-t_0|<\delta \]

因此，有

\[|f(\phi(t))-l|<\epsilon, \forall 0<|t-t_0|<\delta \]

复合函数求极限的过程，相当于“变量代换”。

  • 若函数$F(x)$可以写成$F(x)=f(\phi(x))$，且有
    \[\lim_{x\to x_0}\phi(x)=t_0, \quad \lim_{t\to t_0}f(t)=l \]
    若$\phi(x)$在$x_0$附近是一个单调函数，则有
    \[\lim_{x\to x_0}f(\phi(x))=\lim_{t\to t_0}f(t)=l \]

例 16. (例1.3.17) 设$a>0$，证明$\displaystyle\lim_{x\to x_0}a^x=a^{x_0}$

例 17. 对任意$a>0$，有$\displaystyle \lim_{x\to a}\ln x=\ln a$

复合函数求导中，注意条件

例 18. 取$f(x)=\begin{cases} 1, x\neq 0\\ 0, x=0\end{cases}$，$R(x)=\begin{cases} \frac1q, x=\frac{p}q \\ 0, x\notin\mathbb{Q} \end{cases}$。 可以得到$\displaystyle\lim_{x\to 0}f(x)=1$， $\displaystyle\lim_{t\to a}R(t)=0$, $a$为任意实数。

求$\displaystyle\lim_{t\to a}f(R(t))$。

解.

\[f(R(t))=\begin{cases} 1, x=\frac{p}{q}\\0, x\notin\mathbb{Q}\end{cases} \]

在任意点的极限都不存在。

例 19. 若$\displaystyle\lim_{x\to x_0}f(x)=a$，则$\displaystyle\lim_{x\to x_0}e^{f(x)}=e^a$

例 20. 若$\displaystyle\lim_{x\to x_0}f(x)=a>0$，则$\displaystyle\lim_{x\to x_0}\ln {f(x)}=\ln a$

命题 1.
已知$\displaystyle\lim_{x\to a}f(x)=A$, $\displaystyle\lim_{x\to a}g(x)=B$。 若$A>0$，则有

\[\lim_{x\to a} f(x)^{g(x)}=A^B \]

定理 8. (函数极限与数列极限的关系)
函数$f(x)$在$x_0$的某个去心邻域内定义，则$\displaystyle\lim_{x\to x_0}f(x)=l$的充要条件是，任意以取值异于$x_0$而以$x_0$为极限的数列$\{x_n\}$，都有$\displaystyle\lim_{n\to\infty}f(x_n)=l$

注. 实际上，若有对任意取值异于$x_0$而收敛到$x_0$的序列$\{x_n\}$，$\displaystyle\lim_{n\to\infty}f(x_n)$都存在，则可以证明这些极限值是同一个。

注. 这个定理是沟通函数极限和数列极限的桥梁，通常用来证明某些函数极限不存在

例 21. (例1.3.18) 证明：当$x\to 0$时，$f(x)=\sin\frac1x$的极限不存在

例 22. 证明：当$x\to+\infty$时，$f(x)=\cos(x)$的极限不存在

例 23. 证明：Dirichlet函数

\[D(x)=\left\{\begin{aligned} 1, x\in \mathbb{Q} \\ 0, x\notin \mathbb{Q} \end{aligned}\right. \]

在任意一点的极限不存在。

函数极限存在的判别法

定理 9. (函数极限的两边夹定理)
当$x\to x_0$时，有$g(x)\to l$, $h(x)\to l$。且在$x_0$附近有

\[g(x)\leq f(x)\leq h(x) \]

则有

\[\lim_{x\to x_0}f(x)=l \]

例 24. 求极限$\displaystyle\lim_{x\to 0+}x[\frac1x]$

例 25. 求极限$\displaystyle\lim_{x\to0}\cos(x)=1$

定理 10. (函数极限的单调有界判别法)
设$f(x)$在$(a,b)$中单调有界，则$f(a+)$, $f(b-)$存在。

定理 11.
单调有界函数在其区间上每一点都有左、右极限。进一步地，如果$f(x)$在$(a,b)$内单调增，则有

\[f(x_0-)\leq f(x_0)\leq f(x_0+) \]

如果$f(x)$在$(a,b)$内单调减，则有

\[f(x_0-)\geq f(x_0)\geq f(x_0+) \]

定理 12. (Cauchy收敛准则)
设函数$f(x)$在$x_0$的某个去心邻域内有定义，则$f(x)$在点$x_0$处有极限的充要条件是， $\forall \epsilon>0$, $\exists \delta>0$, 满足

\[\begin{aligned} |f(x')-f(x'')|<\epsilon, \forall & 0<|x'-x_0|<\delta, \\ & 0<|x''-x_0|<\delta \end{aligned} \]

注. Cauchy准则通常用来判别某个极限不存在

如何描述非Cauchy收敛？并证明$x\to0$时，$\sin\frac1x$的极限不存在。

两个重要的的极限及其应用

命题 2.
$\displaystyle\lim_{x\to 0}\frac{\sin x}x=1$

命题 3.
$\displaystyle\lim_{x\to \infty}\left(1+\frac1x\right)^{x}=e$

$\displaystyle\lim_{x\to 0}(1+x)^{\frac1x}=e$

利用数列极限与函数极限的关系，可以有如下结论：

  1. 若$\lim a_n=0$，则有
    \[\lim_{n\to+\infty} \frac{\sin(a_n)}{a_n}=1 , \lim_{n\to+\infty} (1+a_n)^{\frac1{a_n}}=e \]
  2. 若$\lim a_n=\infty$，则
    \[\lim_{n\to+\infty} \left(1+\frac1{a_n}\right)^{a_n}=e \]

例 26. $\displaystyle\lim_{x\to 0}\frac{\sin 5x}x$

例 27. $\displaystyle\lim_{x\to 0}\frac{1-\cos x}{x^2}$

例 28. $\displaystyle\lim_{x\to a}\frac{\sin x-\sin a}{x-a}$

例 29. $\displaystyle\lim_{x\to 0}\frac{\ln(1+x)}{x}$

例 30. 求$\displaystyle\lim_{x\to 0}\frac{e^x-1}{x}$ , $\displaystyle\lim_{x\to 0}\frac{a^x-1}{x}$ , 其中$a>0$

例 31. 对于$a>0$，求$\displaystyle\lim_{x\to 0}\frac{(1+x)^a-1}{x}$

例 32. $\displaystyle\lim_{x\to +\infty}\left(\frac{x^2+1}{x^2-1}\right)^{x^2}$

例 33. $\displaystyle\lim_{n\to +\infty}\left(1+\frac{x}n\right)^{n}$

若$\displaystyle\lim_{x\to a}f(x)=1$, $\displaystyle\lim_{x\to a}g(x)=\infty$，则$\displaystyle\lim_{x\to a}f(x)^{g(x)}$也是一种未定式，称为$1^{\infty}$型未定式。

\[\begin{aligned} \lim_{x\to a}f(x)^{g(x)} = & \lim_{x\to a}(1+f(x)-1)^{g(x)} \\ =&\lim_{x\to a}\left[\left(1+f(x)-1\right)^{\frac1{f(x)-1}}\right]^{(f(x)-1)g(x)} \end{aligned} \]

若$\displaystyle\lim_{x\to a}(f(x)-1)g(x)=B$，则$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^B$ ($B$也可以是$\pm\infty$)

例 34. 求$\displaystyle\lim_{x\to+\infty}\left(\sin\frac1x+\cos\frac1x\right)^x$

无穷大量与无穷小量

定义 8. (无穷大量)
函数$f(x)$在$x_0$附近有定义，若对任意$M>0$，$\exists\delta>0$，满足

\[|f(x)|>M , \forall 0<|x-x_0|<\delta \]

则称$x\to x_0$时，$f(x)$为无穷大量,记为

\[\lim_{x\to x_0}f(x)=\infty \]

类似，可以定义$\displaystyle\lim_{x\to x_0}f(x)=+\infty$, $\displaystyle\lim_{x\to x_0}f(x)=-\infty$,$\displaystyle\lim_{x\to x_0-}f(x)=\infty$, $\displaystyle\lim_{x\to x_0+}f(x)=\infty$,$\displaystyle\lim_{x\to +\infty}f(x)=\infty$, $\displaystyle\lim_{x\to +\infty}f(x)=+\infty$, $\displaystyle\lim_{x\to +\infty}f(x)=-\infty$, $\cdots$ 等情形

  1. 在同一个极限过程中，两个无穷大量的积还是无穷大量。
  2. 两个无穷大量的和、差、商的性态具有各种可能，因此分别称为$\infty\pm\infty$型和$\frac{\infty}{\infty}$型未定式。

定义 9.
设$f(x)$在$x_0$附近有定义，若$\displaystyle\lim_{x\to x_0}f(x)=0$，则称$f(x)$是当$x\to x_0$时的无穷小量。

  1. 有限个无穷小量的和仍然是无穷小量，有限个无穷小量的积仍然是无穷小量。
  2. 一个有界变量与无穷小量的乘积仍然是无穷小量。
  3. 两个无穷小量的商有各种不同的性态，称为$\frac{0}0$型未定式。
  1. 若$u(x)$是无穷大量，则$\frac1{u(x)}$是无穷小量。
  2. 若$u(x)$是无穷小量，且$u(x)\neq0$，则$\frac1{u(x)}$是无穷大量。

定义 10. (无穷大量的比较)
设在同一变化中（以$x\to x_0$为例），变量$\alpha(x)$和$\beta(x)$都是无穷大量，

（1） 如果极限$\displaystyle\lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=A\neq 0$，则称$x\to x_0$时，$\alpha(x)$和$\beta(x)$是同阶无穷大量。如果$A=1$，则称$x\to x_0$时，$\alpha(x)$和$\beta(x)$是等价无穷大量，记为

\[\alpha(x) \sim \beta(x) , x\to x_0 \]

（2） 如果极限$\displaystyle\lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=0$，则称$x\to x_0$时，$\beta(x)$是比$\alpha(x)$更高阶的无穷大量，记为

\[\alpha(x)=o(\beta(x)) , x\to x_0 \]

例 35. $x^2+3x+5 \sim x^2 (x\to\infty)$

例 36. $\ln x=o(x), x\to+\infty$

定义 11. (无穷小量的比较)
设同一变化过程中（以$x\to x_0$为例），变量$\alpha(x)$和$\beta(x)$都是无穷小量，并且$\beta(x)\neq 0$。

（1） 如果$\displaystyle\lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=A\neq 0$为一有限数，则称$\alpha(x)$与$\beta(x)$是同阶无穷小量。 若$A=1$，则称$\alpha(x)$和$\beta(x)$是等价无穷小，记为

\[\alpha(x) \sim \beta(x) , x\to x_0 \]

（2）如果$\displaystyle\lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=0$，则称$\alpha(x)$是比$\beta(x)$更高阶的无穷小量，记为

\[\alpha(x)=o(\beta(x)), x\to x_0 \]

$\alpha(x)=o(1), x\to x_0$，就可以表示$\displaystyle\lim_{x\to x_0}\alpha(x)=0$

例 37. 当$x\to 0$时，有

$\sin(x) \sim x, x\to 0$ , $ \tan x \sim x, x\to 0$

$ \arctan x \sim x, x\to 0$

$1-\cos x \sim \frac{x^2}2 , x\to 0$

$\sqrt[n]{1+x}-1 \sim \frac{x}n , x\to 0$

等价无穷小有如下特性：

  1. $\phi(x) \sim \phi(x)$
  2. 若$\phi(x) \sim \psi(x)$, 则$\psi(x) \sim \phi(x)$
  3. 若$\phi(x) \sim \psi(x)$, $\psi(x) \sim \chi(x)$，则$\phi(x) \sim \chi(x)$

定理 13. (等价无穷小量代换)
$x\to x_0$时，$\alpha(x)$, $\beta(x)$, $\alpha_1(x)$, $\beta_1(x)$都是无穷小量，且$\alpha(x)\sim\alpha_1(x)$, $\beta(x)\sim\beta_1(x)$，如果$\displaystyle\lim_{x\to x_0}\frac{\alpha_1(x)}{\beta_1(x)}$存在，则有

\[\lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=\lim_{x\to x_0}\frac{\alpha_1(x)}{\beta_1(x)} \]
  1. 定理表明，在求极限过程中，可以用一个等价无穷小量替换乘除运算中整个式子的一个无穷小量。
  2. 无穷大量也可以实行等价替换。

例 38. $\displaystyle\lim_{x\to 0}\frac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{x^3}$

例 39. $\displaystyle\lim_{x\to 0} \frac{\sin x-\tan x}{x^3}$

例 40. $\displaystyle\lim_{x\to 0}(\cos x)^{\frac1{x\sin x}}$

例 41. $\displaystyle\lim_{x\to 0}\left(\frac{\sin x}{\tan x}\right)^{\frac1{\tan^2x}}$

例 42. 求$\displaystyle\lim_{x\to 0}\left[1+\ln(1+x)\right]^{\frac2x}$

关于$O$与$o$符号，有

  1. 若$x_0$附近，比值$\frac{f(x)}{g(x)}$有界，即存在$c>0$，满足 $|\frac{f(x)}{g(x)}|\leq c$，就记
    \[f(x)=O(g(x)), x\to x_0 \]
    特别，$f(x)=O(1)$表示$f(x)$有界。
  2. 如果
    \[\lim_{x\to x_0}\frac{f(x)}{g(x)}=0 \]
    则记
    \[f(x)=o(g(x)), x\to x_0 \]

例 43. $\displaystyle x-\sin(x) = O(x^3) , x\to 0$

谢谢

vertical slide 2

目录

本节读完

例 44. 求$\displaystyle\lim_{x\to+\infty}(\sqrt{x+\sqrt{x+\sqrt x}}-\sqrt x)$

例 45. 求$\displaystyle\lim_{x\to1}\frac{(1-\sqrt x)(1-\sqrt[3]x)\cdots(1-\sqrt[n]x)}{(1-x)^{n-1}}$

例 46. 求$\displaystyle\lim_{x\to+\infty}(\sin(x+1)-\sin x)$

44.