2. 微分

单变量函数的微分学

张瑞
中国科学技术大学数学科学学院

微分

微分的定义

定义 1. (可微)
设$y=f(x)$在$I$的邻域内有定义，$x_0,x_0+\Delta x$在$I$内，$\Delta y=f(x_0+\Delta x)-f(x_0)$为函数的增量，若

\[\Delta y=A\Delta x+o(\Delta x), \Delta x\to0 \]

即，

\[\lim_{\Delta x\to0}\dfrac{\Delta y-A\Delta x}{\Delta x}=0 \]

其中$A$是不依赖$\Delta x$的数。则称$f(x)$在$x_0$处可微，而$A\Delta x$为函数$f(x)$的在$x_0$处的微分，记为$dy$，即

\[dy=A\Delta x , \ \ \ \mbox{or}\ \ \ df=A\Delta x \]

定理 1.
$f(x)$在$x_0$处可微，当且仅当$f(x)$在$x_0$可导，且

\[dy=f'(x_0)\Delta x \]
  1. 函数$y=f(x)$在点$x$处的微分是一个将$\Delta x$映射到$f'(x)\Delta x$的函数
  2. 对于特别的函数$y=x$的微分为$dx=(x)'\Delta x=\Delta x$。因此，对于一般函数$y=f(x)$的微分，常常记为
    \[dy=d f(x)=f'(x)\Delta x=f'(x) dx \]
  3. 对于一元函数，可微与可导等价。

对于$\frac{dy}{dx}$，

  • 即可以看作是一个完整的符号，表示微商（或导数）；
  • 也可以看作是两个微分的商
    \[\frac{dy}{dx}=\frac{f'(x)dx}{dx}=f'(x) \]

导数：强调的是变化率，

微分：强调的是从$\Delta y$中，取出$\Delta x$的线性部分

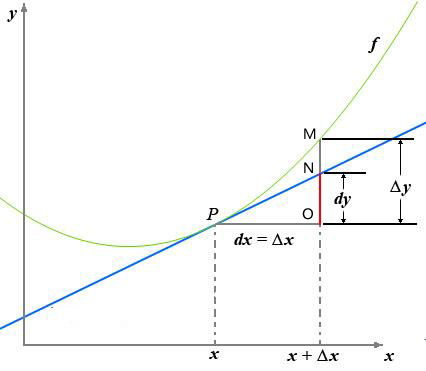
chap3-diff-diff

微分的运算与一阶微分形式的不变性

$d(\sin(x))=\cos(x)dx$, $d(\cos(x))=-\sin(x)dx$,
$d(\tan(x))=\sec^2(x)dx=\dfrac{dx}{\cos^2(x)}$ $d(\cot(x))=\dfrac{-dx}{\sin^2(x)}$
$d(\arcsin(x))=\dfrac{1}{\sqrt{1-x^2}}dx$ $d(\arccos(x))=\dfrac{-1}{\sqrt{1-x^2}}dx$
$d(\arctan(x))=\dfrac{1}{1-x^2}dx$
$d(e^x)=e^xdx$, $d(a^x)=a^x \ln adx$,
$d(\ln(\|x\|))=\dfrac{1}{x}dx$, $d(\log_a x)=\dfrac{1}{x\ln a}dx$
$d(x^\mu)=\mu x^{\mu-1}dx$
\[\begin{aligned} d(\sinh(x))&=d\left(\frac{e^x-e^{-x}}2\right)=\frac{e^x+e^{-x}}2dx=\cosh(x)dx , \\ d(\cosh(x))&=\sinh(x)dx \\ d(\tanh(x))&=\displaystyle\frac1{\cosh^2(x)}dx \\ d(\mbox{arcsinh}(x))&=d(\ln(x+\sqrt{1+x^2}))=\dfrac{1}{\sqrt{1+x^2}}dx \\ d(\mbox{arccosh}(x))&=d(\ln(x+\sqrt{x^2-1}))=\dfrac{1}{\sqrt{x^2-1}}dx \\ d(\mbox{arctanh}(x))&=d\left(\frac12 \ln\dfrac{1+x}{1-x}\right)=\dfrac{1}{1-x^2}dx \end{aligned} \]

定理 2. (微分的四则运算)
$u(x)$,$v(x)$可微，则有

\[d(Cu)=Cdu, C \mbox{ is const} \]
\[d(u\pm v)=du\pm dv \]
\[d(uv)=u'dv+v'du \]
\[d(\dfrac{u}{v})=\dfrac{vdu-udv}{v^2} , v\neq 0 \]

定理 3. (复合函数微分)
$y=f(u),u=\phi(x)$可微，则$f(\phi(x))$可微，且

\[d(f(\phi(x)))=(f(\phi(x)))'dx=f'(\phi(x))\phi'(x)dx \]

由$u=\phi(x)$，则$du=\phi'(x)dx$，所以，上式又可以写成

\[\begin{aligned} d(f(u))=&d(f(\phi(x)))=f'(\phi(x))\phi'(x)dx \\ =&f'(u)\phi'(x)dx=f'(u)du \end{aligned} \]

称为，一阶微分形式的不变性

若$y=f(u)$, $u=u(x)$, $x=x(t)$，则有

  1. $dy=f'(u)du=f'(u)u'(x)dx=f'(u)u'(x)x'(t)dt$
  2. $\displaystyle\frac{dy}{dt}=\frac{dy}{du}\frac{du}{dx}\frac{dx}{dt}$

例 1. 求$f(x)$的微分，其中

\[f(x)=\ln(x+\sqrt{1+x^2}) \]

例 2. $u,v$是$x$的可微函数，求$y=\arctan\dfrac{u}{v}$的微分

例 3. 求$\dfrac{d}{d(x^3)}(x^3-2x^6-x^9)$

例 4. (例3.2.3) 设$0<q<1$，函数$y(x)$满足

\[y-x-q\sin(y)=0 \]

求$y(x)$的导数。

谢谢

vertical slide 2

目录

本节读完

例 5. 谢

5.