|
张瑞
中国科学技术大学数学科学学院
rui@ustc.edu.cn |
- 若空间中动点的坐标满足一般的三元方程,则动点的自由度为2,动点就限制在一张曲面上。
- 若空间中动点满足两个方程, ,则动点就在一条曲线上。
把满足方程
的点构成的图像看成是空间中的一张曲面,称为方程所表示的隐式曲面。
同理,
代表的是空间中一条曲线,也称为隐式曲线。
以二次方程表示的曲面,也称为二次曲面。
柱面
定义 1.
一簇平行直线形成的曲面叫柱面。直线叫母线。与每条母线都相交的线叫准线。
准线有无穷条,将任一条准线沿母线方向运动,都可以得到柱面
母线与轴平行的柱面方程是
同样,方程表示母线与轴平行。方程表示母线与轴平行。
注.
这里,在空间中考虑问题。虽然方程中不含变量,但方程是关于的三元方程。
常见的母线平行轴的二次柱面
- 圆柱面
- 椭圆柱面
- 双曲柱面
- 抛物柱面
旋转面
定义 2.
一条曲线绕一条直线旋转产生的曲面叫作旋转面。这条曲线称为子午线,这条直线称为转轴。
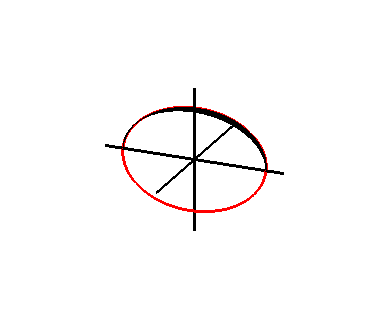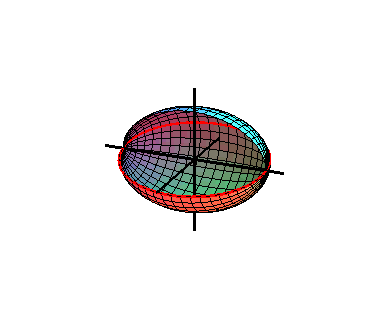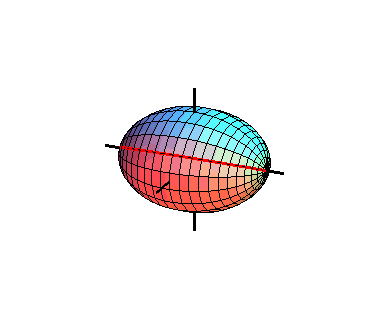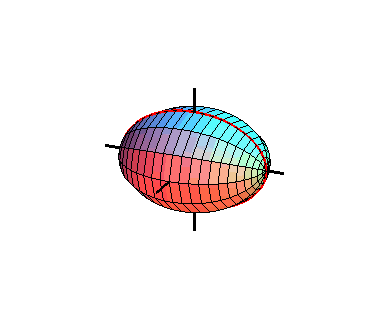
例 1. 平面上的椭圆
绕轴旋转,所得的曲面称为旋转椭球面。
这个椭球上任意点,
- 它在过这个点,并且与轴垂直的圆上,这个圆的圆心在轴,半径是
- 是椭圆上的点绕轴旋转得到,因此有
推广到一般情况,设在平面上有曲线
- 绕轴旋转得到一个旋转面,则旋转面的方程为
这里的表示至少有一种情况成立。
- 类似,绕轴旋转,得到的旋转面的方程是
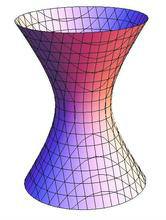
例 2. (例8.3.1) 设是平面上的双曲线
则绕轴旋转所得的称为旋转单叶双曲面,方程是
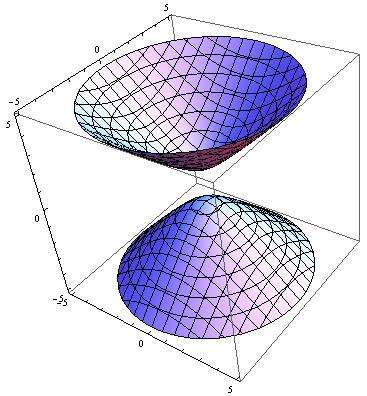
绕轴旋转所得的称为旋转双叶双曲面,方程是
|
|
例 3. (例8.3.2) 平面上的抛物线
绕轴旋转得到旋转抛物面,方程是
例 4. (例8.3.3) 平面上的直线
绕轴旋转得到圆锥面,方程是
椭球面
椭球面的方程是
椭球面的一个特点是,它与平面, 相截,截口是一个椭圆,
在椭球面方程中,若, , 中有两个相等,得到的是旋转椭球面。
若,得到球面方程
双曲面
方程
定义的曲面称为单叶双曲面(uniparted hyperboloid)。
它与平面的截口是一个椭圆
它与平面(或)的截口是双曲线
当时,方程退化为两条直线
方程
定义的曲面称为双叶双曲面(biparted hyperboloid)。
它与平面(要求)的截口是一个椭圆,
它与平面(或)的截口是双曲线
当时,方程是一个双叶旋转双曲面。
二次锥面
方程
所表示的曲面称为二次锥面。
易知,若在锥面上,则直线
均在锥面上。
锥面是由一系列通过定点的直线所构成。这个定点,称为顶点,构成锥面的直线称为母线。
用平行于坐标面的平面得到的截口为一个椭圆
平面或得到的截口是双曲线。
若,干净锥面是一个圆锥面
椭圆抛物面
方程
定义的曲面称为椭圆抛物面(Elliptic paraboloid)。
平面()得到的截口是一个椭圆,
平面和得到的截口均是抛物线。
双曲抛物面
方程
定义的曲面称为双曲抛物面,它的形状像马鞍,也称为马鞍面。
平面的截口方程是
- 当时,曲线是双曲线,实轴平行与轴,虚轴平行于轴。
- 当时,曲线是双曲线,实轴平行与轴,虚轴平行于轴。
- 当时,是两个相交于原点的直线。
平面的截口方程是
是一条开口指向轴反方向的抛物线。
平面的截口方程是
是一条开口指向轴方向的抛物线。
一个一般的三元二次方程
可以通过坐标的平移和旋转, 化为上述的几种类型或他们的退化形态。
|
在曲线上取两点和,其横坐标分别为与,
则两点的距离为 |