4. 坐标变换与其它常用坐标系

空间解析几何

张瑞
中国科学技术大学数学科学学院

坐标变换与其它常用坐标系

坐标变换

空间中，两个不同的右手直角坐标系，其中一个可以通过平移与旋转与另一个重合。

设$F=[O;\vec i, \vec j, \vec k]$和$F'=[O';\vec i', \vec j', \vec k']$是 空间中两个不同的右手直角坐标系。点$P$在两个坐标系下的坐标分别是$(x,y,z)$和$(x',y',z')$。 下面，来看两个坐标之间的关系。

平移

设$F$和$F'$的坐标系坐标轴方向相同，原点不同，即$O'\neq O$, $\vec i'=\vec i$, $\vec j'=\vec j$, $\vec k'=\vec k$。 且有

\[\overrightarrow{OP}=x\vec i+y\vec j+z\vec k, \quad \overrightarrow{O'P}=x'\vec i+y'\vec j+z'\vec k \]

注意到$\overrightarrow{O'P}=\overrightarrow{OP}-\overrightarrow{OO'}$，

  • 并设$\overrightarrow{OO'}=a\vec i+b\vec j+c\vec k$（即$O'$在坐标系$F$下的坐标是$(a,b,c)$，则有
    \[x'\vec i+y'\vec j+z'\vec k=(x-a)\vec i+(y-b)\vec j+(z-c)\vec k \]
  • 因此，得到平移时的坐标变换公式
    \[x'=x-a, \quad y'=y-b, \quad z'=z-c \]

例 1. (例8.4.1) 下面方程刻划的是什么图形

\[4x^2+25y^2+4z^2-16x-50y-16z-43=0 \]

解. 配方，原方程变为

\[4(x-2)^2+25(y-1)^2+4(z-2)^2-100=0 \]

将坐标原点平移到$(2,1,2)$，即取

\[x'=x-2, y'=y-1, z'=z-2 \]

代入得到

\[\frac{x'^2}{5^2}+\frac{y'^2}{2^2}+\frac{z'^2}{5^2}=1 \]

是个（旋转）椭球面。

旋转

设两个右手直角坐标系$F$和$F'$的原点相同，但坐标轴方向不同。 设两个坐标系的基向量$\{\vec i, \vec j,\vec k\}$和$\{\vec i', \vec j',\vec k'\}$ 之间的夹角为

$\vec i$ $\vec j$ $\vec k$
$\vec i'$ $\alpha_1$ $\beta_1$ $\gamma_1$
$\vec j'$ $\alpha_2$ $\beta_2$ $\gamma_2$
$\vec k'$ $\alpha_3$ $\beta_3$ $\gamma_3$

利用方向余弦表示，知道

\[\begin{aligned} \vec i'=\cos(\alpha_1)\vec i+\cos(\beta_1)\vec j+\cos(\gamma_1)\vec k \\ \vec j'=\cos(\alpha_2)\vec i+\cos(\beta_2)\vec j+\cos(\gamma_2)\vec k \\ \vec k'=\cos(\alpha_3)\vec i+\cos(\beta_3)\vec j+\cos(\gamma_3)\vec k \\ \end{aligned} \]

又$\vec i'$, $\vec j'$, $\vec k'$两两正交，因此有

\[\cos(\alpha_i)\cos(\alpha_j)+\cos(\beta_i)\cos(\beta_j) +\cos(\gamma_i)\cos(\gamma_j)=\delta_{ij} \]

点$P$在两个坐标系下的坐标分别是$(x,y,z)$和$(x',y',z')$，则有

\[\begin{aligned} \overrightarrow{OP}=&x\vec i+y\vec j+z\vec k \\ =&x'\vec i'+y'\vec j'+z'\vec k' \\ =&x'(\cos(\alpha_1)\vec i+\cos(\beta_1)\vec j+\cos(\gamma_1)\vec k) \\ & + y'(\cos(\alpha_2)\vec i+\cos(\beta_2)\vec j+\cos(\gamma_2)\vec k) \\ & + z'(\cos(\alpha_3)\vec i+\cos(\beta_3)\vec j+\cos(\gamma_3)\vec k) \\ =&(x'\cos(\alpha_1)+y'\cos(\alpha_2)+z'\cos(\alpha_3))\vec i \\ &+(x'\cos(\beta_1)+y'\cos(\beta_2)+z'\cos(\beta_3))\vec j \\ &+(x'\cos(\gamma_1)+y'\cos(\gamma_2)+z'\cos(\gamma_3))\vec k \\ \end{aligned} \]

由线性代数的知识，存在正交阵$A=(a_{ij})$，成立

\[\begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} =A \begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} \]

若点$P$在两个坐标系下的坐标分别是$(x,y,z)$和$(x',y',z')$，则有

\[\begin{aligned} \overrightarrow{OP}=&\begin{pmatrix} x & y & z\end{pmatrix}\begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} =\begin{pmatrix} x' & y' & z'\end{pmatrix}\begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} \\ =&\begin{pmatrix} x' & y' & z'\end{pmatrix}A \begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} \end{aligned} \]

得到旋转坐标变换公式：

\[\begin{aligned} x= & x'\cos(\alpha_1)+y'\cos(\alpha_2)+z'\cos(\alpha_3) \\ y= & x'\cos(\beta_1)+y'\cos(\beta_2)+z'\cos(\beta_3) \\ z= & x'\cos(\gamma_1)+y'\cos(\gamma_2)+z'\cos(\gamma_3) \\ \end{aligned} \]

同样，有

\[\begin{aligned} x'= & x\cos(\alpha_1)+y\cos(\beta_1)+z\cos(\gamma_1) \\ y'= & x\cos(\alpha_2)+y\cos(\beta_2)+z\cos(\gamma_2) \\ z'= & x\cos(\alpha_3)+y\cos(\beta_3)+z\cos(\gamma_3) \\ \end{aligned} \]

由$A$正交，因此

\[\begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} =A^{T} \begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} \]

则有

\[\begin{aligned} \overrightarrow{OP}=&\begin{pmatrix} x & y & z\end{pmatrix}\begin{pmatrix} \vec i \\ \vec j \\ \vec k \end{pmatrix} =\begin{pmatrix} x' & y' & z'\end{pmatrix}\begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} \\ =&\begin{pmatrix} x & y & z\end{pmatrix}A^T \begin{pmatrix} \vec i' \\ \vec j' \\ \vec k' \end{pmatrix} \end{aligned} \]

当一个轴不动时（如$z$轴不动），则有

$\vec i$ $\vec j$ $\vec k$
$\vec i'$ $\alpha$ $\frac{\pi}2-\alpha$ $\frac{\pi}2$
$\vec j'$ $\frac{\pi}2+\alpha$ $\alpha$ $\frac{\pi}2$
$\vec k'$ $\frac{\pi}2$ $\frac{\pi}2$ $0$

坐标转换公式为

\[\begin{aligned} x=&x'\cos(\alpha)-y'\sin(\alpha) \\ y=&x'\sin(\alpha)+y'\cos(alpha) \\ z=&z' \end{aligned} \]

例 2. (例8.4.2) 将直角坐标系$Oxyz$绕$z$轴逆时针旋转$\frac{\pi}4$后，得到新坐标系$Ox'y'z'$。 试表示新旧坐标间的变换关系，并给出方程$xy=z$在新坐标系下的表达式

解. 依题意，有

\[\begin{aligned} x=&x'\cos(\frac{\pi}4)-y'\sin(\frac{\pi}4)=\frac{\sqrt 2}2(x'-y') \\ y=&x'\sin(\frac{\pi}4)+y'\cos(\frac{\pi}4)=\frac{\sqrt 2}2(x'+y') \\ z=&z' \end{aligned} \]

代入方程后，得到 $\frac{\sqrt 2}2(x'-y')\frac{\sqrt 2}2(x'+y')=z'$，

即有 $\displaystyle\frac{x'^2}2-\frac{y'^2}2=z'$ 是一个马鞍面。

例 3. (例8.4.3) 利用坐标变换化简方程

\[45x^2+45y^2-8z^2-54xy +36\sqrt 2 x-108\sqrt2 y+32z+184=0 \]

并指出它是什么曲面。

其它常用坐标系

前面介绍的坐标系，是由一个原点和三个不共面的向量组成。这样的空间坐标系是线性坐标系， 它的一个坐标分量等于常量所对应的面都是平面。

下面介绍一些常见的非线性坐标系。

平面的极坐标系

在平面上取定一点$O$(称为极点)，从极点引一条射线$Ox$(称为极轴)， 再选定一个长度单位和角度的正向(通常取逆时针方向为正)，这样就构成的平面上的极坐标系。

对于平面上任意一点$P$，用$r$表示$P$到$O$的距离(线段$OP$的长度，或向量$\overrightarrow{OP}$的长度)，$\theta$表示从极轴到向量$\overrightarrow{OP}$的正向夹角(称为辐角)， 则数组$(r, \theta)$可以确定点$P$在空间的位置，并称为点$P$的极坐标。

$r$的取值范围是$[0,+\infty)$，$\theta$的取值范围是$[0,2\pi)$。

在直角坐标$[O;\vec i, \vec j ]$中，取$O$为极点，$x$轴为极轴。 则平面上任意一点$P$的直角坐标$(x,y)$和极坐标$(r,\theta)$的变换关系为

\[\begin{cases} x=r\cos\theta \\ y=r\sin\theta \end{cases}, \quad \begin{cases} r=\sqrt{x^2+y^2} \\ \theta=\arctan\frac{y}x \end{cases} \]

$P$的位置向量可以表示为

\[\vec r=x\vec i+y\vec j=r\cos\theta\vec i+r\sin\theta\vec j \]

注. 可以发现，$r$为常数是平面上以$O$为圆心的圆， $\theta$为常数是从$O$出发的射线。

柱坐标系

在空间坐标系$[O;\vec i, \vec j, \vec k]$中，将$Oxy$平面坐标换成极坐标。 即空间中点$P(x,y,z)$用坐标$P(r, \theta, z)$来表示，其中

\[x=r\cos\theta, \quad y=r\sin\theta, \quad z=z \]

其中$r\geq 0$, $\theta\in[0,2\pi)$, $z\in\mathbb{R}$。 这样给出了空间的柱坐标系。 $(r, \theta, z)$称为点$P$的柱坐标。

注. 在柱坐标中，$r=c$表示一个圆柱面，$\theta=\theta_0$表示以$z$轴为边的半平面。

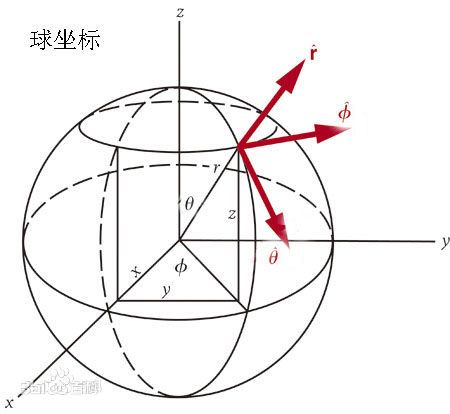
球坐标系

设位置向量$\overrightarrow{OP}$与$z$轴的夹角为$\theta$， $\overrightarrow{OP}$在$Oxy$平面上的投影向量是$\overrightarrow{OP_1}$， 则有

\[z=|OP|\cos\theta, \quad \vec r=\overrightarrow{OP}=\overrightarrow{OP_1}+|OP|\cos\theta\vec k \]

将$P_1$用$xy$平面的极坐标来表示，设辐角是$\phi$，则有

\[\overrightarrow{OP_1}=|OP_1|\cos\phi\vec i+|OP_1|\sin\phi\vec j \]

记$r=|OP|=|\vec r|$，则$|OP_1|=r\sin\theta$，从而有

\[\vec r=r\sin\theta\cos\phi\vec i+r\sin\theta\sin\phi\vec j+r\cos\theta\vec k \]

即有

\[x=r\sin\theta\cos\phi, y=r\sin\theta\sin\phi, z=r\cos\theta \]

其中$r\geq 0$, $\theta\in[0,\pi]$, $\phi\in[0,2\pi)$。 称$(r,\theta,\phi)$为$P$的球坐标，形成的坐标系是球坐标系。

ball-coordinate

谢谢

http://www.360doc.com/content/18/0421/08/54440535_747456429.shtml

在曲线上取两点$M$和$M'$，其横坐标分别为$x$与$x+dx$， 则两点的距离为

目录

本节读完

例 4. 谢

4.