7. 统计回归模型(III)

数学建模

张瑞
中国科学技术大学数学科学学院

统计回归模型

主成分分析

例 1. 某高校对报名推荐免试研究生的52名学生的6门课程的考试分数统计如下。其中数学分析、高等代数、概率论闭卷，微分几何、抽象代数、数值分析开卷。如何最大程度地区分学生的考试成绩，在评价中体现开卷、闭卷的影响，给出合理的成绩排序

学生 数学分析 高等代数 概率论 微分几何 抽象代数 数值分析 总分
A1 62 71 64 75 70 68 410
A2 52 65 57 67 60 58 359
… …
A52 70 73 70 88 79 69 449
  • 主成分分析（Principal Component Analysis，PCA）和因子分析(Factor Analysis)是解决这个问题的两种方法

主成分分析(principal component analysis)是1901年Pearson对非随机变量引入的,1933年Hotelling将此方法推广到随机向量的情形。

  • 主成分分析的主要目的是希望用较少的变量去解释原来资料中的大部分变异,将许多相关性很高的变量转化成彼此相互独立或不相关的变量。
  • 通常是选出比原始变量个数少,能解释大部分资料中的变异的几个新变量,即所谓主成分,并用以解释资料的综合性指标。
  • 由此可见,主成分分析实际上是一种降维方法。

如果用 $x_1$ , $x_2$ , $\cdots$ , $x_p$ 表示 $p$ 门课程, $c_1$ , $c_2$ ,$\cdots$, $c_p$ 表示各门课程的权重,那么加权之和就是

\[s = c_1 x_1 + c_2 x_2 + \cdots + c_p x_p \]
  • 每个学生都对应一个这样的综合成绩,记为 $s_1$ , $s_2$ , $\cdots$ , $s_n$ , $n$ 为学生人数。
  • 我们希望选择适当的权重能更好地区分学生的成绩。即是说,需要寻找这样的加权,能使 $s_1$ , $s_2$ , $\cdots$ , $s_n$ 尽可能的分散

设 $X_1$ , $X_2$ , $\cdots$ , $X_p$ 表示以 $x_1$ , $x_2$ , $\cdots$ , $x_p$ 为样本观测值的随机变量,如果能找到$c_1$ , $c_2$ ,$\cdots$, $c_p$,使得

\[Var ( c_1 X_1 + c_2 X_2 + \cdots + c_p X_p ) \]

的值达到最大,同时限制$c_1^2 + c_2^2 + \cdots + c^2_p = 1$。则由于方差反映了数据差异的程度,因此也就表明我们抓住了这 $p$ 个变量的最大变异。由于这个解是 $p −$ 维空间的一个单位向量,它代表一个“方向”,它就是常说的主成分方向。

  • 一个主成分不足以代表原来的 $p$ 个变量,因此需要寻找第二个乃至第三、第四主成分,
  • 第二个主成分不应该再包含第一个主成分的信息,统计上的描述就是让这两个主成分的协方差为零,几何上就是这两个主成分的方向正交。

设 $Z_ i$ 表示第 $i$ 个主成分, $i = 1 , 2 , \cdots , p$ ,可设

\[\begin{cases} Z_1 = c_{11} X_ 1 + c_{12} X_ 2 + \cdots + c_{1p} X_ p=\vec c_1^T\vec X \\ Z_2 = c_{21} X_ 1 + c_{22} X_ 2 + \cdots + c_{2p} X_ p=\vec c_2^T\vec X \\ \cdots \\ Z_p = c_{p1} X_ 1 + c_{p2} X_ 2 + \cdots + c_{pp} X_ p=\vec c_p^T\vec X \\ \end{cases} \]
  • 其中对每一个 $i$ ,均有 $c_{i1}^2+ c_{i2}^2 + \cdots + c_{ip}^2 = 1$ ,
  • 且 $( c_{11} , c_{12} , \cdots , c_{1p} )$ 使得 $Var ( Z_ 1 )$ 的值达到最大;
  • $( c_{21} , c_{22} , \cdots , c_{2p} )$ 使得 $Var ( Z_ 2 )$ 的值达到最大，而且垂直于 $( c_{11} , c_{12} , \cdots , c_{1p} )$;
  • 以此类推可得全部$p$个主成分
  • 可以借助于计算机很容易完成

记$Z=(Z_1,Z_2,\cdots,Z_p)^T$，则前面式子可以简记为

\[Z=C \vec X, C=(c_{ij}) \]

因为$Z_1,\cdots,Z_p$互不相关，则协方差阵$Cov(Z)$为对角阵，记为$\Lambda=diag(\lambda_1,\cdots,\lambda_p)$。由

\[Cov(Z)=Cov(C\vec X)=C Cov(X) C^T=C\Sigma C^T=\Lambda \]

$\Sigma$为$X$的协方差阵，通常为对称正定的。则存在单位正交的特征向量$\vec c_1$, $\cdots$, $\vec c_p$，使得上式成立。

  • 也就是，$C$是$\Sigma$的特征向量组。
  • 取$\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_p\geq 0$，则对应的$Z_1$,$\cdots$,$Z_p$就是第一，$\cdots$，第p主成份。
  • 一般取$\sum_{i=1}^m\lambda_i\geq 80\%\sum_{i=1}^p\lambda_i$的前$m$个作为主成份降维使用。

给出学生$i$的第$j$门成绩$x_{ij}$。记$\vec x_{i}=(x_{i1},\cdots,x_{ip})^T$是$p$维随机变量$\vec X$的一个观测值，

  • 均值向量
    \[\vec{\bar x}=\frac1n\sum_{i=1}^n\vec x=(\bar x_1,\cdots,\bar x_p)^T \]
    作为$E(\vec x)=\vec \mu$的估计值，
  • $\vec X$的协方差矩阵
    \[S=\frac{1}{n-1}\sum_{i=1}^n(\vec x_i-\bar{\vec x})(\vec x_i-\bar{\vec x})^T \]
    作为$Cov(X)=\Sigma$的估计值。

学生成绩的特征值结果(statsmodels)

特征值 贡献率 累积贡献率
192.917105 0.618324 0.618324
65.542745 0.210073 0.828397
22.696618 0.072746 0.901143
14.343998 0.045974 0.947117
8.857153 0.028388 0.975505
7.642381 0.024495 1.000000 
import pandas as pd
import numpy as np
datascore=pd.read_excel("data/score0907.xlsx")
data=pd.DataFrame(datascore, columns=['数学分析',  '高等代数', '概率论',  '微分几何',  '抽象代数',  '数值分析'])
from statsmodels.multivariate.pca import PCA
res=PCA(data)
# 合并结果到数据集
for col in res.scores.columns:
    datascore[col]=res.scores[col]

percent=res.eigenvals/np.sum(res.eigenvals) # 贡献率
# 特征值， 贡献率， 累积贡献率
print("----:", np.array([res.eigenvals, percent, np.cumsum(percent)]).T)

主成份为

\[y_i=\sum_{j=1}^p c_{ij}(x_j-\bar x_j) \]

其中的主成份系数$c_{ij}$的值为 

数学分析      高等代数       概率论      微分几何      抽象代数      数值分析
comp_0  6.411144  5.837233  5.979237 -4.605889 -5.701651 -5.316647
单位化 [ 0.46158339  0.42026351  0.43048736 -0.33161035 -0.41050197 -0.38278283]
comp_1 -2.244423 -3.366099 -3.286718 -4.559566 -3.063579 -2.863042
单位化 [-0.27723143 -0.41578097 -0.4059758  -0.56319813 -0.37841365 -0.35364325]
  • 第一主成份对应闭卷系数为正，开卷系数为负，系数的绝对值相差不大。一个学生的开卷成绩高，数值为较大的正数；若闭卷成绩高，则为绝对值较大的负数。这个成份反映了开、闭卷的考试判别。
  • 第二主成份各个系数均为负数，且系数相差不大。表明了各科成绩的某种均衡性。
print("-------------Coeff: ",res.coeff)
comp0=res.coeff.loc['comp_0'].to_numpy()
print(comp0/np.sqrt(np.sum(comp0**2))) # 单位化处理
comp1=res.coeff.loc['comp_1'].to_numpy()
print(comp1/np.sqrt(np.sum(comp1**2))) # 单位化处理

mm7-ex-score-pca

  • 可以看到，A23, A24的第一主成份高，表明他们的闭卷考试成绩高；而A41, A3, A11的开卷考试成绩较高。
  • 在第二主成份上，A14,A25的各科成绩均衡，同时成绩也比较高（注意系数为负数），而A7,A12,A2的各科成绩均不理想。

用模块 sklearn 得到的结果

特征值： 

[460.64928625 170.60728235  57.38477937  28.69010096  21.00442058  15.82315415]

贡献率 

[0.61081187 0.22622189 0.07609109 0.03804251 0.02785145 0.02098119]

主成份系数 

 [ 5.15671820e-01  3.32074746e-01  3.87862955e-01 -4.53378702e-01  -3.45827091e-01 -3.84996935e-01]
 [ 3.81222011e-01  3.48212227e-01  4.14661747e-01  6.77007166e-01   2.22263365e-01  2.31805853e-01]
from sklearn.decomposition import PCA
X = data
pca = PCA()
pca.fit(X)

# 给出贡献率
print(pca.explained_variance_ratio_)  
# 特征值
print(pca.explained_variance_)  

# 各个主成份的系数
print(pca.components_)  

# 各个样本的主成份得分表
print(pca.transform(X))

因子分析

因子分析(factor analysis)是由英国心理学家Spearman在1904年提出来的,他成功地解决了智力测验得分的统计分析,长期以来,教育心理学家不断丰富、发展了因子分析理论和方法,并应用这一方法在行为科学领域进行了广泛的研究。

  • 因子分析是一种数据简化的技术。
  • 它通过研究众多变量之间的内部依赖关系,探求观测数据中的基本结构,并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。
  • 原始的变量是可观测的显在变量,而假想变量是不可观测的潜在变量,称为因子。

因子分析有确定的模型,观察数据在模型中被分解为公共因子、特殊因子和误差三部分。

  1. 主成分分析:原始变量的线性组合表示新的综合变量,即主成分。
  2. 因子分析:潜在的假想变量和随机影响变量的线性组合表示原始变量。

因子分析所涉及的计算与主成分分析很类似,但差别也是很明显的:

  1. 主成分分析把方差划分为不同的正交成分,而因子分析则把方差划归为不同的起因因子;
  2. 因子分析中特征值的计算只能从相关系数矩阵出发,且必须将主成分转换成因子。

因子分析是将原始变量$x_1$,$\cdots$,$x_p$分解为若干个因子的线性组合

\[\begin{cases} x_1=\mu_1+a_{11}f_1+\cdots+a_{1m}f_m+\epsilon_1 \\ x_2=\mu_2+a_{21}f_1+\cdots+a_{2m}f_m+\epsilon_2 \\ \cdots\\ x_p=\mu_1+a_{p1}f_1+\cdots+a_{pm}f_m+\epsilon_p \\ \end{cases} \]

简记为

\[\vec x=\vec \mu+A\vec f+\vec\epsilon \]

其中$\vec\mu$是$\vec x$的期望向量，$\vec f$称公共因子向量，$\vec\epsilon$称特殊因子向量，均为不可观测的向量，$A=(c_{ij})_{p\times m}$称为因子载荷矩阵。

假定：

  • $f_j$之间互不相关，且有单位方差
  • $\epsilon_i$互不相关，且与$f_j$互不相关，$Cov(\vec\epsilon)=\Phi$为对角阵

则有

\[Cov(\vec x)=AA^T+\Phi, \ \ \ Cov(\vec x,\vec f)=A \]

计算$A$的过程比较复杂，且这个矩阵不唯一。（只要$T$为$m$阶正交矩阵，则$AT$也是因子载荷矩阵）

分析模型：

学生数据的相关系数矩阵 

          数学分析      高等代数       概率论      微分几何      抽象代数      数值分析
数学分析  1.000000  0.813343  0.834741 -0.379514 -0.561244 -0.505401
高等代数  0.813343  1.000000  0.818799 -0.273686 -0.447372 -0.356803
概率论   0.834741  0.818799  1.000000 -0.243706 -0.438190 -0.461070
微分几何 -0.379514 -0.273686 -0.243706  1.000000  0.691559  0.573821
抽象代数 -0.561244 -0.447372 -0.438190  0.691559  1.000000  0.646317
数值分析 -0.505401 -0.356803 -0.461070  0.573821  0.646317  1.000000

从相关系数看，前3门课之间存在较强的正相关性，后3门课也存在正相关性 

特征值：  [3.70994432 1.26043741 0.43647343 0.14696887 0.17032986 0.27584611]
特征值贡献率%：  [61.83240537 21.00729016  7.27455719  2.4494811   2.83883096  4.59743521]

从特征值贡献率可以看到，前2个的占比超过80%。因此，认为公共因子个数$m=2$是合适的。 

data=pd.DataFrame(datascore, columns=['数学分析',  '高等代数', '概率论',  '微分几何',  '抽象代数',  '数值分析'])
# 相关系数矩阵
rr=data.corr() # pearson相关系数
print("相关系数矩阵： ")
print(rr)
eigenvalue,featurevector=np.linalg.eig(rr)
print("特征值： ",eigenvalue)
ee=eigenvalue/np.sum(eigenvalue)*100
print("特征值贡献率%： ",ee)

Python sklearn （期望最大化算法，EM算法） 得到的结果 

[[11.62807769  7.98559107  9.32759643 -6.63358709 -6.20826719 -6.58291325]
 [-1.20832196 -2.20086224 -2.72159962 -9.16961552 -5.18477723 -4.73066856]]
  • 第1个因子，前3项为正，后3项为负，可以看作是“开、闭卷因子”
  • 第2个因子，均为负数，后3项绝对值略大，可以看作“专业基础课因子” 
from sklearn.decomposition import FactorAnalysis

fa = FactorAnalysis(n_components=2) #n_components=7, random_state=0)
X=data
fa.fit(X)

print(fa.components_)

作图 

Xtrans=fa.transform(X)
datascore['factor0']=Xtrans[:,0]
datascore['factor1']=Xtrans[:,1]

from matplotlib import pyplot as plt
plt.scatter(datascore['factor0'],datascore['factor1'])
for i,row in datascore.iterrows(): #line in datascore.to_numpy():
    plt.text(row['factor0'],row['factor1'],row['学生序号'])
plt.show()

mm7-ex-score-sklearn

专业基础好：A14,A25,A13。成绩差： A7,A12,A2。 闭卷好：A23,A44。开卷好：A11,A3,A41

Python的statsmodels用缺省的主轴系数分析(principal axis factor analysis)，得到系数 

                           factor 0                       factor 1
------------------------------------------------------------------
数学分析                        -0.8873                         0.2581
高等代数                        -0.7943                         0.3864
概率论                         -0.8310                         0.4103
微分几何                         0.5905                         0.5573
抽象代数                         0.7590                         0.4370
数值分析                         0.6641                         0.3254
--------------------------------------------

第1个因子，“开、闭卷因子” 第2个因子，“平衡因子”， 结果与PCA类似。

from statsmodels.multivariate.factor import Factor
fa=Factor(data,n_factor=2) # 缺省是n_factor=1
res=fa.fit()
print(res.summary())

用Python statsmodels 的最大方差旋转法（Matlab缺省使用）得到 

载荷矩阵 (loading matrix)
[[-0.86249455 -0.33171513]
 [-0.86617931 -0.17324684]
 [-0.90983279 -0.17646775]
 [ 0.132707    0.80104387]
 [ 0.33957218  0.8073369 ]
 [ 0.33162977  0.66105646]]
  • 第1个因子，前3项绝对值明显比后3项大，可以看作“基础课因子”
  • 第2个因子，后3项绝对值明显比前3项大，可以看作“专业基础课因子” 
from statsmodels.multivariate.factor import Factor
fa=Factor(data,n_factor=2) # 缺省是n_factor=1
res=fa.fit()

res.rotate("varimax") # 最大方差旋转法（Matlab缺省使用）
print("载荷矩阵 (loading matrix)")
print(res.loadings) # loading matrix (载荷矩阵)

Xtrans=res.factor_scoring(X)

mm7-ex-score-statsmodels

专业基础好：A41,A14,A13。专业基础差： A7,A26,A17。 基础课好：A23,A44。基础课不好：A11,A2,A12

最终排名：以学生的2个因子得分作加权平均得到：

\[F(f_1,f_2)=\alpha_1f_1+\alpha_2f_2 \]

其中权值可以按心情设置，或按特征值占比计算，$\alpha_1=\frac{\lambda_1}{\lambda_1+\lambda_2}=0.746$， $\alpha_2=\frac{\lambda_2}{\lambda_1+\lambda_2}=0.253$

   学生序号  sk_num  sm_num  to_num
3    A4    17.0    11.0    18.0
5    A6    11.0    18.0    26.0
6    A7    46.0    50.0    52.0
8    A9     9.0    13.0    27.0
9   A10     3.0     5.0     9.0
11  A12    49.0    51.0    50.0
12  A13    27.0    12.0     5.0
13  A14    15.0     6.0     2.0
15  A16    13.0     8.0     4.0
21  A22     5.0     7.0     6.0
22  A23     2.0     3.0    10.0
24  A25     8.0     2.0     1.0
25  A26    10.0    30.0    39.0
31  A32     7.0     9.0    11.0
33  A34    34.0    19.0    12.0
42  A43    16.0    15.0    15.0
43  A44     1.0     1.0     7.0
44  A45     4.0     4.0     3.0
45  A46    32.0    17.0     8.0
46  A47     6.0    10.0    13.0
49  A50    12.0    14.0    17.0
51  A52    29.0    16.0    14.0
   学生序号  sk_num  sm_num  to_num
0    A1    39.0    38.0    34.0
1    A2    50.0    52.0    51.0
2    A3    51.0    44.0    29.0
3    A4    17.0    11.0    18.0
4    A5    45.0    48.0    41.0
5    A6    11.0    18.0    26.0
6    A7    46.0    50.0    52.0
7    A8    36.0    46.0    47.0
8    A9     9.0    13.0    27.0
9   A10     3.0     5.0     9.0
10  A11    52.0    49.0    44.0
11  A12    49.0    51.0    50.0
12  A13    27.0    12.0     5.0
13  A14    15.0     6.0     2.0
14  A15    18.0    21.0    25.0
15  A16    13.0     8.0     4.0
16  A17    23.0    39.0    49.0
17  A18    42.0    43.0    33.0
18  A19    20.0    25.0    23.0
19  A20    14.0    28.0    42.0
20  A21    41.0    42.0    38.0
   学生序号  sk_num  sm_num  to_num
21  A22     5.0     7.0     6.0
22  A23     2.0     3.0    10.0
23  A24    35.0    23.0    20.0
24  A25     8.0     2.0     1.0
25  A26    10.0    30.0    39.0
26  A27    37.0    31.0    31.0
27  A28    25.0    35.0    37.0
28  A29    43.0    37.0    28.0
29  A30    26.0    24.0    19.0
30  A31    38.0    47.0    43.0
31  A32     7.0     9.0    11.0
32  A33    48.0    40.0    32.0
33  A34    34.0    19.0    12.0
34  A35    31.0    33.0    35.0
35  A36    21.0    36.0    46.0
36  A37    30.0    29.0    30.0
37  A38    28.0    22.0    24.0
38  A39    40.0    45.0    48.0
39  A40    44.0    32.0    21.0
   学生序号  sk_num  sm_num  to_num
40  A41    47.0    26.0    16.0
41  A42    19.0    20.0    22.0
42  A43    16.0    15.0    15.0
43  A44     1.0     1.0     7.0
44  A45     4.0     4.0     3.0
45  A46    32.0    17.0     8.0
46  A47     6.0    10.0    13.0
47  A48    24.0    34.0    40.0
48  A49    22.0    27.0    36.0
49  A50    12.0    14.0    17.0
50  A51    33.0    41.0    45.0
51  A52    29.0    16.0    14.0
   学生序号  sk_num  sm_num  to_num
0    A1    39.0    38.0    34.0
1    A2    50.0    52.0    51.0
2    A3    51.0    44.0    29.0
3    A4    17.0    11.0    18.0
4    A5    45.0    48.0    41.0
5    A6    11.0    18.0    26.0
6    A7    46.0    50.0    52.0
7    A8    36.0    46.0    47.0
8    A9     9.0    13.0    27.0
9   A10     3.0     5.0     9.0
10  A11    52.0    49.0    44.0
11  A12    49.0    51.0    50.0
12  A13    27.0    12.0     5.0
13  A14    15.0     6.0     2.0
14  A15    18.0    21.0    25.0
15  A16    13.0     8.0     4.0
16  A17    23.0    39.0    49.0
17  A18    42.0    43.0    33.0
18  A19    20.0    25.0    23.0
19  A20    14.0    28.0    42.0
20  A21    41.0    42.0    38.0
21  A22     5.0     7.0     6.0
22  A23     2.0     3.0    10.0
23  A24    35.0    23.0    20.0
24  A25     8.0     2.0     1.0
25  A26    10.0    30.0    39.0
26  A27    37.0    31.0    31.0
27  A28    25.0    35.0    37.0
28  A29    43.0    37.0    28.0
29  A30    26.0    24.0    19.0
30  A31    38.0    47.0    43.0
31  A32     7.0     9.0    11.0
32  A33    48.0    40.0    32.0
33  A34    34.0    19.0    12.0
34  A35    31.0    33.0    35.0
35  A36    21.0    36.0    46.0
36  A37    30.0    29.0    30.0
37  A38    28.0    22.0    24.0
38  A39    40.0    45.0    48.0
39  A40    44.0    32.0    21.0
40  A41    47.0    26.0    16.0
41  A42    19.0    20.0    22.0
42  A43    16.0    15.0    15.0
43  A44     1.0     1.0     7.0
44  A45     4.0     4.0     3.0
45  A46    32.0    17.0     8.0
46  A47     6.0    10.0    13.0
47  A48    24.0    34.0    40.0
48  A49    22.0    27.0    36.0
49  A50    12.0    14.0    17.0
50  A51    33.0    41.0    45.0
51  A52    29.0    16.0    14.0
学生序号               A45
数学分析                88
高等代数                91
概率论                 86
微分几何                75
抽象代数                65
数值分析                60
factor0        1.25944
factor1      -0.861429
sfactor0      -1.65734
sfactor1      0.360524
total              465
sk_factors     1.15835
sm_factors     1.32795
sk_num               4
sm_num               4
to_num               3
学生序号               A25
数学分析                87
高等代数                87
概率论                 77
微分几何                92
抽象代数                78
数值分析                63
factor0       0.552753
factor1       -1.68658
sfactor0      -1.45513
sfactor1       1.61455
total              484
sk_factors    0.840744
sm_factors     1.49562
sk_num               8
sm_num               2
to_num               1
学生序号               A44
数学分析               100
高等代数                96
概率论                100
微分几何                65
抽象代数                47
数值分析                50
factor0        2.50855
factor1        -0.1942
sfactor0      -2.44312
sfactor1      -1.01883
total              458
sk_factors     1.92071
sm_factors     1.56379
sk_num               1
sm_num               1
to_num               7

聚类分析

将认识对象进行分类是人类认识世界的一种重要方法,

  • 比如有关世界的时间进程的研究,就形成了历史学,有关世界空间地域的研究,则形成了地理学。
  • 又如在生物学中,为了研究生物的演变,需要对生物进行分类,生物学家根据各种生物的特征,将它 们归属于不同的界、门、纲、目、科、属、种之中。

事实上,分门别类地对事物进行研究,要远比在一个混杂多变的集合中更清晰、明了和细致,这是因为同一类事物会具有更多的近似特性。

  • 通常,人们可以凭经验和专业知识来实现分类。
  • 而聚类分析(cluster analysis)作为一种定量方法,将从数据分析的角度,给出一个更准确、细致的分类工具。

例 2. 由于我国各地区经济发展水平不均衡,加之高等院校原有布局使各地区高等教育发展的起点不一致,因而各地区普通高等教育的发展水平存在一定的差异,不同的地区具有不同的特点。对我国各地区普通高等教育的发展状况进行聚类分析,明确各类地区普通高等教育发展状况的差异与特点,有利于管理和决策部门从宏观上把握我国普通高等教育的整体发展现状,分类制定相关政策,更好的指导和规划我国高教事业的整体健康发展。

指标的原始数据取自《中国统计年鉴,1995》和《中国教育统计年鉴,1995》除以各地区相应的人口数得到十项指标值。其中: x1 为每百万人口高等院校数; x2 为每十万人口高等院校毕业生数; x3 为每十万人口高等院校招生数; x4 为每十万人口高等院校在校生数; x5 为每十万人口高等院校教职工数; x6 为每十万人口高等院校专职教师数; x7 为高级职称占专职教师的比例; x8 为平均每所高等院校的在校生数; x9 为国家财政预算内普通高教经费占国内生产总值的比重; x10 为生均教育经费。

北京 5.96     310     461     1557     931     319     44.36     2615     2.20     13631 
上海 3.39     234     308     1035     498     161     35.02     3052     .90     12665 
天津 2.35     157     229     713     295     109     38.40     3031     .86     9385 
西藏 1.69     26     45     137     75     33     12.10     810     1.00     14199 
河南 .55     32     46     130     44     17     28.41     2341     .30     5714 
广西 .60     28     43     129     39     17     31.93     2146     .24     5139 
宁夏 1.39     48    62     208    77     34    22.70     1500     .42     5377 
贵州 .64     23     32     93     37     16     28.12     1469    .34    5415 
青海 1.48     38     46     151     63     30     17.87     1024     .38     7368 
湖南 .74     42     61     194     61     24     33.06     2618     .47     6477 
浙江 .86     42     71     204     66     26     29.94     2363     .25     7704 
新疆 1.29     47     73     265     114     46     25.93     2060     .37     5719 
福建 1.04     53     71     218     63     26     29.01     2099     .29     7106

考虑一个点集

\[X=\{x_1,x_2,\cdots,x_n\}, x_i\in\mathbf{R}^m \]

假设可以找到一个标准（不是唯一的），以便每个样本可以与特定的组相关联

\[g_k=G(x_i) , k=0,1,\cdots,t \]

通常，每一个组称为类，找到函数$G$的过程称为聚类。不同的聚类算法使用不同的策略把一些元素放在一起并与其它元素分开，这样会产生不同的聚类结果。

聚类和分类不同，

  • 分类是已经知道有哪些类别，然后将各个指标或者变量进行分类。
  • 聚类则是不知道有哪些类别，根据一定的规则进行聚类。

聚类分析可以分为两种：

  • 对于数据，可以对变量（指标）时行分类（相当于数据中的列分类），称为R型聚类
  • 也可以对观测值（事件，样品）进行分类（相当于数据中的行分类），称为Q型聚类
  • R型聚类和Q型聚类在数学上是对称的，没有什么不同

聚类分析的基本原则是： 希望类（族）内的相似度尽可能高，类（族）间的相似度尽可能低（相异度尽可能高）。

聚类的方法上来看，主要是划分聚类和层次聚类。

  • 划分聚类：给定一个n个对象的集合，划分方法构建数据的k 个分区，其中每个分区表示一个类（族）。大部分划分方法是基于距离的，给定要构建的k个分区数，划分方法首先创建一个初始划分，然后使用一种迭代的重定位技术将各个样本重定位，直到满足条件为止。
  • 层次聚类：层次聚类(Hierarchical clustering)可以分为凝聚和分裂的方法；
    • 凝聚也称自底向上法，开始便将每个对象单独为一个族，然后逐次合并相近的对象，直到所有组被合并为一个族或者达到迭代停止条件为止。这种方法是最常用、最基本的一种，称为系统聚类分析或多层次聚类。
    • 分裂也称自顶向下，开始将所有样本当成一个族，然后迭代分解成更小的值。

还有

  • 基于密度的聚类：其主要思想是只要“邻域“中的密度（对象或数据点的数目）超过某个阀值，就继续增长给定的族。也就是说，对给定族中的每个数据点，在给定半径的邻域中必须包含最少数目的点。这样的主要好处就是过滤噪声，剔除离群点。
  • 基于网格的聚类：它把对象空间量化为有限个单元，形成一个网格结构，所有的聚类操作都在这个网格结构中进行，这样使得处理的时间独立于数据对象的个数，而仅依赖于量化空间中每一维的单元数。

常用聚类算法

类别 包括主要算法
划分方法 K-Means算法（K-平均）、K-MEDOIDS算法（K-中心点）、CLARANS算法（基于选择的算法）
层次方法 BIRCH算法（平衡迭代规约和聚类）、CURE算法（代表点聚类）、CHAMELEON算法（动态模型）
基于密度 DBSCAN算法（基于高密度连接区域）、DENCLUE（密度分布函数）、OPTICS算法（对象排序识别）
基于网格 STING算法（统计信息网络）、CLIOUE算法（聚类高维空间）、WAVE-CLUSTER算法（小波变换）
基于模型 统计学方法、神经网络方法

K-Means： K-均值聚类也称为快速聚类法，在最小化误差函数的基础上将数据划分为预定的类数K。该算法原理简单并便于处理大量数据

K-中心点： K-均值算法对孤立点的敏感性，K-中心点算法不采用簇中对象的平均值作为簇中心，而选用簇中离平均值最近的对象作为簇中心

系统聚类： 系统聚类也称为多层次聚类，分类的单位由高到低呈树形结构，且所处的位置越低，其包含的对象越少，但这些对象间的共同特征越多。该聚类方法只适用在小数据量的时候使用，数据量大的时候速度会非常慢

系统聚类分析

Q型聚类分析（样本聚类）是，第一次的时候计算各个样本（一个样本是一类）之间的距离（这个距离可以是绝对距离，也可以是欧几里得距离等等，常用的是Minkowski距离），将距离最小的两个聚成一类，这个时候就少了一类，然后针对新的N个类重新进行聚类（对于刚才由两个类合并的那个类则可以根据一定的规则进行转化，这个规则包括最短距离法(Nearest Neighbor)，最长距离法(Furthest Neighbor)，重心法(Centroid Clustering)，类平均法(Group Linkage)，离差平方和法(Ward Method)等等，），重新聚类后又少了一类，循环进行，一直到还有一类聚类结束。

R型聚类和Q型聚类类似，R型聚类叫做变量聚类，因为是变量所以一个变量有很多数据，这个时候可以根据各个变量之间的相关性系数（就像Q型聚类的“距离”）确定。

Nearest Point Algorithm

\[d(u,v) = \min(dist(u[i],v[j])), \forall i\in u, j\in v \]

其中$u$,$v$是两个类(cluster)

Farthest Point Algorithm

\[d(u, v) = \max(dist(u[i],v[j])) \]

UPGMA algorithm

\[d(u,v) = \sum_{ij} \frac{d(u[i], v[j])}{(|u|*|v|)} \]

其中$|u|$, $|v|$表示$u$和$v$的基数(cardinalities)

WPGMA

\[d(u,v) = (dist(s,v) + dist(t,v))/2 \]

UPGMC algorithm

\[dist(s,t) = ||c_s-c_t||_2 \]

其中$c_s$，$c_t$表示cluster的形心（矩心）。

WPGMC algorithm 与UPGMC类似

Ward, incremental algorithm

\[d(u,v) = \sqrt{\frac{|v|+|s|}{T}d(v,s)^2 + \frac{|v|+|t|}{T}d(v,t)^2 - \frac{|v|}{T}d(s,t)^2} \]

其中$T=|v|+|s|+|t|$。

参考：

scipy.cluster.hierarchy.linkage

算法对应参数 

Nearest Point: single
Farthest Point: complete
UPGMA: average
WPGMA: weighted
UPGMC: centroid
WPGMC: median
incremental algorithm: ward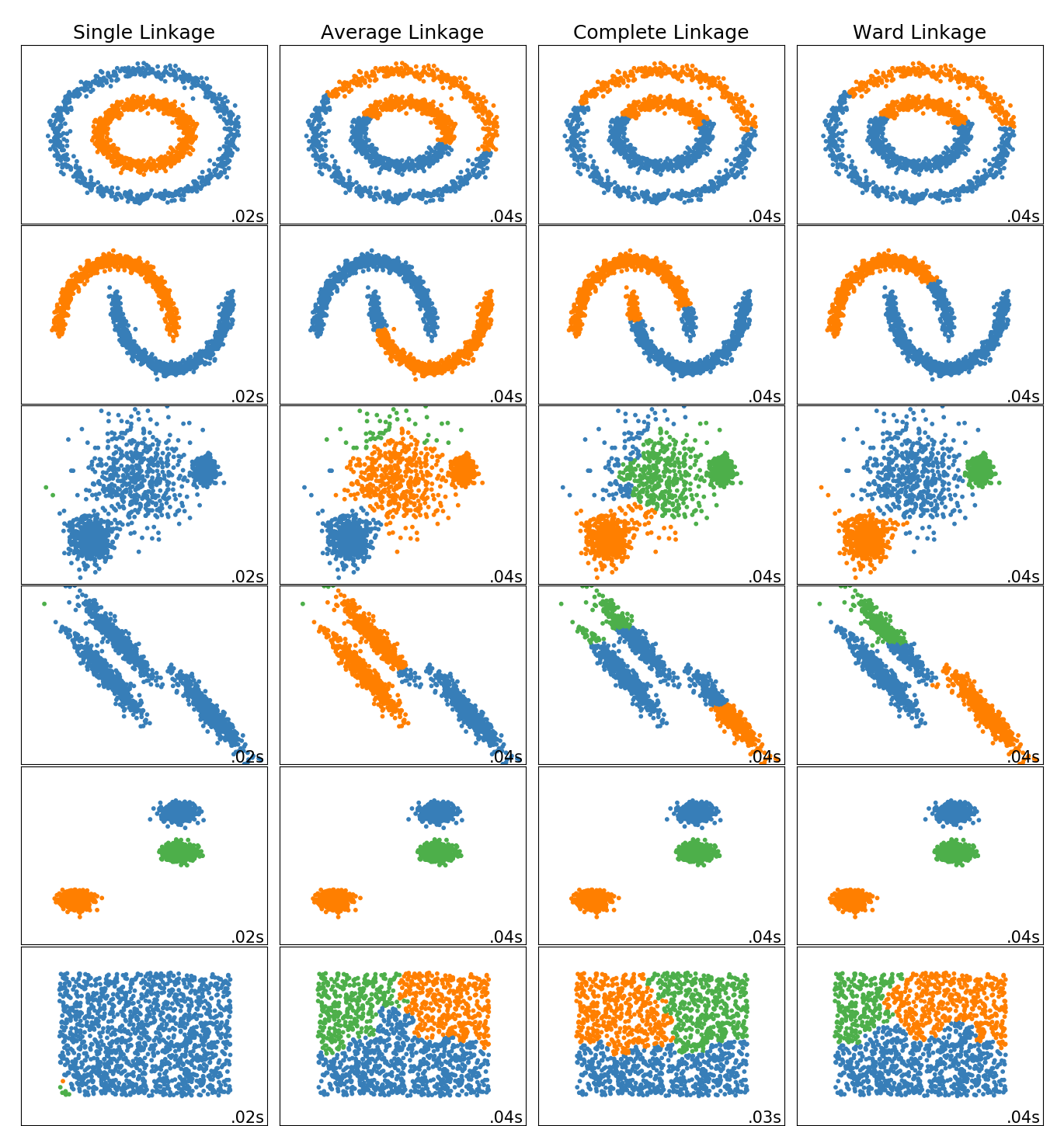

cluster-linkages

例子的分析

  1. 先做R型聚类
    • 在分析或评估过程中,为避免遗漏某些重要因素,往往在一开始选取指标时,尽可能多地考虑所有的相关因素。
    • 而这样做的结果,则是变量过多,变量间的相关度高,给系统分析与建模带来很大的不便。
    • 因此,人们常常希望能研究变量间的相似关系,按照变量的相似关系把它们聚合成若干类,进而找出影响系统的主要因素。

mm7-ex-college-r-tree

可以看到，x2,x3,x4,x5,x6指标之间有较大的相关性。因此，分析时用x1,x2,x7,x8,x9,x10作为分析指标。 

from scipy.cluster import hierarchy  #用于进行层次聚类，话层次聚类图的工具包
from scipy import cluster
from scipy.spatial.distance import pdist
import matplotlib.pyplot as plt

# R型聚类，看变量的相关性
Y = pdist(xdata.T,'correlation')
print(len(Y))
Z = hierarchy.linkage(Y,method='average', metric='correlation')
#Z = hierarchy.linkage(xdata, method ='ward',metric='euclidean')
hierarchy.dendrogram(Z)#,labels = xdata.index) # 画聚类图

plt.show()

UPGMA(参数‘average’)结果

mm7-ex-college-tree

from scipy import stats
# 开始分析
colleges=xdata[['x1','x2','x7','x8','x9','x10']]
colleges=stats.zscore(colleges, axis=0, ddof=1) # 数据标准化
#print(colleges)
Y=pdist(colleges)#, 'mahalanobis')
Z=hierarchy.linkage(Y,method='average')
hierarchy.dendrogram(Z,labels = provinces) # 画聚类图
plt.show()
分为3类
--- 第1类： ['上海', '天津', '陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南', '浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西', '宁夏', '贵州', '青海']
--- 第2类： ['西藏']
--- 第3类： ['北京']
分为4类
--- 第1类： ['上海', '天津']
--- 第2类： ['陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南', '浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西', '宁夏', '贵州', '青海']
--- 第3类： ['西藏']
--- 第4类： ['北京']
分为5类
--- 第1类： ['上海', '天津']
--- 第2类： ['宁夏', '贵州', '青海']
--- 第3类： ['陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南', '浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西']
--- 第4类： ['西藏']
--- 第5类： ['北京']
for i in [3,4,5]:
    print('分为%d类'%i)
    a=[]
    for j in range(i):
        a.append([])
    clu=fcluster(Z, t=i, criterion='maxclust')
    for j in range(len(clu)):
        a[clu[j]-1].append(provinces[j])
    for j in range(i):
        print('---', '第%d类：'%(j+1),a[j])

Python sklearn UPGMA(参数‘average’)结果 

----- average linkage, total 3
第0类： ['上海', '天津', '陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南', '浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西', '宁夏', '贵州', '青海']
第1类： ['北京']
第2类： ['西藏']
----- average linkage, total 4
第0类： ['陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南', '浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西', '宁夏', '贵州', '青海']
第1类： ['上海', '天津']
第2类： ['西藏']
第3类： ['北京']
----- average linkage, total 5
第0类： ['陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南', '浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西']
第1类： ['上海', '天津']
第2类： ['西藏']
第3类： ['北京']
第4类： ['宁夏', '贵州', '青海']
from sklearn.cluster import AgglomerativeClustering
print("===================sklearn Agglomerative Clustering")
for linkage in ('ward', 'average', 'complete'):
  for total in [3,4,5]:
    clustering = AgglomerativeClustering(linkage=linkage, n_clusters=total)
    clustering.fit(colleges)
    print( "----- %s linkage, total %d" % (linkage,total))
    labels=clslabel(clustering.labels_)
    for i in range(total):
        print("第%d类："%i, labels[i])

可以看到，

  • 北京的状况与其他地区相比，有很大的不同。主要表现在每百万人口的学校数量(x1)和每十万人口的学生数量(x2)以及国家财政预算内普通高教经费占国内生产总值的比重(x9)等方面远远高于其他地区。这与北京是全国的政治、经济和文化中心的地位吻合。
  • 上海、天津作为另外两个较早的直辖市,高等教育状况和北京是类似的状况。
  • 西藏作为一个非常特殊的民族地区,被单独聚为一类,主要表现在每百万人口高等院校数(x1)比较高,国家财政预算内普通高教经费占国内生产总值的比重(x9)和生均教育经费也相对较高(x10),而高级职称占专职教师的比例(x7)与平均每所高等院校的在校生数(x8)又都是全国最低的。
  • 宁夏、贵州和青海的高等教育状况极为类似,高等教育资源相对匮乏。

K-Means聚类

算法基于k个初始的均值这样的强初始条件来确定类的数量

\[K^{(0)}=\{\mu^{(0)}_1,\cdots,\mu_k^{(0)}\} \]

然后，计算每个样本和每个均值的距离，并将样本分配给距离最小的类，这种方法通常被称为类的惯性最小化,

\[SS_{W_i}=\sum_t ||x_t-\mu_i||^2, \forall i \in (1,k) \]

这是一个迭代过程，一旦所有的样本都被处理后，就会计算出一组新的均值$K^{(1)}$，并重新计算所有的距离，直到均值稳定从而使得惯性最小，算法停止。

  1. 方法对初始条件非常敏感
  2. 算法具有强假设条件，需要聚类具有凸性
  3. DBSCAN算法可以解决非凸问题

Python sklearn K-Means算法得到的结果(样本数少，不适合用) 

====================sklearn kmeans
--total 3--
第0类： ['西藏', '宁夏', '青海']
第1类： ['北京', '上海', '天津']
第2类： ['陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南', '浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西', '贵州']
--total 4--
第0类： ['天津', '陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南']
第1类： ['北京', '上海']
第2类： ['浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西', '宁夏', '贵州', '青海']
第3类： ['西藏']
--total 5--
第0类： ['浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西', '宁夏', '贵州']
第1类： ['北京']
第2类： ['西藏', '青海']
第3类： ['陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南']
第4类： ['上海', '天津']
print("====================sklearn kmeans")
from sklearn.cluster import KMeans
for total in [3,4,5]:
    kmeans = KMeans(n_clusters=total, random_state=0).fit(colleges)
    print("--total %d--"%total)
    labels=clslabel(kmeans.labels_)
    for i in range(total):
        print("第%d类："%i, labels[i])

目录