曲线拟合

最小二乘法

张瑞
中国科学技术大学数学科学学院

曲线拟合

  • 插值是一种构造一个近似函数逼近原函数的手段。
  • 在实际应用中，观察到的数据会包含误差。
  • 插值这种手段会把误差也包含在近似函数中，特别是可能数据中某个点的误差特别大。

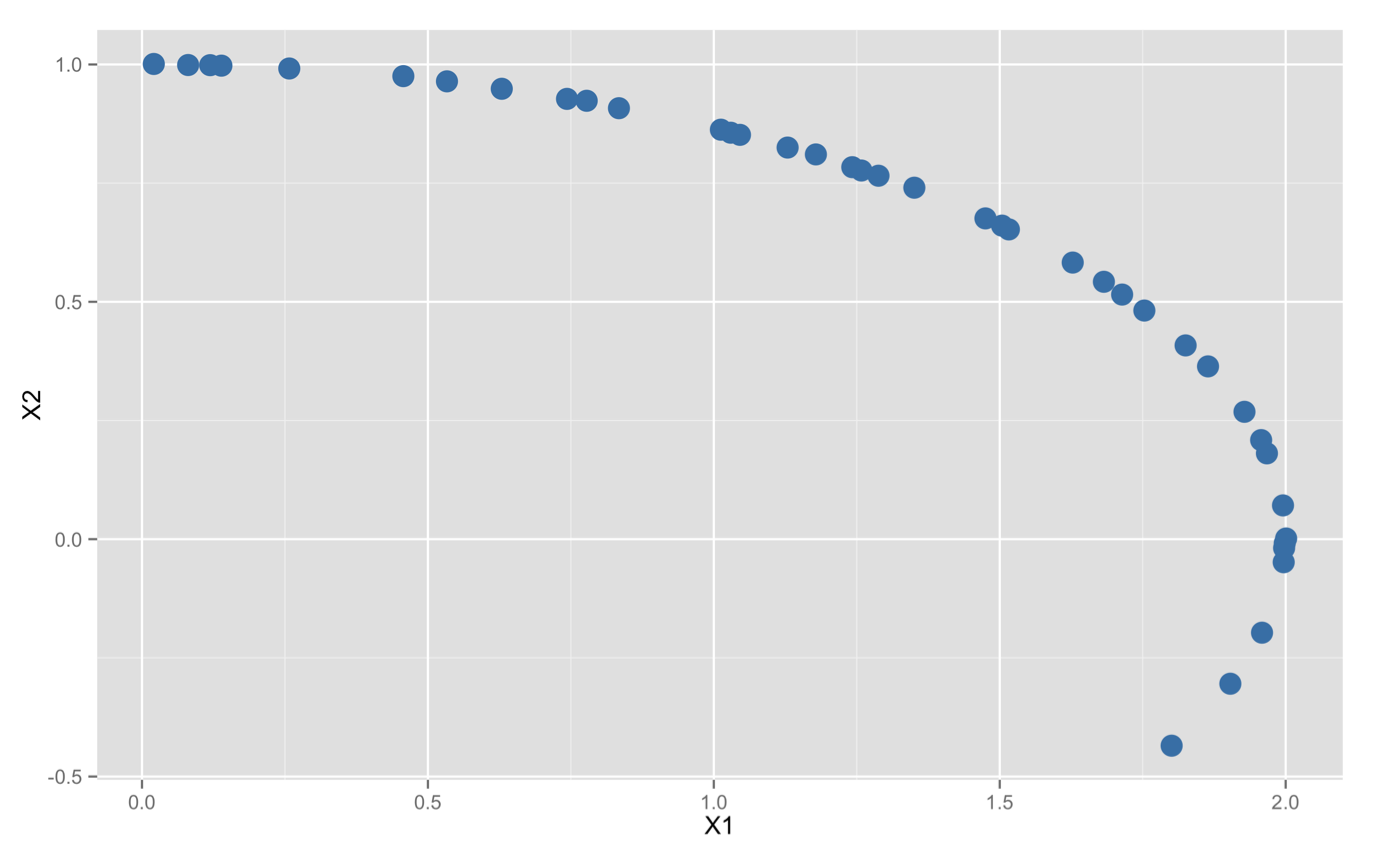
例 1. 已知行星的运行轨道是一个椭圆。几百个观测数据，这些数据会带有误差，因此它们几乎不可能满足同一个椭圆方程。如何计算行星的运行轨道？

lsq-planet-orbit

例 2. 一个风景区有若干个风景点，要修条直线的公路，使得这条公路“靠近”所有的风景点？

注. 这两个问题，有共同的数学特性：

  • 从一组已知的点，如何构造一个近似函数，使得这个函数足够“靠近”这些点？
  • 这个函数可以不通过所有的点。

拟合的定义

定义 1.
$f(x)$是定义在区间$[a,b]$上的函数，$x_i$, $i=0,\cdots,n$是$[a,b]$区间上互不相同的点。$\Phi$是已知的函数空间。 在$\Phi$上找函数$g(x)$，使得$g(x)-f(x)$在某种范数意义下最小。函数$g(x)$称为$f(x)$的拟合函数。

注. 拟合同插值类似，都是构造近似函数的手段。

注. 范数可以用来度量线性空间中两个向量之间的距离，当然也可以度量函数空间中两个函数是否靠近。

最小二乘问题

定义 2.
在拟合问题中，取$f(x)-g(x)$的范数为2-范数的话，得到的问题就叫作最小二乘问题(Least Square)。 即，找$g(x)$，使得

\[\|f(x)-g(x)\|_2=\sqrt{\sum_{i=0}^n(f(x_i)-g(x_i))^2} \]

达到最小。

注. 若找$g(x)$满足$\displaystyle\sum_{i=0}^n|f(x_i)-g(x_i)|$最小，就称为最小一乘问题。

$g(x)$在空间$\Phi$中，则令

\[g(x)=a_0\phi_0(x)+a_1\phi_1(x)+\cdots+a_m\phi_m(x) \]

其中$\Phi=span\{\phi_0(x),\phi_1(x),\cdots,\phi_m(x)\}$。

问题变为：找$a_0, a_1,\cdots, a_m$使得

\[G=\sum_{i=0}^n(f(x_i)-[a_0\phi_0(x_i)+a_1\phi_1(x_i)+\cdots+a_m\phi_m(x_i)])^2 \]

达到最小。$G=G(a_0,a_1,\cdots,a_m)$是一个多元函数。

多元函数的最小值点必须满足

\[\frac{\partial G}{\partial a_j}=0, \forall j=0,1,\cdots,m \]

由$G$的表达式，

\[\frac{\partial G}{\partial a_j}=\sum_{i=0}^n\left(-2\left(f(x_i)-[a_0\phi_0(x_i)+a_1\phi_1(x_i)+\cdots+a_m\phi_m(x_i)]\right)\phi_j(x_i)\right) \]
\[\frac{\partial^2 G}{\partial a_j\partial a_k}=\sum_{i=0}^n2\phi_j(x_i)\phi_k(x_i) \]

这样，$G$达到最小时，系数要满足

\[\sum_{i=0}^n[a_0\phi_0(x_i)+a_1\phi_1(x_i)+\cdots+a_m\phi_m(x_i)]\phi_j(x_i)=\sum_{i=0}^nf(x_i)\phi_j(x_i) \]

即有

\[\begin{aligned} a_0\sum_{i=0}^n\phi_0(x_i)\phi_j(x_i)+a_1\sum_{i=0}^n\phi_1(x_i)\phi_j(x_i)+\cdots \\ +a_m\sum_{i=0}^n\phi_m(x_i)\phi_j(x_i)=\sum_{i=0}^nf(x_i)\phi_j(x_i) \end{aligned} \]

定义

\[(\phi,\psi)=\sum_{i=0}^n\phi(x_i)\psi(x_i) \]

则可以简写上式为

\[\begin{aligned} a_0(\phi_0,\phi_j)+a_1(\phi_1,\phi_j)+\cdots+a_m(\phi_m,\phi_j)=(f,\phi_j) \\ j=0,1,\cdots,m \end{aligned} \]

这样，可以得到如下的线性方程组

\[\begin{pmatrix} (\phi_0,\phi_0) & (\phi_1,\phi_0) & \cdots & (\phi_m,\phi_0) \\ (\phi_0,\phi_1) & (\phi_1,\phi_1) & \cdots & (\phi_m,\phi_1) \\ \vdots & \vdots & \cdots & \vdots \\ (\phi_0,\phi_m) & (\phi_1,\phi_m) & \cdots & (\phi_m,\phi_m) \\ \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_m \end{pmatrix} =\begin{pmatrix} (f,\phi_0) \\ (f,\phi_1) \\ \vdots \\ (f,\phi_m) \end{pmatrix} \]

称为法方程。

例 3. 有数据

x -4 -2 1 2 4
y 14.2 2.3 1.4 2.0 4.3

试对数据分别做如下的拟合：

(1).$y=a+bx$ , (2).$y=ax^2+b$, (3).$y=a x^2+b x+c$,

(4).$y=ae^{bx}$, (5).$y=a x^b$, (6).$y=\frac{1}{a+bx}$

解. (1) 可以确定基函数为$1$, $x$，则可以列出法方程

\[\begin{pmatrix} (1,1) & (1,x) \\ (x,1) & (x,x) \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} =\begin{pmatrix} (f,1) \\ (f,x) \end{pmatrix} \]
\[\begin{pmatrix} \sum 1 & \sum x_i \\ \sum x_i & \sum x_i^2 \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} =\begin{pmatrix} \sum y_i \\ \sum y_i x_i \end{pmatrix} \]
========= a+bx ===========
Coefficients:  [ 5.05392157 -1.06960784]
Matrix:  [[  5.   1.]
 [  1.  41.]]
RHS: [ 24.2 -38.8]

(2) 基函数为$x^2$, $1$，则有

\[\begin{pmatrix} \sum x_i^4 & \sum x_i^2 \\ \sum x_i^2 & \sum 1 \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} =\begin{pmatrix} \sum y_i x_i^2 \\ \sum y_i \end{pmatrix} \]
========= ax^2+b ===========
Coefficients:  [ 0.55632184  0.27816092]
Matrix:  [[ 545.   41.]
 [  41.    5.]]
RHS: [ 314.6   24.2]

(3) 基函数为$x^2$, $x$, $1$，则有

\[\begin{pmatrix} \sum x_i^4 & \sum x_i^3 & \sum x_i^2 \\ \sum x_i^3 & \sum x_i^2 & \sum x_i \\ \sum x_i^2 & \sum x_i & \sum 1 \end{pmatrix} \begin{pmatrix} a \\ b \\ c \end{pmatrix} =\begin{pmatrix} \sum y_i x_i^2 \\ \sum y_i x_i \\ \sum y_i \end{pmatrix} \]
========= ax^2+bx+c ===========
Coefficients:  [ 0.52261905 -0.97738095  0.75      ]
Matrix:  [[ 545.    1.   41.]
 [   1.   41.    1.]
 [  41.    1.    5.]]
RHS: [ 314.6  -38.8   24.2]

(4) 依据最小二乘问题的定义，问题变为找$a$, $b$使得

\[\sum_{i}(y_i-a e^{bx_i})^2 \]

达到最小。这看起来比较困难。

将函数两边取对数，有

\[\ln y=\ln a+ b x \]
  • 先对数据$(x_i, \ln y_i)$做基函数为$1$, $x$的拟合，得到$\tilde y=\tilde a+\tilde b x$，
  • 然后，取
    \[y=e^{\tilde y}=e^{\tilde a}e^{\tilde b x} \]

注. 这样得到的系数并不能满足最小二乘的定义，但它确实满足某种范数意义下的最小。

法方程为

\[\begin{pmatrix} \sum 1 & \sum x_i \\ \sum x_i & \sum x_i^2 \end{pmatrix} \begin{pmatrix} \tilde a \\ \tilde b \end{pmatrix} =\begin{pmatrix} \sum \tilde y_i \\ \sum \tilde y_i x_i \end{pmatrix} \]

其中$\tilde y_i=\ln y_i$。 

========= a e^{bx} ===========
Coefficients:  [ 1.22387925 -0.1450107 ]
Matrix:  [[  5.   1.]
 [  1.  41.]]
RHS: [ 5.97438553 -4.72155942]

注. 代码由python3编写，调用 numpy.linalg.solve 来解 法方程

fitting-ex8

矛盾方程组

问题. 行星的运行轨道是一个椭圆。现在有成百上千的观测数据，如何确定这个行星的运行轨道？

解. 这些观测数据应该满足同一个椭圆方程

\[ax^2+bxy+cy^2+dx+ey=1 \]

即有

\[ax_i^2+bx_iy_i+cy_i^2+dx_i+ey_i=1 , i=1,2,3,\cdots \]

这是一个5个未知量，很多个方程的线性方程组。方程的个数比未知量的个数要多，这是一个矛盾方程组。

  • 1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。
  • 经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。
  • 随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。
  • 时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星
  • 高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》。

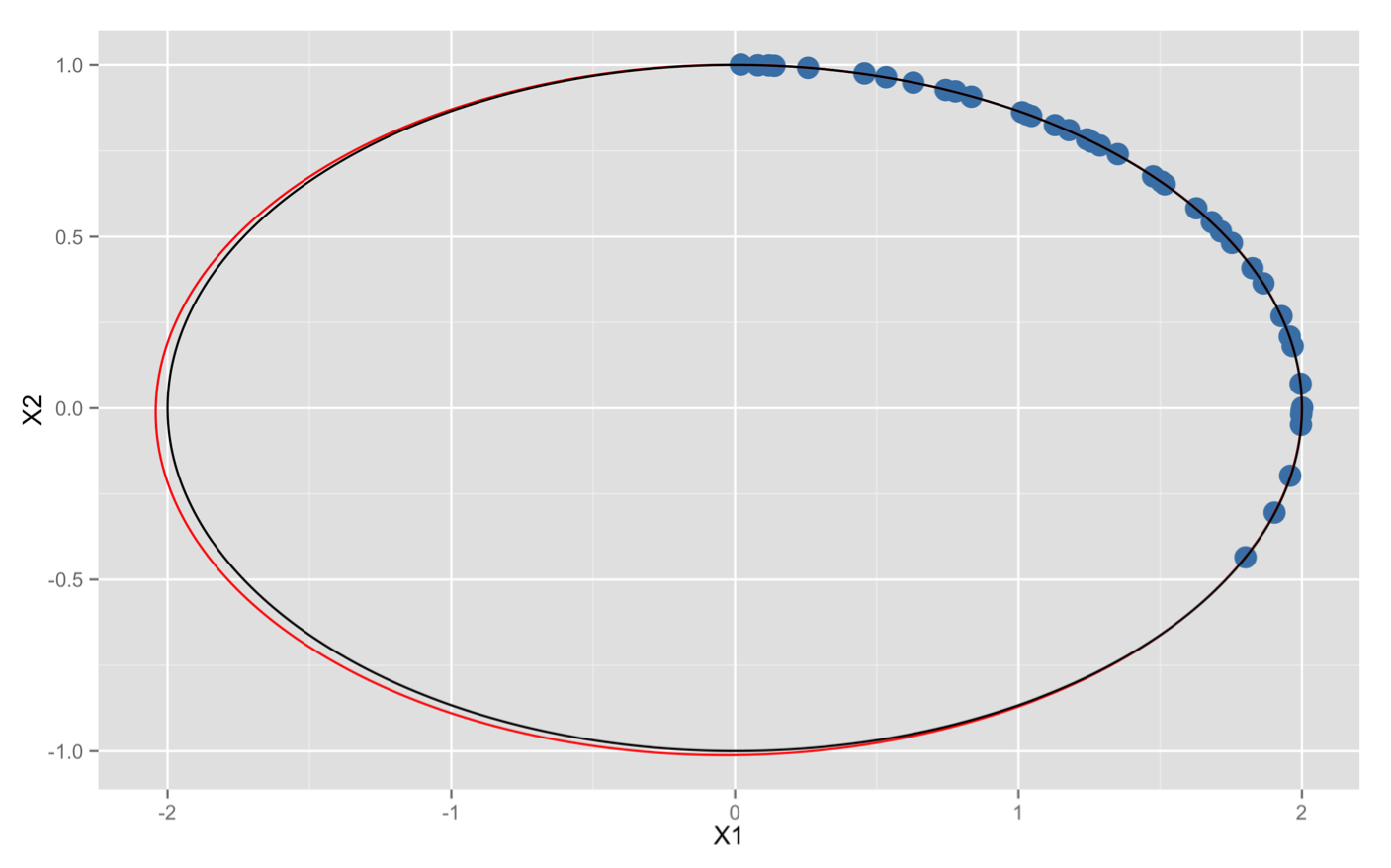
lsq-planet-orbit-result

黑线是真正的小行星轨道，红线是线性最小二乘法估计出来的轨道。

定理 1.
设线性方程组$Ax=b$的系数矩阵$A=(a_{ij})_{m\times n}$，则

  1. $rank(A^TA)=rank(A^T)=rank(A)$
  2. 线性方程组$A^TAx=A^Tb$恒有解。

若进步有$rank(A)=n$，则

  1. 矩阵$A^TA$是对称正定矩阵；
  2. $n$阶线性方程组$A^TAx=A^Tb$有唯一的解。

定理 2.
$x$满足$\displaystyle\min_{y\in \mathbb{R}^n}\|Ay-b\|_2^2$的充要条件是$x$满足$A^TAx=A^Tb$。

证明. 若$Ax=0$，则有$A^TAx=0$，

同时，若$A^TAx=0$，则$x^TA^TAx=0$，即$\|Ax\|_2^2=0$，从而$Ax=0$。

也就是说，$Ax=0$当且仅当$A^TAx=0$，它们同解，从而$rank(A^TA)=rank(A^T)$

又有，

\[rank(A^TA)\leq rank(A^TA,A^Tb)=rank(A^T(A,b))\leq rank(A^T) \]

则有$rank(A^TA)=rank(A^TA,A^Tb)$，即方程$A^TAx=A^Tb$恒有解。

证明. 由$rank(A)=n$，则存在可逆阵$P$，使得$PA=\begin{pmatrix} \bar A \\ \bar 0_1 \end{pmatrix}$，其中$A$是一个$n\times n$的可逆阵， $\bar 0_1$是$(n-m)\times n$的零矩阵。则

\[(PA)(PA)^T=PAA^TP^T=\begin{pmatrix} \bar A \\ \bar 0_1 \end{pmatrix} \begin{pmatrix} \bar A^T & \bar 0_1^T \end{pmatrix} =\begin{pmatrix} \bar A \bar A^T & \bar 0_1^T \\ \bar 0_1 & 0 \end{pmatrix} \]

则有$rank(AA^T)=rank(PAA^TP^T)=rank(\bar A\bar A^T)=n$，即有 $rank(A^TA)=rank(AA^T)=n$

证明. （定理2）： 令$y=x+(y-x)=x+e$，其中$x$满足$A^TAx=A^Tb$，则

\[\begin{aligned} \|Ay-b\|_2^2=&(Ax-b+Ae)^T(Ax-b+Ae)\\ =&(Ax-b)^T(Ax-b)+(Ae)^T(Ax-b) \\ & +(Ax-b)^T(Ae)+(Ae)^T(Ae) \\ =&\|Ax-b\|_2^2+\|Ae\|_2^2 \\ & +e^TA^T(Ax-b)+(Ax-b)^TAe\\ \end{aligned} \]

注意到

\[\begin{aligned} ((Ax-b)^TAe)^T=&e^TA^T(Ax-b) \\ =&e^T(A^TAx-A^Tb)=0 \end{aligned} \]

则有

\[\|Ay-b\|_2^2=\|Ax-b\|_2^2+\|Ae\|_2^2 \]

即，当且仅当$y=x$时，$\|Ax-b\|_2^2$达到最小。

如前例中，对于5个数据点，用解矛盾方程组的方法来拟合$y=ax^2+b$。 如前数据，得到矛盾方程组

\[\begin{cases} a x_0^2+b=y_0 \\ a x_1^2+b=y_1 \\ a x_2^2+b=y_2 \\ a x_3^2+b=y_3 \\ a x_4^2+b=y_4 \\ \end{cases} \, \Rightarrow \, \begin{pmatrix} x_0^2 & 1 \\ x_1^2 & 1 \\ x_2^2 & 1 \\ x_3^2 & 1 \\ x_4^2 & 1 \\ \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} =\begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix} \]

求解最小二乘问题

\[\begin{pmatrix} x_0^2 & x_1^2 & x_2^2 & x_3^2 & x_4^2 \\ 1 & 1 & 1 & 1 & 1 \end{pmatrix}\left[ \begin{pmatrix} x_0^2 & 1 \\ x_1^2 & 1 \\ x_2^2 & 1 \\ x_3^2 & 1 \\ x_4^2 & 1 \\ \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} =\begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix}\right] \]

可以得到

\[\begin{pmatrix} \sum x_i^4 & \sum x_i^2 \\ \sum x_i^2 & \sum 1 \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} =\begin{pmatrix} \sum x_i^2 y_i \\ \sum y_i \end{pmatrix} \]

与前面得到的法方程是一样的

在拟合问题中，用$m$次多项式来拟合$n+1$个数据点时：

  1. $m<n$时，可以得到矛盾方程组的矩阵为
    \[A=\begin{pmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^m \\ 1 & x_1 & x_1^2 & \cdots & x_1^m \\ 1 & x_2 & x_2^2 & \cdots & x_2^m \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1 & x_n & x_n^2 & \cdots & x_n^m \\ \end{pmatrix} \]
    根据Vandermonde行列式的特性知，$rank(A)=m$。此时，矛盾方程组的解存在唯一。
  1. $m=n$时，可以得到唯一的一条插值多项式$L_n(x)$。由
    \[\|f(x)-L_n(x)\|_2^2=\sum_{i=0}^n(f(x_i)-L_n(x_i))^2=0 \]
    知，$L_n(x)$是$f(x)$的拟合函数。
  2. $m>n$时，通过$n+1$个点的$m$次多项式有无穷多条，这无穷条插值多项式都是拟合函数。此时，拟合函数存在不唯一。

法方程的病态性

当做多项式拟合的时候，以$1, x, x^2, \cdots, x^m$得到的法方程很可能是病态的。如何降低法方程的病态性？

问题. 如果法方程是一个对角阵，则一定没有病态性的问题。 能否找到$\phi_i$，使得$(\phi_i,\phi_j)=0, \forall i\neq j$？

注意到$(\phi,\psi)$满足如下特性：

  • $(\phi,\psi)=(\psi,\phi)$
  • $(\phi_1+\phi_2,\psi)=(\phi_1,\psi)+(\phi_2,\psi)$
  • $(a\phi,\psi)=a(\phi,\psi)$, $\forall a\in\mathbb{R}$
  • $(\phi,\phi)\geq 0$；而且$(\phi,\phi)=0$当且仅当$\phi(x_i)=0$

具有内积的特性。

问题. 对于多项式函数的基函数$1,x,x^2,\cdots,x^m$，是否可以变为另一组基函数 $\phi_0(x),\phi_1(x),\cdots,\phi_m(x)$， 使得

\[(\phi_i(x),\phi_j(x))=0, \forall i\neq j \]

Schmidt正交化过程：

  1. $\phi_0(x)=1$
  2. $\displaystyle\phi_1(x)=x-\frac{(x,\phi_0(x))}{(\phi_0(x),\phi_0(x))}\phi_0(x)$
  3. $\displaystyle\phi_j(x)=x^j-\sum_{k=1}^{j-1}\frac{(x^j,\phi_k(x))}{(\phi_k(x),\phi_k(x))}\phi_k(x)$, $j=1,2,\cdots,n$

注. 当节点$x_i$变化后，$(\phi(x),\psi(x))$的定义也不同了，因此$\phi_i(x)$也会不同。

例 4. 有节点组

\[x_i=10+\frac{i}{5}, i=0,1,2,3,4,5 \]

对如下两组基函数，分别计算法方程矩阵的条件数

(1) $1, x, x^2$

(2) $1$, $x-10.5$, $(x-10.3)(x-10.7)$

解. 作为作业完成

取$f(x)=1+\ln(x)$，对于基函数$1, x, x^2$， Python中使用Decimal类型，采用6位小数计算，得到对应的系数为 

Coefficients:  [Decimal('7.82965') Decimal('-0.948494') Decimal('0.0496562')]

采用16位小数计算，得到系数是 

Coefficients:  [Decimal('1.850147483432168') Decimal('0.190651845528236')
 Decimal('-0.004540738661120082')]

fitting-illness

连续函数的逼近

除了在一组离散点上要求$g(x)$拟合$f(x)$外，同样可以在一个区间上要求$g(x)$逼近$f(x)$。

例 5. (例2.2) 构造$\phi(x)=ax+b$，在$[-1,1]$上逼近$f(x)=e^x$。

解. 首先定义范数为

\[\|\phi(x)-f(x)\|_2=\sqrt{\int_{-1}^1 (\phi(x)-f(x))^2dx} \]

这样，得到一个最小二乘问题。找$\phi(x)$使得

\[Q=\int_{-1}^1 (\phi(x)-f(x))^2dx \]

达到最小。

定义

\[(f(x),g(x))=\int_{-1}^1 f(x)g(x)dx \]

它满足内积的要求，

\[\begin{aligned} (f(x), g(x))=&(g(x), f(x)) \\ (\alpha f(x)+\beta g(x), h(x))=&\alpha(f(x), h(x))+\beta(g(x), h(x)) \end{aligned} \]

这样，

\[\begin{aligned} Q=&\int_{-1}^1 (\phi(x)-f(x))^2dx \\ =&(\phi(x)-f(x), \phi(x)-f(x)) \\ =&(\phi, \phi)-2(\phi, f)+(f,f) \end{aligned} \]

又

\[(\phi, \phi)=(ax+b, ax+b) =a^2(x,x)+2ab(x,1)+b^2(1,1) \]
\[-2(\phi, f)=-2(ax+b, f(x)) =-2[a(x,f(x))+b(1, f(x))] \]

因此$Q$取到最小值时，$a$,$b$应该满足

\[\begin{aligned} \frac{\partial Q}{\partial a}=2a(x,x)+2b(x,1)-2(x,f(x))=0 \\ \frac{\partial Q}{\partial b}=2a(x,1)+2b(1,1)-2(1,f(x))=0 \\ \end{aligned} \]

即

\[\begin{pmatrix} (x,x) & (x,1) \\ (1,x) & (1,1) \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} =\begin{pmatrix} (x,f(x)) \\ (1, f(x)) \end{pmatrix} \]

得到，$Q$最小时$a$,$b$应该满足

\[\begin{pmatrix} (x,x) & (x,1) \\ (1,x) & (1,1) \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} =\begin{pmatrix} (x,f(x)) \\ (1, f(x)) \end{pmatrix} \]

其中

\[\begin{aligned} (x,x)=&\int_{-1}^1 x^2dx=\frac23 , & (x,1)=\int_{-1}^1 x dx=0 ,\\ (1,1)=&\int_{-1}^1 1dx=2 & \\ (x,f(x))=&\int_{-1}^1 xe^xdx=2e^{-1}, & \\ (1, f(x))=&\int_{-1}^1 e^xdx=e-e^{-1} \end{aligned} \]

最终的法方程为，

\[\begin{pmatrix} \frac23 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} =\begin{pmatrix} 2e^{-1} \\ e-e^{-1} \end{pmatrix} \]

谢谢

事实上，在连续函数的逼近中，取区间为$[-\pi, \pi]$，函数为

\[\phi(x)=a_0+\sum_{n=1}^{\infty}(a_n\sin(nx)+b_n\cos(nx)) \]

就是Fourier分析

目录

本节读完

例 6. 为什么不是最小一乘法或者最小三乘法比较好？

6.

  • 最小二乘估计的意义在于且仅在于：如果数据的观测误差是高斯分布的，那么最小二乘解就是使得观测数据的出现概率最大的解。
  • 而一旦观测误差不是高斯分布的，最小二乘估计就失去了它独特的地位。例如，早在高斯发明最小二乘法之前几十年，最小一乘法就已经出现了，它对应的是观测误差服从拉普拉斯分布。

可是广义误差分布允许无数种可能的尺度，为什么只有最小二乘法才被最广泛的应用呢？

  1. 一来，这要归功于拉普拉斯证明了中心极限定理，即：任何随机误差（不包括系统误差），如果是由多种独立的微小误差相加组合而成的，那么它的分布一定趋近于高斯分布。现实生活中大部分的观测误差来源都较为复杂，可以看成多种微小误差的叠加。例如我们可以想象皮亚奇的误差来自于空气不好+镜片不好+眼歪+手抖+那美克星超新星爆发…等等，它的总体概率分布趋近于高斯分布，因此最小二乘法会取得最好的效果。
  2. 二来，其实也有很多数据是不符合高斯分布的，例如机器学习中常常提到的长尾(long tail)的数据,经常服从拉普拉斯分布，对他们来说最小一乘才是更好的解法。但是最小一乘法的目标函数中有一个绝对值，这对优化算法来说非常不友好。所以虽然最小一乘法比最小二乘法发明的更早，但是直到二十世纪最优化算法得到了长足的发展之后，最小一乘法才逐渐受到重用。