微分
复习
|
张瑞
中国科学技术大学数学科学学院
rui [at] ustc [dot] edu [dot] cn |
复习
微分
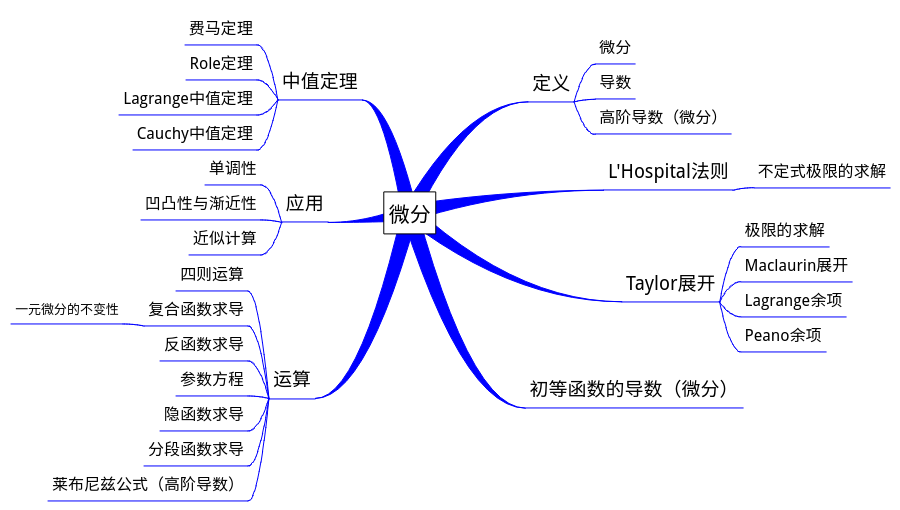
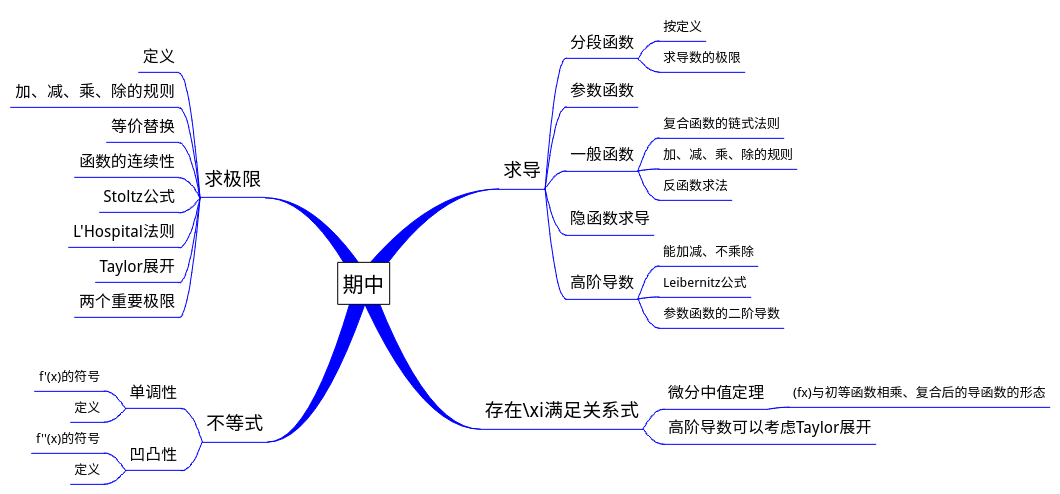
习题
例 1. 求
例 2. 求
例 3. 求
例 4. 函数在附近有三阶连续导数,, , 。设满足, ,求
例 5. 已知,则在处是否连续?是否可导?
例 6. 设 。求
例 7. 设是的反函数,求
例 8. 设,其中在点的邻域内有阶连续导数,求
例 9. ,,证明存在,并求它
例 10. 函数在上具有二阶导数,且,。证明:
- 在内至少存在一个实根
- 在内至少存在两个不同的实根
例 11. 在上二阶可导,,且有
证明