一元函数的积分学

复习题

张瑞
中国科学技术大学数学科学学院

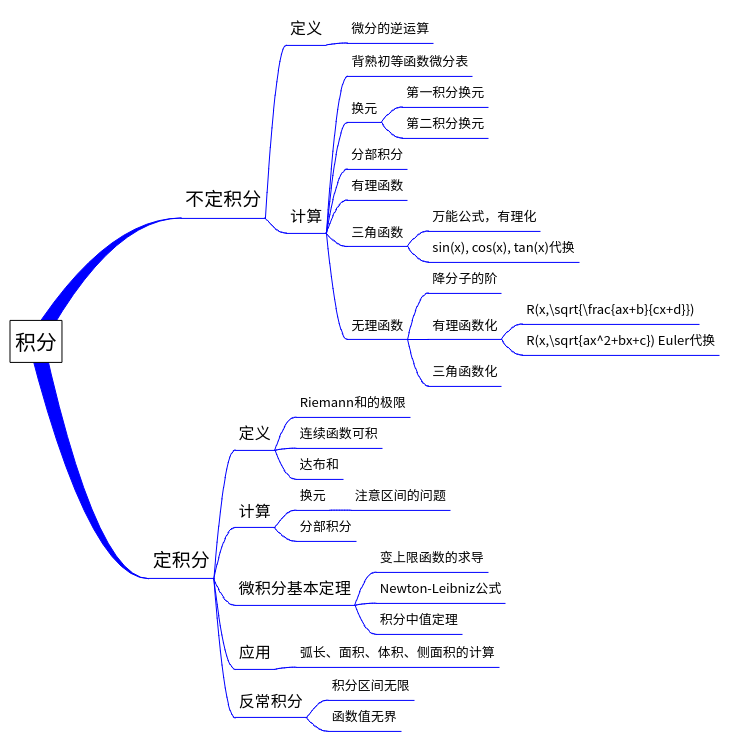
chap4

习题

换元

例 1. 求积分

\[\int\dfrac{1}{\sqrt{x}(1+x)}dx \]

例 2. 求积分

\[\int\dfrac{e^{\arctan x}+x\ln(1+x^2)}{1+x^2}dx \]

vertical slide 2

三角函数代换

例 3. 求积分

\[\int\dfrac{1}{(x^2-a^2)^{\frac32}}dx , a>0 \]

例 4. 求积分

\[\int\dfrac{1}{x^4\sqrt{1+x^2}}dx \]

直接去根号

例 5. 求积分

\[\int\dfrac{1}{1+\sqrt{x-1}}dx \]

例 6. 求积分

\[\int\dfrac{1}{\sqrt{1+e^{2x}}}dx \]

谢谢

分部积分

例 7. 求积分

\[\int e^{3x}(\cot^2x-3\cot x+1)dx \]

例 8. 求

\[\int\frac{\ln(x+\sqrt{1+x^2})}{(1+x^2)^{\frac32}}dx \]

谢谢

定积分的变量代换

需要注意：

  1. 变量代换函数的连续性
  2. 变量代换函数的值域
  3. 原函数在积分区间内没有瑕点

例 9. 求积分

\[\int_0^{2n\pi}\dfrac{1}{\sin^4x+\cos^4x}dx , n\in Z \]

谢谢

对称性的应用

例 10. 求积分

\[\int_{-1}^1\dfrac{x^2(1+\sin x)}{1+\sqrt{1-x^2}}dx \]

例 11. 求积分

\[\int_{-\frac{\pi}2}^{\frac{\pi}2}\dfrac{\cos^4x}{1+e^{-x}}dx \]

谢谢

例 12. 计算

\[I=\int_{\frac12}^2(1+x-\frac1x)e^{x+\frac1x}dx \]

例 13.  

chap4-wifi

例 14. 由$\int_0^af(x)dx=\int_0^af(a-x)dx$，求

\[\int_{0}^{\pi}\dfrac{x\sin x}{1+\cos^2{x}}dx=I, \int_0^{\frac{\pi}2}\dfrac{\sin^2x}{\sin x+\cos x}dx=J \]

例 15. $f(x)$在$[0,b]$上可积，则有

\[\int_0^b\dfrac{f(x)}{f(x)+f(b-x)}dx=\dfrac{b}2 \]

并求

\[\int_{0}^{\frac{\pi}2}\dfrac{\cos x}{\cos x+\sin x}dx=J \]

谢谢

证明

例 16. 设$f''(x)$在$[0,\pi]$上连续，$f(\pi)=2$，且

\[\int_0^{\pi}(f(x)+f''(x))\sin xdx=5 \]

求$f(0)$

例 17. 已知

\[\int_0^y e^{t^2}dt+\int_0^{\sin x}\cos^2tdt=0 \]

求$\dfrac{dy}{dx}$

谢谢

例 18. $f(x)$连续，

\[F(t)=\int_1^t(\int_y^tf(x)dx)dy \]

求$F'(2)$

例 19. 求积分$\displaystyle\int_0^1x\int_1^x\frac{\sin t^2}tdtdx$

例 20. 求 $\displaystyle\lim_{x\to\infty}\dfrac{(\int_0^x e^{t^2}dt)^2}{\int_0^{x^2}e^tdt}$

谢谢

例 21. $f(x)$在$[a,b]$上可积，且有

\[|f(x_1)-f(x_2)|\leq|x_1-x_2|,\forall x_1,x_2\in[a,b] \]

证明

\[\int_a^bf(x)dx\leq(b-a)f(a)+\dfrac12(b-a)^2 \]

例 22. $f(x)$在$[a,b]$上连续，且单调递减。 证明

\[\int_a^b xf(x)dx\leq\dfrac{a+b}2 \int_a^b f(x)dx \]

谢谢

例 23. $f(x)$在$[a,b]$上连续，且恒大于$0$。 证明，存在唯一$c\in[a,b]$，满足

\[\int_a^c f(t)dt=\int_c^b \dfrac1{f(t)}dt \]

例 24. $f(x)$在$[a,b]$上可导，且严格单调增。$g(y)$是$f(x)$的原函数。 证明，

\[\int_a^b f(x)dx=bf(b)-af(a)-\int_{f(a)}^{f(b)}g(y)dy \]

谢谢

例 25. 函数$f(x)$在$[0,1]$上具有二阶导数，且$f(0)=0$, $f(1)=1$, $\displaystyle\int_0^1f(x)dx=1$。证明：

(1) 存在$\xi\in(0,1)$，满足$f'(\xi)=0$

(2) 存在$\eta\in(0,1)$，满足$f''(\eta)<-2$

目录

例 26.  

\[\lim_{x\to\infty}\dfrac{(\int_0^x e^{t^2}dt)^2}{\int_0^{x^2}e^tdt} \]

谢谢