曲线拟合
最小二乘法
|
张瑞
中国科学技术大学数学科学学院
rui@ustc.edu.cn |
曲线拟合
- 插值是一种构造一个近似函数逼近原函数的手段。
- 在实际应用中,观察到的数据会包含误差。
- 插值这种手段会把误差也包含在近似函数中,特别是可能数据中某个点的误差特别大。
例 1. 已知行星的运行轨道是一个椭圆。几百个观测数据,这些数据会带有误差,因此它们几乎不可能满足同一个椭圆方程。如何计算行星的运行轨道?
例 2. 一个风景区有若干个风景点,要修条直线的公路,使得这条公路“靠近”所有的风景点?
注. 这两个问题,有共同的数学特性:
- 从一组已知的点,如何构造一个近似函数,使得这个函数足够“靠近”这些点?
- 这个函数可以不通过所有的点。
拟合的定义
定义 1.
是定义在区间上的函数,, 是区间上互不相同的点。是已知的函数空间。
在上找函数,使得在某种范数意义下最小。函数称为的拟合函数。
注. 拟合同插值类似,都是构造近似函数的手段。
注. 范数可以用来度量线性空间中两个向量之间的距离,当然也可以度量函数空间中两个函数是否靠近。
最小二乘问题
定义 2.
在拟合问题中,取的范数为2-范数的话,得到的问题就叫作最小二乘问题(Least Square)。
即,找,使得
达到最小。
注. 若找满足最小,就称为最小一乘问题。
在空间中,则令
其中。
问题变为:找使得
达到最小。是一个多元函数。
多元函数的最小值点必须满足
由的表达式,
这样,达到最小时,系数要满足
即有
定义
则可以简写上式为
这样,可以得到如下的线性方程组
称为法方程。
例 3. 有数据
| x | -4 | -2 | 1 | 2 | 4 |
| y | 14.2 | 2.3 | 1.4 | 2.0 | 4.3 |
试对数据分别做如下的拟合:
(1). , (2)., (3).,
(4)., (5)., (6).
解. (1) 可以确定基函数为, ,则可以列出法方程
========= a+bx ===========
Coefficients: [ 5.05392157 -1.06960784]
Matrix: [[ 5. 1.]
[ 1. 41.]]
RHS: [ 24.2 -38.8](2) 基函数为, ,则有
========= ax^2+b ===========
Coefficients: [ 0.55632184 0.27816092]
Matrix: [[ 545. 41.]
[ 41. 5.]]
RHS: [ 314.6 24.2]
(3) 基函数为, , ,则有
========= ax^2+bx+c ===========
Coefficients: [ 0.52261905 -0.97738095 0.75 ]
Matrix: [[ 545. 1. 41.]
[ 1. 41. 1.]
[ 41. 1. 5.]]
RHS: [ 314.6 -38.8 24.2](4) 依据最小二乘问题的定义,问题变为找, 使得
达到最小。这看起来比较困难。
将函数两边取对数,有
- 先对数据做基函数为, 的拟合,得到,
- 然后,取
注. 这样得到的系数并不能满足最小二乘的定义,但它确实满足某种范数意义下的最小。
法方程为
其中。
========= a e^{bx} ===========
Coefficients: [ 1.22387925 -0.1450107 ]
Matrix: [[ 5. 1.]
[ 1. 41.]]
RHS: [ 5.97438553 -4.72155942]注.
代码由python3编写,调用 numpy.linalg.solve 来解 法方程
矛盾方程组
问题. 行星的运行轨道是一个椭圆。现在有成百上千的观测数据,如何确定这个行星的运行轨道?
解. 这些观测数据应该满足同一个椭圆方程
即有
这是一个5个未知量,很多个方程的线性方程组。方程的个数比未知量的个数要多,这是一个矛盾方程组。
- 1801年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。
- 经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。
- 随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。
- 时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星
- 高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》。
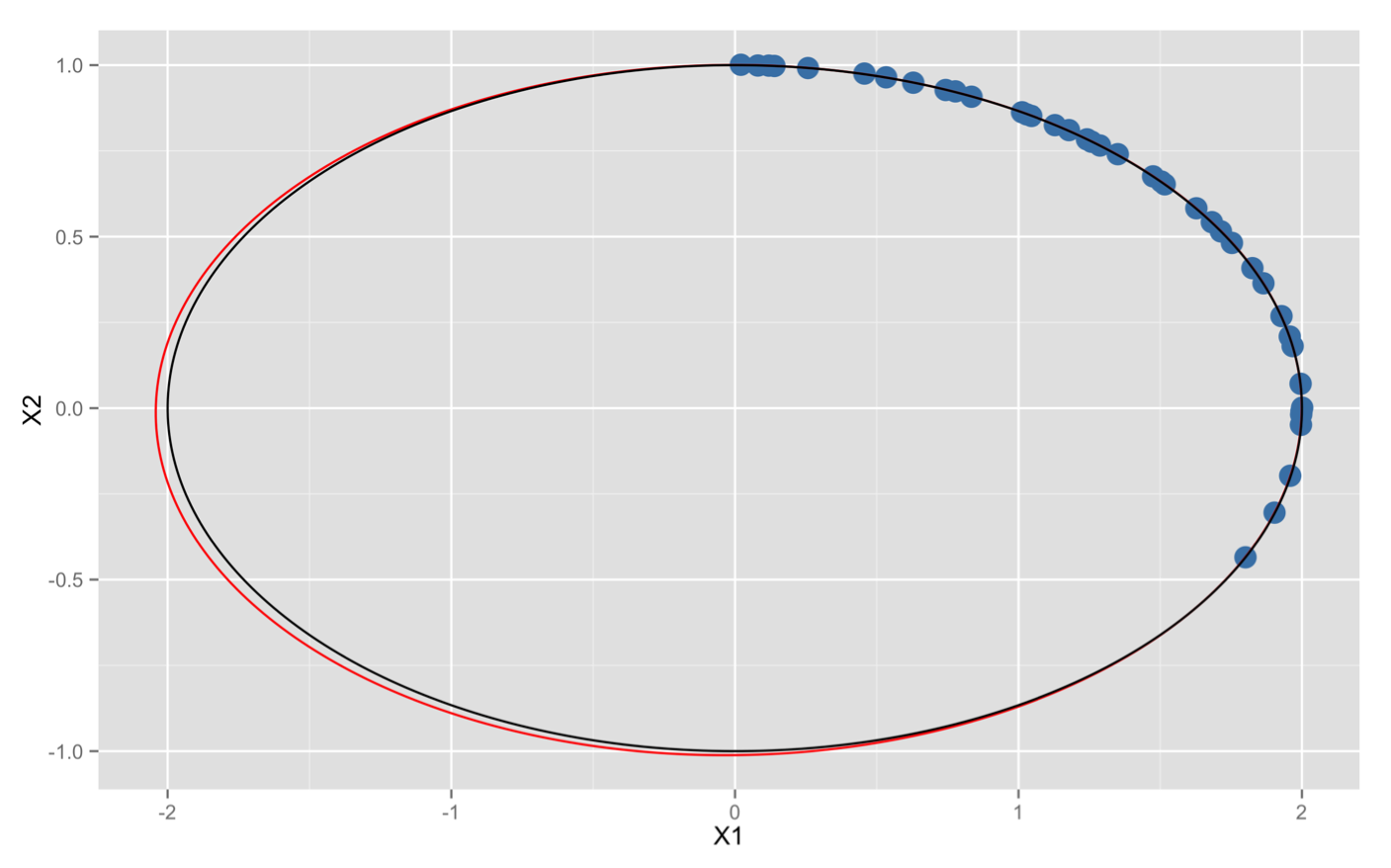
黑线是真正的小行星轨道,红线是线性最小二乘法估计出来的轨道。
定理 1.
设线性方程组的系数矩阵,则
- 线性方程组恒有解。
若进步有,则
- 矩阵是对称正定矩阵;
- 阶线性方程组有唯一的解。
定理 2.
满足的充要条件是满足。
证明. 若,则有,
同时,若,则,即,从而。
也就是说,当且仅当,它们同解,从而
又有,
则有,即方程恒有解。
证明. 由,则存在可逆阵,使得,其中是一个的可逆阵, 是的零矩阵。则
则有,即有
证明. (定理2): 令,其中满足,则
注意到
则有
即,当且仅当时,达到最小。
如前例中,对于5个数据点,用解矛盾方程组的方法来拟合。 如前数据,得到矛盾方程组
求解最小二乘问题
可以得到
与前面得到的法方程是一样的
在拟合问题中,用次多项式来拟合个数据点时:
- 时,可以得到矛盾方程组的矩阵为
根据Vandermonde行列式的特性知,。此时,矛盾方程组的解存在唯一。
- 时,可以得到唯一的一条插值多项式。由
知,是的拟合函数。
- 时,通过个点的次多项式有无穷多条,这无穷条插值多项式都是拟合函数。此时,拟合函数存在不唯一。
法方程的病态性
当做多项式拟合的时候,以得到的法方程很可能是病态的。如何降低法方程的病态性?
问题. 如果法方程是一个对角阵,则一定没有病态性的问题。 能否找到,使得?
注意到满足如下特性:
- ,
- ;而且当且仅当
具有内积的特性。
问题. 对于多项式函数的基函数,是否可以变为另一组基函数 , 使得
Schmidt正交化过程:
- ,
注. 当节点变化后,的定义也不同了,因此也会不同。
例 4. 有节点组
对如下两组基函数,分别计算法方程矩阵的条件数
(1)
(2) , ,
解. 作为作业完成
取,对于基函数, Python中使用Decimal类型,采用6位小数计算,得到对应的系数为
Coefficients: [Decimal('7.82965') Decimal('-0.948494') Decimal('0.0496562')]采用16位小数计算,得到系数是
Coefficients: [Decimal('1.850147483432168') Decimal('0.190651845528236')
Decimal('-0.004540738661120082')]连续函数的逼近
除了在一组离散点上要求拟合外,同样可以在一个区间上要求逼近。
例 5. (例2.2) 构造,在上逼近。
解. 首先定义范数为
这样,得到一个最小二乘问题。找使得
达到最小。
定义
它满足内积的要求,
这样,
又
因此取到最小值时,,应该满足
即
得到,最小时,应该满足
其中
最终的法方程为,
谢谢
事实上,在连续函数的逼近中,取区间为,函数为
就是Fourier分析
本节读完
例 6. 为什么不是最小一乘法或者最小三乘法比较好?
6.
- 最小二乘估计的意义在于且仅在于:如果数据的观测误差是高斯分布的,那么最小二乘解就是使得观测数据的出现概率最大的解。
- 而一旦观测误差不是高斯分布的,最小二乘估计就失去了它独特的地位。例如,早在高斯发明最小二乘法之前几十年,最小一乘法就已经出现了,它对应的是观测误差服从拉普拉斯分布。
可是广义误差分布允许无数种可能的尺度,为什么只有最小二乘法才被最广泛的应用呢?
- 一来,这要归功于拉普拉斯证明了中心极限定理,即:任何随机误差(不包括系统误差),如果是由多种独立的微小误差相加组合而成的,那么它的分布一定趋近于高斯分布。现实生活中大部分的观测误差来源都较为复杂,可以看成多种微小误差的叠加。例如我们可以想象皮亚奇的误差来自于空气不好+镜片不好+眼歪+手抖+那美克星超新星爆发…等等,它的总体概率分布趋近于高斯分布,因此最小二乘法会取得最好的效果。
- 二来,其实也有很多数据是不符合高斯分布的,例如机器学习中常常提到的长尾(long tail)的数据,经常服从拉普拉斯分布,对他们来说最小一乘才是更好的解法。但是最小一乘法的目标函数中有一个绝对值,这对优化算法来说非常不友好。所以虽然最小一乘法比最小二乘法发明的更早,但是直到二十世纪最优化算法得到了长足的发展之后,最小一乘法才逐渐受到重用。