P. 90(4)

(a) 阶的第一类贝塞耳函数的定义如下：

证明（形式地）这个级数给出了贝塞耳方程：

的解。

注：为the Euler Gamma function。

注：这里的p不一定是自然数，它可以是任意实数。

注：验证即可，有推导兴趣的同学可以参考“数学物理方程(科大版p.84)”。

(b) 如果是整数，试证：

注：  (这是由Gamma函数的性质得到的！)，例如：

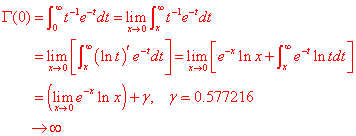
(c) 证明:

它可充当带有整数下标的贝塞耳函数的母函数。

注：交换求和顺序及其符号的有效性

注： (这是由Gamma函数的性质得到的！同上注释。)

(d) 证明:

注：可能需要用到一个记号

(e) 证明:

注：注意积分的上下限，写出详细推导过程。

Input by zjzheng