P.95 Laplace方法 (最速下降法、鞍点法)：

问题表述：

求积分

在很大时的渐近展开式

方法思想：

对积分进行变换，直至对大值，积分结果的主要贡献来源于积分路径上的一小部分为止。

假设该积分部分在附近，那么就采用在该点附近对被积函数作Taylor展开进行化简。

解题思路：

记

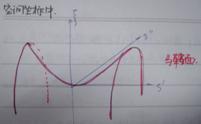
若找到一个对被积函数贡献最大的路径，为xoy平面内红色线的路径

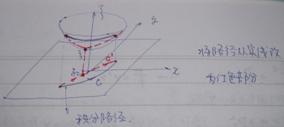
过点使有极小值，通过点的路径，下降最快

和为共轭调和函数，故其等值线正交，证明如下：

-------------------------

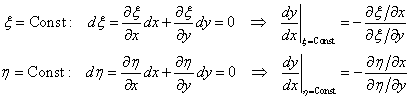
则：

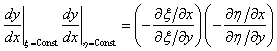
因为是和为共轭调和函数，我们有

因此：

所以等值线正交。

-------------------------

因此沿着的线，有最速下降

在点：，故

又因为沿着C’线，

所以沿着C’线，

引进复变数使得

则：

实部：

虚部：

沿s平面的实轴：和

沿s平面的虚轴：和

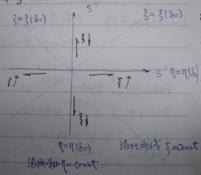
s平面，的等值线如图，都是马鞍面，原点为鞍点

由有，

所以

如果很大，则当时迅速下降

将在s = 0点展开：

, , , …

所以：

因为, 所以

则

又因为

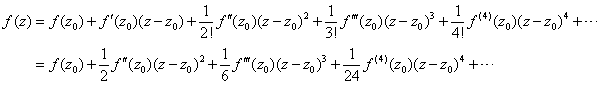
其中 （因为是的极值点）

即有

-------------------------------------------------

零阶近似：

--------------------------------------------------

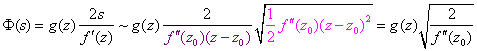
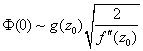
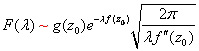
下面求更高阶的近似

假定：

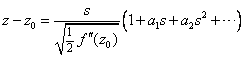
那么：

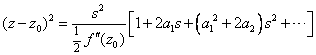
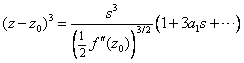
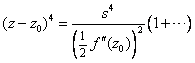
代入得：

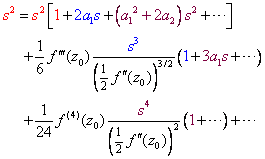
比较上式两边关于s的幂级数的系数，我们有：

即有：

因此：

则：

把代入并进一步整理得：

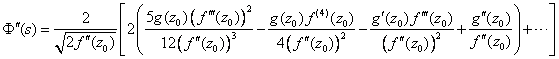
二阶近似：

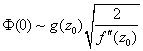
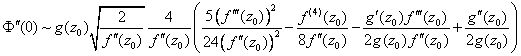
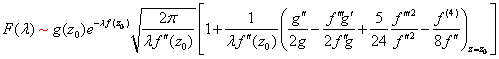
类似上述过程可以等到更高阶的近似，因为基本方法已经示明，所以这里不再赘述。

参考资料：

《Linear and Nonlinear waves》G.B. Whitham