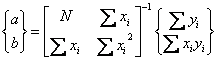1. 符号书写及其含义：

a)

b)

c) 恒等于、等于、约等于、近似于、~ 渐近于、正比于、趋近于、远小于、远大于

---------------------------------------------------------------------------------------------------------------------------

α.Α.alpha   β.Β.beta      γ.Γ.gamma     δ.Δ.delta        ε.Ε.epsilon   ζ.Ζ.zeta       η.Η.eta           θ.Θ.theta
ι.Ι.iota        κ.Κ.kappa   λ.Λ.lambda    μ.Μ.mu          ν.Ν.nu          ξ.Ξ.xi          ο.Ο.omicron   π.Π.pi
ρ.Ρ.rho      σ.Σ.sigma    τ.Τ.tau           υ.Υ.upsilon     φ.Φ.phi         χ.Χ.chi        ψ.Ψ.psi          ω.Ω.omega

---------------------------------------------------------------------------------------------------------------------------

2. 函数及其性质：

a) 常用函数

i. 指数函数和对数函数

 (1748年，复数的欧拉公式)                

ii. 三角函数及其反函数

iii. 双曲函数及其反函数

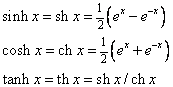
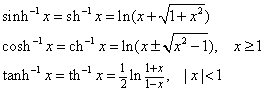
iv. Euler函数

v. 超几何函数：

vi. 其他一些函数

正弦积分：

余弦积分：

指数积分：

对数积分：

Fresnel积分：

误差函数：

补余误差函数：

正态概率积分：

b) 函数的性质

i. 函数的极限：L’Hospital法则

若，则

若，则

ii. 函数的极值：

极大值；极小值

iii. 的条件极值：

构造辅助函数

求解，其中为Lagrange因子

c) 函数之间的关系 (补充题)

i.

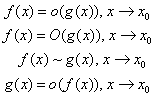
d) 函数的展开

i. 二项式展开：

ii. Taylor展开：

, (Maclaurin)

(Taylor)

,

3. 积分：

a) 定积分：Riemann和的极限：

b) 分部积分：

c) Dirichlet积分：

d) Fresnel积分：

4. 积分变换及其反演：

若，则称为Fourier核。

a) Laplace变换及其反演：

b) 梅林变换：

c) 阶亨克而变换：

d) Fourier余弦变换：

e) Fourier正弦变换：

f) Fourier变换：

g) 有限Fourier余弦变换：

h) 有限Fourier正弦变换：

5. 方程：

a) 代数方程：

b) 微分方程：

i. 可分离变量方程：

ii. 齐次方程：

iii. 线性方程：

iv. 不显含未知量的方程：

v. 不显含自变量的方程：

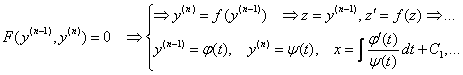
c) 差分方程：P.103 (习题P112.8)

i. 差分方程：

ii. 左边=

iii. 右边第一项=

iv. 右边第二项=

v. 右边=

vi.

vii.

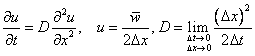
6. 数值方法：

a) Newton- Raphson迭代：

i. 非线性方程组：

ii. 迭代格式：

b) 最小二乘法：(习题P182.6)

i. 矛盾方程组：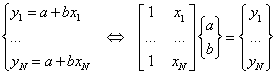

ii.

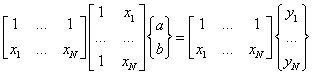
iii.   i.e.