1. 函数的极限

设函数在区域内有定义。

如果对，总能找到，使得当时，均有，

则称当趋于时，的极限值为，记作

。

2. 函数的连续性

如果

，

则称函数在点连续。

如果函数在区域D的每点都连续，则称在区域D中连续。

3. 导数

4. 解析

如果函数在区域D内的每一点可微，则称在D内解析，称是D内的解析函数；

如果函数在点的某个邻域内可微，则称点解析；

如果函数在点不解析，则称为的奇点。

5. 积分

Riemann和的极限：

6. 函数关系

远小于：

如果，

则称当趋于时，函数远小于函数，记作

渐近量级(阶符号)：

如果对附近的是有界的，即，

则称当趋于时，函数最多时函数的量级，记作

渐近函数：

如果 或 ，即，

则称当趋于时，函数渐近于函数，记作

远大于：

如果，

则称当趋于时，函数远大于函数，记作

7. 常微分方程

n阶常微分方程：

线性微分方程：

线性微分算子：

8. 齐次线性方程

n阶齐次线性方程：

通解：

是任意积分常数，是各自满足Eq.(1.4)的线性无关的函数组。

9. 非齐次线性方程

10. 非线性微分方程

11. 本征值问题

12. 差分方程

13. 展开式

二项式展开：

Taylor级数展开式：

Maclaurin级数展开式：

渐近级数：

渐近展开式： 可以证明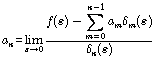：，渐近级数是渐近展开式的一种特例。

14. 常用幂级数展开式

, (Maclaurin)

(Taylor)

,

15. 积分变换及其反演：

若，则称为Fourier核。

Laplace变换及其反演：

梅林变换：

阶亨克而变换：

Fourier余弦变换：

Fourier正弦变换：

Fourier变换：

有限Fourier余弦变换：

有限Fourier正弦变换：

16.

<<< 基本物理概念

1.

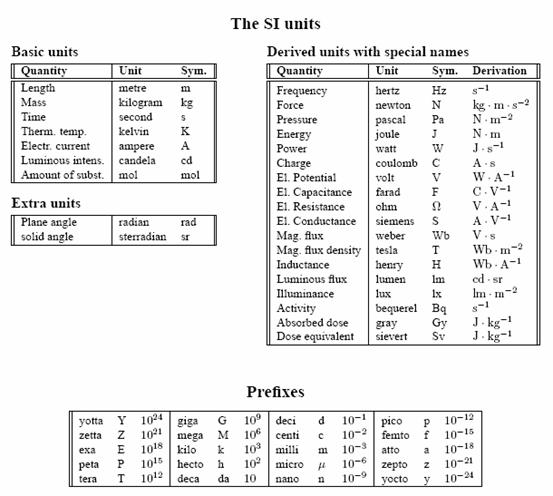
2.

3.

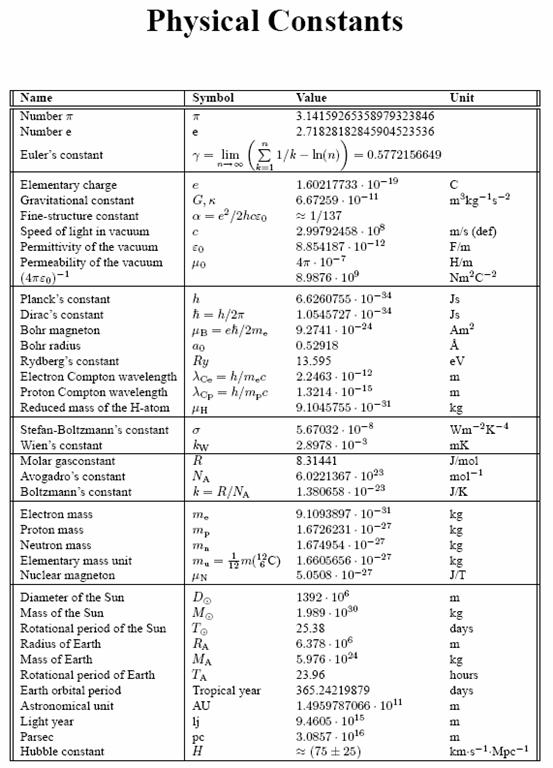
4.