Mathematics Applied to Deterministic Problem in the Natural Sciences
Part A: An overview of the interaction of mathematics and natural science
Chapter 1: What's applied mathematics
§1.1On the nature of applied mathematics
Formulation → Solution → Interpretation
§1.2 Introduction to the analysis of galactic structure
1. Physical laws governing galactic behavior
(1) Newton's law's of motion and his law of universal gravitation, which govern all classical mechanics
(2) The laws of electrodynamics according to the formulation of Maxwell
(3) The laws of thermodynamics
2. Dynamics of stellar systems
3. Application Distribution of stars across a galactic disk
Characteristics
§1.3 Aggregation of slime mold amoebae
1. Some facts about slime mold amoebae
2. Formulation of a mathematical model

3. Analysis of aggregation onset as an instability
Chapter 2: Deterministic systems and ordinary differential equations
§2.1 Planetary obits
1. Kepler's laws and the law of universal gravitation
2. The inverse problem: Orbits of planets and comets

3. Planetary orbits according to the general theory of relativity
![]()
4. N particles: A deterministic system
5. Linearity
§2.2 Elements of perturbation theory, including Poincare's method for periodic orbits
1. Perturbation theory, elementary consideration
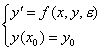
eg. 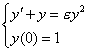
2. The simple pendulum and the successive approximation to its motion

* (1) o; (2) O;

3. Perturbation series applied to the pendulum problem
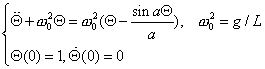
4. Poincare's perturbation theory
§2.3 A system of ordinary differential equations
1. The initial value problems statement of theorems
2. Example of nonuniqueness
* (1) Function space; (2) Bifurcation strenge attractor; (3) Lorenz's equation;
Chapter 3: Random processes and partial differential equations
§3.1 Random walk in one dimension; Langevin's equation
1. The 1-D random walk model
2. Mean, variance and generating function
3. Langevin’s equation
§3.2 Asymptotic series, Laplace's method, gamma function, Stirling's formula
1. An example: Asymptotic expansion via parts integration
2. Definition in the theory of asymptotic expansions
3. Laplace’s method
4. Development of the asymptotic Stirling series for the Gamma function
§3.3 A difference equation and its limit
1. A difference equation for probability function of the random walk
2. Approximation of the difference equation by a differential equation
3. Solutions of the differential equation for the probability
4. Reflecting and absorbing barriers
§3.4 Further considerations pertinent to the relationship between probability and partial differential equations
1. Super position of fundamental solutions: the method of images
2. Laplace’s equation related to random walk
Chapter 4: Superposition, heat flow and Fourier analysis
§4.1 Conduction of heat
1. Differential equation for 1-D, 3-D heat condition
2. Solution by the method of separation of variables
§4.2 Fourier theorem
1. Sum of Fourier sine series
2. Full-range and half-range Fourier series
§4.3 Integration and differentiation of Fourier series
1. Fourier series
2. Gibbs phenomenon
3. Approximation with least squared error
4. Bessel’s inequality, Parseval’s theorem and Reiz-Fisher theorem
Chapter 5: Further developments in Fourier Analysis
§5.1 Other aspects of heat conduction
1. Variation of temperature underground
2. Numerical integration of the heat equation
3. Heat conduction in a nonuniform medium
§5.2 Sturm-Liouville systems
1. Properties of eigenvalue and eigenfunction
2. Orthogonality and normalization
3. Expansion in terms of eigenfunctions
4. Asymptotic approximation to eigenvalues and eigenfunctions
§5.3 Brief introduction to Fourier transform
1. Fourier transform formulas and the Fourier identity
2.Solution of the equation by Fourier transform
§5.4 Generalized harmonic analysis
1. Introduction
2. Fourier analysis of a truncated sinusoided function
3. Generalization to stationary time sequences
4. Autocorrelation function and the power spectrum
Part B: Some Fundamental Procedures Illustrated on Ordinary Differential Equations
Chapter 6: Simplification dimensional analysis and scaling
§6.1 The basic simplification procedure
1. Illustrations of the procedure
eg1. ![]() eg2.
eg2. 
2. Two chastening examples
eg3. ![]()
3. Conditioning and sensitivity
4. Zeros of function
5. Second order differential equations
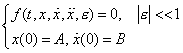 eg1.
eg1. 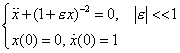 eg2.
eg2. 
§6.2 Dimensional analysis
1. Patting a differential equation into dimensionless form
2. Π theorem
§6.3 Scaling
1. Definition of scaling

2. Scaling known functions
![]()
eg1. ![]()
eg2. ![]()
eg3. ![]()
3. Orthodoxy (regularity)
4. Scaling unknown functions
Chapter 7: Regular perturbation theory
§7.1 The series method applied to the simple pendulum

Chapter 8:
§8.1 Physical formulation and dimensional analysis of a model for “standing gradient” osmotically driven flow
§8.2 A mathematical model and its dimensional analysis
1. Conservation of fluid mass
2. Conservation of solute mass
3. Boundary conditions
4. Introduction of dimensionless variables
5. Possibility of a scale model for standing gradient flow
§8.3 Obtaining the final scaled dimensionless equation of the mathematical model
1. Scaling
2. Estimating the size of the dimensionless parameters
3. An unsuccessful regular perturbation calculation
4. Relation between parameters
5. Final formulation
§8.4 Solution and interpretation
Chapter 9: Introduction of singular perturbation theory
§9.1 Roots of polynomial equations
eg1. ![]() eg2.
eg2. ![]()
§9.2 Boundary value problems for ordinary differential equations
![]()
1. A study on the exact solution of a model equation
2. Find an approximate solution by singular perturbation method
3. Matching
4. Basic procedures
![]() eg1.
eg1.  eg2.
eg2. 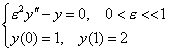
Chapter 10: Singular perturbation theory applied to a problem in biochemical kinetics
§10.1 Formulation of an initial value problem for a one enzyme-one substrate chemical reaction
1. The law of mass action
2. Enzyme catalysis
3. Scaling and final formulation
§10.2 Approximate solution by singular perturbation method
1. Inner solution
2. Outer solution
3. Matching
4. Higher approximation
Chapter 11: Three techniques applied to the simple pendulum
§11.1 Stability of normal and inverted equilibrium of the pendulum
1. Determining stability of equilibrium
![]()
§11.2 A multiple scale expansion
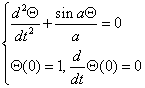 eg1.
eg1.  eg2.
eg2. ![]()
§11.3 The phase plane
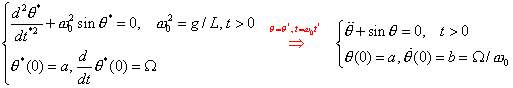
![]()
1. The phase portrait of an undamped simple pendulum
2. Separatrixes
3. Critical points
4. Limit cycles
5. Behavior of trajectories near critical points
eg. ![]()
,S·A·
未及时交的作业本请送到力一楼
)
9
,