P.61 庞加莱方法

控制方程：

庞加莱表示：(我们考虑最一般的情况)

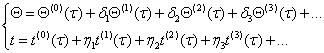
其中：(各小量之间的关系)

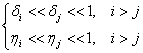
因为：

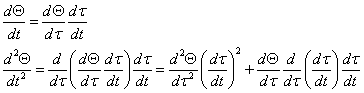
考虑到控制方程变化后我们希望含的项不出现，因此其系数为零，我们有：

为了方便，当时，我们希望，因此取，其意义是自变量的平移对问题的解决不会起关键性的作用。所以自变量的庞加莱表示可以写成：

取，(自变量的放大倍数，可以任意取值)，则：

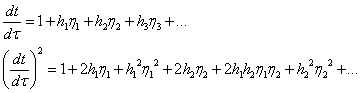
边界条件改写为：

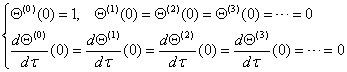
控制方程改写为：

即：

左边：

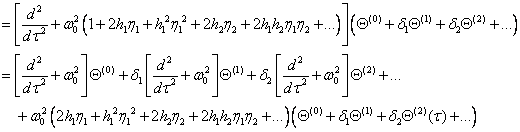
右边：

左右两边比较：

左边含的项的系数必须为零，因为右边最大项为

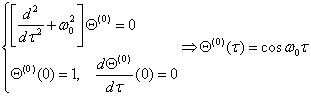
如果，此时必须取，(否则易见)：

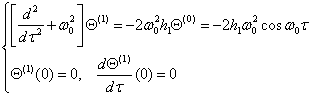
为了消除久期项，必须取，此时还是有(习题P.63Ex.7已经解决)

因此和对应于自变量和因变量中的项可以不取。

那么，为了保证能够消除久期项，必须取

取即可消除久期项。(习题P.63Ex.6已经解决)

类似的方法可以继续讨论下去，将全部定出。

有了上述一般推导过程的结论，所以书上有了一些简单的设定，那么重新写一下：

庞加莱表示：

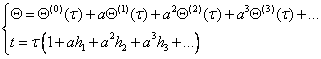
边界条件改写为：

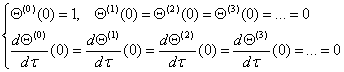
控制方程改写为：

即：

左边：

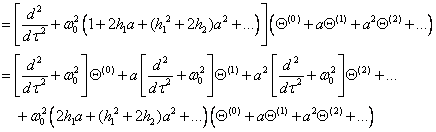
右边：

左右两边比较：

左边含的项的系数必须为零：

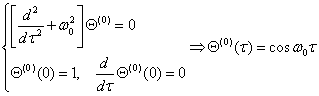
左右两边含的项的系数必须相等：

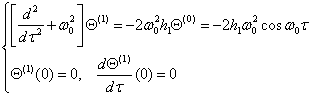
为了消除久期项，必须取，此时还是有(习题P.63Ex.7已经解决)

左右两边含的项的系数必须相等：

取即可消除久期项。(习题P.63Ex.6已经解决)

类似的方法可以继续讨论下去，将全部定出。