P.236 Ex. 12 Buckingham pi theorem
(a) 假设系统有n个基本量![]() 和m个测量量
和m个测量量![]()
在一组基本单位![]() 下,测量值
下,测量值![]() ,其中
,其中![]() 为数值
为数值
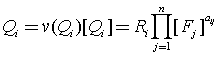
在另一组单位![]() 下,测量值
下,测量值![]() ,其中
,其中![]() 为数值
为数值
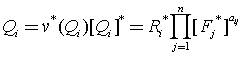
考虑到,从旧单位制到新单位制下每个单位分别缩小![]() 倍,即
倍,即![]() ,
,
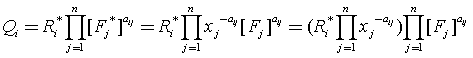
因此:![]() ,即
,即![]()
因为关联测量值的函数关系
![]() (1)
(1)
是完全的,我们有![]() ,所以:
,所以:
![]() (2)
(2)
(b) 将(2)式对![]() 求偏导数:
求偏导数:
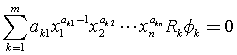
式中,![]() 的下标
的下标![]() 表示对第
表示对第![]() 个变量的偏导数。
个变量的偏导数。
取![]() ,我们有:
,我们有:
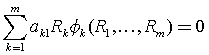 (3)
(3)
(c) 假设![]() ,引进新的自变量
,引进新的自变量![]() :
:
![]() , (4)
, (4)
因此:
![]() , (5)
, (5)
式中:
![]() , (6)
, (6)
则有:
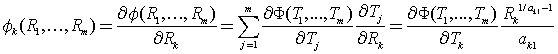
即:
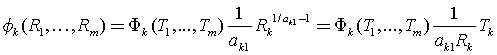
代入(3)式,我们有:
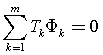 , (7)
, (7)
式中,![]() 的下标
的下标![]() 表示对第
表示对第![]() 个变量的偏导数。
个变量的偏导数。
由
![]()
可见对于第一个基本量来说,所有的量![]() 具有的量纲指数为1。
具有的量纲指数为1。
(d) 引进另一组新的自变量![]() :
:
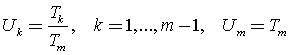 , (8)
, (8)
即
![]()
所以
![]()
因而
![]() , (9)
, (9)
式中,![]() 。 (10)
。 (10)
则有:
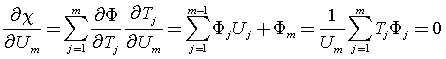
由
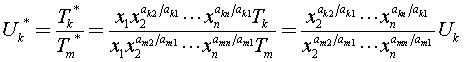
可见对于第一个基本量来说,所有的量![]() 是无量纲的。
是无量纲的。
即,(9)式中包含m-1个对于第一个基本量的量纲指数为0的自变量和1个对于第一个自变量的量纲指数为1的自变量。
(e) 若某些或全部![]() 都为零。
都为零。
不妨设第p个为零,即![]() 。
。
对于(c),我们取![]() ,其他
,其他![]() 不变,那么
不变,那么
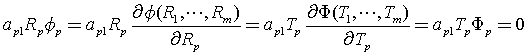
对于(3)式,因为![]() ,所以第p项为零。因此(7)改写为,即
,所以第p项为零。因此(7)改写为,即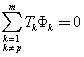 。
。
对于(d),我们取![]() ,其他
,其他![]() 不变。
不变。
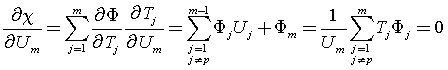
对于有更多![]() 的为零,只要做上述修改即可。
的为零,只要做上述修改即可。
若![]() ,我们任意在
,我们任意在![]() 中取一个不为零的来代替(d)中相应运算即可。
中取一个不为零的来代替(d)中相应运算即可。
如果全部![]() 都为零,那么意味着第1个基本量不在系统中出现,亦即系统可以少一个基本量,我们把这个基本量从系统中去掉,从(a)重新分析问题即可。
都为零,那么意味着第1个基本量不在系统中出现,亦即系统可以少一个基本量,我们把这个基本量从系统中去掉,从(a)重新分析问题即可。
(f)
如上![]() ,亦即
,亦即![]() 与
与![]() 无关,那么
无关,那么![]() 的自变量
的自变量![]() 可以去掉,我们改写成
可以去掉,我们改写成![]() ,即有
,即有![]() 。
。
因为![]() 对于第一个基本量的量纲指数为0,所以类似的我们重复上面的步骤直到第n次,此时我们仍有m-n个自变量
对于第一个基本量的量纲指数为0,所以类似的我们重复上面的步骤直到第n次,此时我们仍有m-n个自变量![]() ,这些变量对于n个基本量的量纲指数均为0,亦即它们是由
,这些变量对于n个基本量的量纲指数均为0,亦即它们是由![]() 的幂次组成的无量纲参数。而和这m-n个自变量关联的方程为:
的幂次组成的无量纲参数。而和这m-n个自变量关联的方程为:
![]() , (11)
, (11)
@USTC© Created by Zhijun Zheng in 2005. Revised by Zhijun Zheng on Dec. 8, 2006.