P92   (3)式的推导

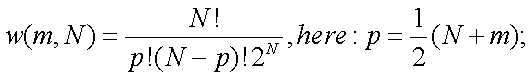
Stirling 公式：

代入

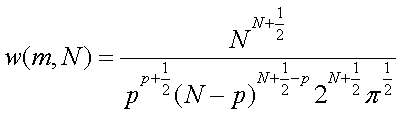
将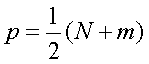代入上式：

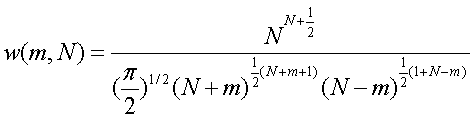
由高数特殊极限P62,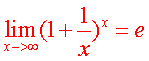

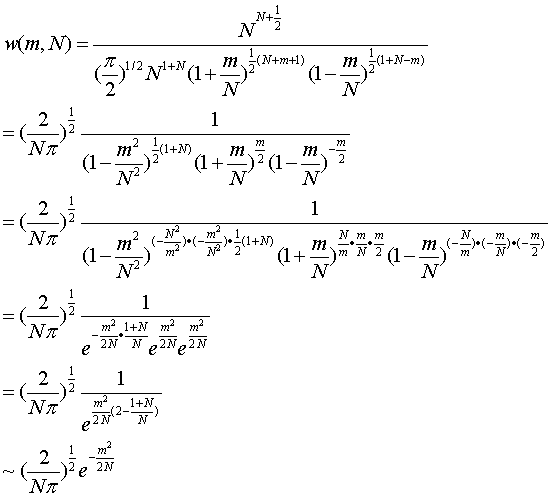
即：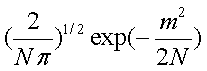

 

附注：（由蒋兴凯同学提供）

应用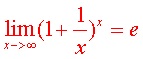 该极限时的形式不同情况：

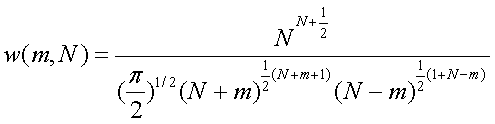
该式直接组织极限形式

 

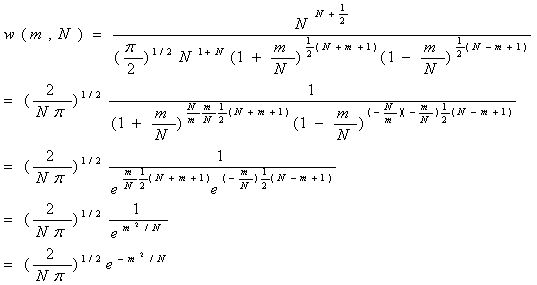
这种推导是没错的。（这个观点是不对的，2011年的课堂解答了这个问题。——zjzheng注，20110929）

解释：

1）第一种推导是为了跟书中一致，所以做了相关组合变换。最后应用了N趋向无穷的条件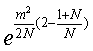，这个式子近似为，这里应用了近似，而第二种推导并未用到近似。那么哪种是正确的？

2） 由于stiring公式就是近似，所以应用该公式得到的结果也为近似。所以书中最后是以~符号的。

3）书中形式对于m，N适中的值时，近似结果与精确式吻合的也很好。参考书中表格。而如果用第二种推导的话，那么m，N适中的值时，近似式与精确式差别较大。比如m=2，4时，近似式分别为0.16及0.05，那么与对应的精确值0.20508和0.11715差别甚远！故书中式子更能兼容更广范围内的参数。

4）对于N, m无穷大情况，和是没有差别的。（这个观点是不对的，2011年的课堂解答了这个问题。——zjzheng注，20110929）

 

附注的附注(20110929)：

事实上，第二种方法中使用了一个近似

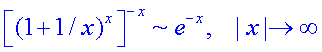
这个近似的精度不够，导致第二种方法的结果与第一种方法出现偏差。如果使用下面的近似就可以顺利的得到第一种方法的结果。

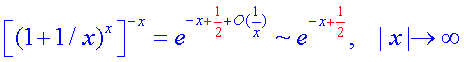
请自行思考第一种方法中为什么不会出现精度不够的问题。