(the nth Catalan number) by using the Taylor expansion of  around x = 0. (If you wish, instead of using the Taylor expansion, you may use the generalization of the binomial expansion (6.5) to non-integral exponents n, where for any real number n and integer k, we interpret
around x = 0. (If you wish, instead of using the Taylor expansion, you may use the generalization of the binomial expansion (6.5) to non-integral exponents n, where for any real number n and integer k, we interpret  to be n(n - 1) . . . (n - k + 1)/k! if k
to be n(n - 1) . . . (n - k + 1)/k! if k  0, and 0 otherwise.)
0, and 0 otherwise.)
d. Show that

Chapter notes
Knuth [123] contains a good discussion of simple binary search trees as well as many variations. Binary search trees seem to have been independently discovered by a number of people in the late 1950's.
Go to Chapter 14 Back to Table of Contents
 (lg n) worst-case time. If the tree is a linear chain of n nodes, however, the same operations take
(lg n) worst-case time. If the tree is a linear chain of n nodes, however, the same operations take  (n) worst-case time. We shall see in Section 13.4 that the height of a randomly built binary search tree is O(lg n), so that basic dynamic-set operations take
(n) worst-case time. We shall see in Section 13.4 that the height of a randomly built binary search tree is O(lg n), so that basic dynamic-set operations take  (lg n) time.
(lg n) time.


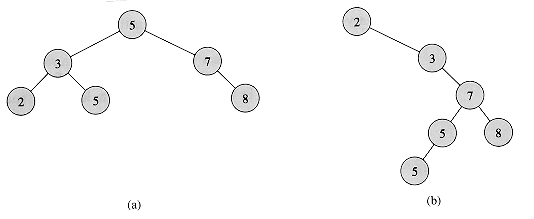
 key[x]. If y is a node in the right subtree of x, then key[x]
key[x]. If y is a node in the right subtree of x, then key[x]  NIL
NIL (n lg n) time in the worst case in the comparison model, any comparison-based algorithm for constructing a binary search tree from an arbitrary list of n elements takes
(n lg n) time in the worst case in the comparison model, any comparison-based algorithm for constructing a binary search tree from an arbitrary list of n elements takes 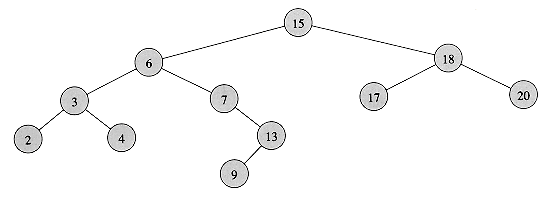
 6
6  left[x]
left[x] A, b
A, b 
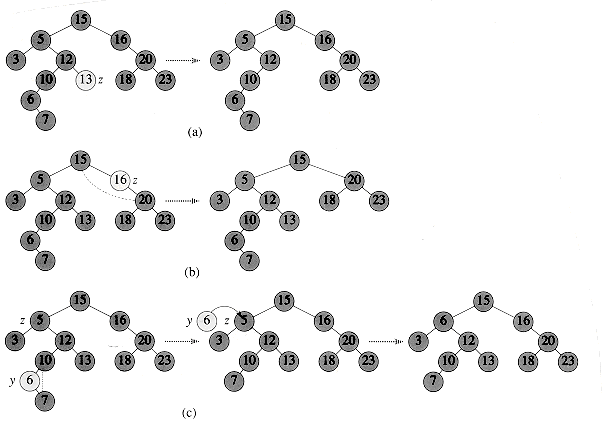
 If y has other fields, copy them, too.
If y has other fields, copy them, too. : Suppose that ki is an ancestor of kj. Consider the tree Ti that results after the keys k1, k2, . . . , ki have been inserted. The path in Ti from the root to ki is the same as the path in T from the root to ki. Thus, if kj were inserted into Ti, it would become either the left or the right child of ki. Consequently (see Exercise 13.2-6), ki is either the smallest key among k1, k2, . . . , ki that is larger than kj or the largest key among k1, k2, . . . , ki that is smaller than kj.
: Suppose that ki is an ancestor of kj. Consider the tree Ti that results after the keys k1, k2, . . . , ki have been inserted. The path in Ti from the root to ki is the same as the path in T from the root to ki. Thus, if kj were inserted into Ti, it would become either the left or the right child of ki. Consequently (see Exercise 13.2-6), ki is either the smallest key among k1, k2, . . . , ki that is larger than kj or the largest key among k1, k2, . . . , ki that is smaller than kj. : Suppose that ki is the smallest key among k1, k2, . . . , ki that is larger than kj. (The case in which ki is the largest key among k1, k2, . . . , ki that is smaller than kj is handled symmetrically.) Comparing kj to any of the keys on the path in T from the root to ki yields the same results as comparing ki to the keys. Hence, when kj is inserted, it follows a path through ki and is inserted as a descendant of ki.
: Suppose that ki is the smallest key among k1, k2, . . . , ki that is larger than kj. (The case in which ki is the largest key among k1, k2, . . . , ki that is smaller than kj is handled symmetrically.) Comparing kj to any of the keys on the path in T from the root to ki yields the same results as comparing ki to the keys. Hence, when kj is inserted, it follows a path through ki and is inserted as a descendant of ki.  Lj, and the depth in T of any key kj is
Lj, and the depth in T of any key kj is
 (
( + 1)Hn}
+ 1)Hn}  4.32 satisfies the equation (ln
4.32 satisfies the equation (ln  = Hn
= Hn 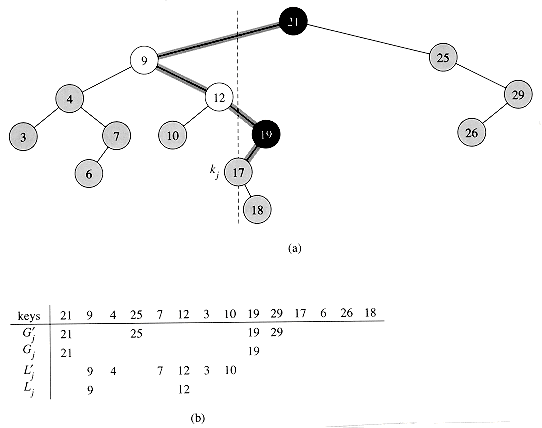










 around x = 0. (If you wish, instead of using the Taylor expansion, you may use the generalization of the binomial expansion (6.5) to non-integral exponents n, where for any real number n and integer k, we interpret
around x = 0. (If you wish, instead of using the Taylor expansion, you may use the generalization of the binomial expansion (6.5) to non-integral exponents n, where for any real number n and integer k, we interpret  to be n(n - 1) . . . (n - k + 1)/k! if k
to be n(n - 1) . . . (n - k + 1)/k! if k 