 (n) time in the worst case--in practice, hashing performs extremely well. Under reasonable assumptions, the expected time to search for an element in a hash table is O(1).
(n) time in the worst case--in practice, hashing performs extremely well. Under reasonable assumptions, the expected time to search for an element in a hash table is O(1).A hash table is a generalization of the simpler notion of an ordinary array. Directly addressing into an ordinary array makes effective use of our ability to examine an arbitrary position in an array in O (1) time. Section 12.1 discusses direct addressing in more detail. Direct addressing is applicable when we can afford to allocate an array that has one position for every possible key.
When the number of keys actually stored is small relative to the total number of possible keys, hash tables become an effective alternative to directly addressing an array, since a hash table typically uses an array of size proportional to the number of keys actually stored. Instead of using the key as an array index directly, the array index is computed from the key. Section 12.2 presents the main ideas, and Section 12.3 describes how array indices can be computed from keys using hash functions. Several variations on the basic theme are presented and analyzed; the "bottom line" is that hashing is an extremely effective and practical technique: the basic dictionary operations require only O (1) time on the average.
12.1 Direct-address tables
Direct addressing is a simple technique that works well when the universe U of keys is reasonably small. Suppose that an application needs a dynamic set in which each element has a key drawn from the universe U = {0,1, . . . , m - 1}, where m is not too large. We shall assume that no two elements have the same key.
To represent the dynamic set, we use an array, or direct-address table, T [0 . . m - 1], in which each position, or slot, corresponds to a key in the universe U. Figure 12.1 illustrates the approach; slot k points to an element in the set with key k. If the set contains no element with key k, then T[k] = NIL.
The dictionary operations are trivial to implement.
Each of these operations is fast: only O(1) time is required.
For some applications, the elements in the dynamic set can be stored in the direct-address table itself. That is, rather than storing an element's key and satellite data in an object external to the direct-address table, with a pointer from a slot in the table to the object, we can store the object in the slot itself, thus saving space. Moreover, it is often unnecessary to store the key field of the object, since if we have the index of an object in the table, we have its key. If keys are not stored, however, we must have some way to tell if the slot is empty.
12.1-1
Consider a dynamic set S that is represented by a direct-address table T of length m. Describe a procedure that finds the maximum element of S. What is the worst-case performance of your procedure?
12.1-2
A bit vector is simply an array of bits (0's and 1's). A bit vector of length m takes much less space than an array of m pointers. Describe how to use a bit vector to represent a dynamic set of distinct elements with no satellite data. Dictionary operations should run in O(1) time.
12.1-3
Suggest how to implement a direct-address table in which the keys of stored elements do not need to be distinct and the elements can have satellite data. All three dictionary operations (INSERT, DELETE, and SEARCH) should run in O(1) time. (Don't forget that DELETE takes as an argument a pointer to an object to be deleted, not a key.)
12.1-4
We wish to implement a dictionary by using direct addressing on a huge array. At the start, the array entries may contain garbage, and initializing the entire array is impractical because of its size. Describe a scheme for implementing a direct-address dictionary on a huge array. Each stored object should use O(1) space; the operations SEARCH, INSERT, and DELETE should take O(1) time each; and the initialization of the data structure should take O(1) time. (Hint: Use an additional stack, whose size is the number of keys actually stored in the dictionary, to help determine whether a given entry in the huge array is valid or not.)
The difficulty with direct addressing is obvious: if the universe U is large, storing a table T of size |U| may be impractical, or even impossible, given the memory available on a typical computer. Furthermore, the set K of keys actually stored may be so small relative to U that most of the space allocated for T would be wasted.
When the set K of keys stored in a dictionary is much smaller than the universe U of all possible keys, a hash table requires much less storage than a direct-address table. Specifically, the storage requirements can be reduced to
With direct addressing, an element with key k is stored in slot k. With hashing, this element is stored in slot h(k); that is, a hash function h is used to compute the slot from the key k. Here h maps the universe U of keys into the slots of a hash table T[0 . . m - 1]:
We say that an element with key k hashes to slot h(k); we also say that h(k) is the hash value of key k. Figure 12.2 illustrates the basic idea. The point of the hash function is to reduce the range of array indices that need to be handled. Instead of |U| values, we need to handle only m values. Storage requirements are correspondingly reduced.
The fly in the ointment of this beautiful idea is that two keys may hash to the same slot--a collision. Fortunately, there are effective techniques for resolving the conflict created by collisions.
Of course, the ideal solution would be to avoid collisions altogether. We might try to achieve this goal by choosing a suitable hash function h. One idea is to make h appear to be "random," thus avoiding collisions or at least minimizing their number. The very term "to hash," evoking images of random mixing and chopping, captures the spirit of this approach. (Of course, a hash function h must be deterministic in that a given input k should always produce the same output h(k).) Since |U| > m, however, there must be two keys that have the same hash value; avoiding collisions altogether is therefore impossible. Thus, while a well-designed, "random"- looking hash function can minimize the number of collisions, we still need a method for resolving the collisions that do occur.
The remainder of this section presents the simplest collision resolution technique, called chaining. Section 12.4 introduces an alternative method for resolving collisions, called open addressing.
In chaining, we put all the elements that hash to the same slot in a linked list, as shown in Figure 12.3. Slot j contains a pointer to the head of the list of all stored elements that hash to j; if there are no such elements, slot j contains NIL.
The dictionary operations on a hash table T are easy to implement when collisions are resolved by chaining.
The worst-case running time for insertion is O(1). For searching, the worst-case running time is proportional to the length of the list; we shall analyze this more closely below. Deletion of an element x can be accomplished in O(1) time if the lists are doubly linked. (If the lists are singly linked, we must first find x in the list T[h(key[x])], so that the next link of x's predecessor can be properly set to splice x out; in this case, deletion and searching have essentially the same running time.)
How well does hashing with chaining perform? In particular, how long does it take to search for an element with a given key?
Given a hash table T with m slots that stores n elements, we define the load factor
The worst-case behavior of hashing with chaining is terrible: all n keys hash to the same slot, creating a list of length n. The worst-case time for searching is thus
The average performance of hashing depends on how well the hash function h distributes the set of keys to be stored among the m slots, on the average. Section 12.3 discusses these issues, but for now we shall assume that any given element is equally likely to hash into any of the m slots, independently of where any other element has hashed to. We call this the assumption of simple uniform hashing.
We assume that the hash value h(k) can be computed in O(1) time, so that the time required to search for an element with key k depends linearly on the length of the list T[h(k)]. Setting aside the O(1) time required to compute the hash function and access slot h(k), let us consider the expected number of elements examined by the search algorithm, that is, the number of elements in the list T[h(k)] that are checked to see if their keys are equal to k. We shall consider two cases. In the first, the search is unsuccessful: no element in the table has key k. In the second, the search successfully finds an element with key k.
Theorem 12.1
In a hash table in which collisions are resolved by chaining, an unsuccessful search takes time
Proof Under the assumption of simple uniform hashing, any key k is equally likely to hash to any of the m slots. The average time to search unsuccessfully for a key k is thus the average time to search to the end of one of the m lists. The average length of such a list is the load factor
Theorem 12.2
In a hash table in which collisions are resolved by chaining, a successful search takes time
Proof We assume that the key being searched for is equally likely to be any of the n keys stored in the table. We also assume that the CHAINED-HASH-INSERT procedure inserts a new element at the end of the list instead of the front. (By Exercise 12.2-3, the average successful search time is the same whether new elements are inserted at the front of the list or at the end.) The expected number of elements examined during a successful search is 1 more than the number of elements examined when the sought-for element was inserted (since every new element goes at the end of the list). To find the expected number of elements examined, we therefore take the average, over the n items in the table, of 1 plus the expected length of the list to which the ith element is added. The expected length of that list is (i- 1)/m, and so the expected number of elements examined in a successful search is
Thus, the total time required for a successful search (including the time for computing the hash function) is
What does this analysis mean? If the number of hash-table slots is at least proportional to the number of elements in the table, we have n = O(m) and, consequently,
12.2-1
Suppose we use a random hash function h to hash n distinct keys into an array T of length m. What is the expected number of collisions? More precisely, what is the expected cardinality of {(x,y): h(x) = h(y)}?
12.2-2
Demonstrate the insertion of the keys 5, 28, 19, 15, 20, 33, 12, 17, 10 into a hash table with collisions resolved by chaining. Let the table have 9 slots, and let the hash function be h(k) = k mod 9.
12.2-3
Argue that the expected time for a successful search with chaining is the same whether new elements are inserted at the front or at the end of a list. (Hint: Show that the expected successful search time is the same for any two orderings of any list.)
12.2-4
Professor Marley hypothesizes that substantial performance gains can be obtained if we modify the chaining scheme so that each list is kept in sorted order. How does the professor's modification affect the running time for successful searches, unsuccessful searches, insertions, and deletions?
12.2-5
Suggest how storage for elements can be allocated and deallocated within the hash table itself by linking all unused slots into a free list. Assume that one slot can store a flag and either one element plus a pointer or two pointers. All dictionary and free-list operations should run in O(l) expected time. Does the free list need to be doubly linked, or does a singly linked free list suffice?
12.2-6
Show that if |U| > nm, there is a subset of U of size n consisting of keys that all hash to the same slot, so that the worst-case searching time for hashing with chaining is
In this section, we discuss some issues regarding the design of good hash functions and then present three schemes for their creation: hashing by division, hashing by multiplication, and universal hashing.
A good hash function satisfies (approximately) the assumption of simple uniform hashing: each key is equally likely to hash to any of the m slots. More formally, let us assume that each key is drawn independently from U according to a probability distribution P; that is, P(k) is the probability that k is drawn. Then the assumption of simple uniform hashing is that
Unfortunately, it is generally not possible to check this condition, since P is usually unknown.
Sometimes (rarely) we do know the distribution P. For example, suppose the keys are known to be random real numbers k independently and uniformly distributed in the range 0
can be shown to satisfy equation (12.1).
In practice, heuristic techniques can be used to create a hash function that is likely to perform well. Qualitative information about P is sometimes useful in this design process. For example, consider a compiler's symbol table, in which the keys are arbitrary character strings representing identifiers in a program. It is common for closely related symbols, such as pt and pts, to occur in the same program. A good hash function would minimize the chance that such variants hash to the same slot.
A common approach is to derive the hash value in a way that is expected to be independent of any patterns that might exist in the data. For example, the "division method" (discussed further below) computes the hash value as the remainder when the key is divided by a specified prime number. Unless that prime is somehow related to patterns in the probability distribution P, this method gives good results.
Finally, we note that some applications of hash functions might require stronger properties than are provided by simple uniform hashing. For example, we might want keys that are "close" in some sense to yield hash values that are far apart. (This property is especially desirable when we are using linear probing, defined in Section 12.4.)
Most hash functions assume that the universe of keys is the set N = {0,1,2, . . .} of natural numbers. Thus, if the keys are not natural numbers, a way must be found to interpret them as natural numbers. For example, a key that is a character string can be interpreted as an integer expressed in suitable radix notation. Thus, the identifier pt might be interpreted as the pair of decimal integers (112,116), since p = 112 and t = 116 in the ASCII character set; then, expressed as a radix-128 integer, pt becomes (112
In the division method for creating hash functions, we map a key k into one of m slots by taking the remainder of k divided by m. That is, the hash function is
For example, if the hash table has size m = 12 and the key is k = 100, then h(k) = 4. Since it requires only a single division operation, hashing by division is quite fast.
When using the division method, we usually avoid certain values of m. For example, m should not be a power of 2, since if m = 2p, then h(k) is just the p lowest-order bits of k. Unless it is known a priori that the probability distribution on keys makes all low-order p-bit patterns equally likely, it is better to make the hash function depend on all the bits of the key. Powers of 10 should be avoided if the application deals with decimal numbers as keys, since then the hash function does not depend on all the decimal digits of k. Finally, it can be shown that when m = 2p - 1 and k is a character string interpreted in radix 2p, two strings that are identical except for a transposition of two adjacent characters will hash to the same value.
Good values for m are primes not too close to exact powers of 2. For example, suppose we wish to allocate a hash table, with collisions resolved by chaining, to hold roughly n = 2000 character strings, where a character has 8 bits. We don't mind examining an average of 3 elements in an unsuccessful search, so we allocate a hash table of size m = 701. The number 701 is chosen because it is a prime near
As a precautionary measure, we could check how evenly this hash function distributes sets of keys among the slots, where the keys are chosen from "real" data.
The multiplication method for creating hash functions operates in two steps. First, we multiply the key k by a constant A in the range 0 < A < 1 and extract the fractional part of kA. Then, we multiply this value by m and take the floor of the result. In short, the hash function is
where "k A mod 1" means the fractional part of kA, that is, kA -
An advantage of the multiplication method is that the value of m is not critical. We typically choose it to be a power of 2--m = 2p for someinteger p--since we can then easily implement the function on most computers as follows. Suppose that the word size of the machine is w bits and that k fits into a single word. Referring to Figure 12.4, we first multiply k by the w-bit integer
Although this method works with any value of the constant A, it works better with some values than with others. The optimal choice depends on the characteristics of the data being hashed. Knuth [123] discusses the choice of A in some detail and suggests that
is likely to work reasonably well.
As an example, if we have k = 123456, m = 10000, and A as in equation (12.2), then
If a malicious adversary chooses the keys to be hashed, then he can choose n keys that all hash to the same slot, yielding an average retrieval time of
The main idea behind universal hashing is to select the hash function at random at run time from a carefully designed class of functions. As in the case of quicksort, randomization guarantees that no single input will always evoke worst-case behavior. Because of the randomization, the algorithm can behave differently on each execution, even for the same input. This approach guarantees good average-case performance, no matter what keys are provided as input. Returning to the example of a compiler's symbol table, we find that the programmer's choice of identifiers cannot now cause consistently poor hashing performance. Poor performance occurs only if the compiler chooses a random hash function that causes the set of identifiers to hash poorly, but the probability of this occurring is small and is the same for any set of identifiers of the same size.
Let
The following theorem shows that a universal class of hash functions gives good average-case behavior.
Theorem 12.3
If h is chosen from a universal collection of hash functions and is used to hash n keys into a table of size m, where n
Proof For each pair y, z of distinct keys, let cyz be a random variable that is 1 if h(y) = h(z) (i.e., if y and z collide using h) and 0 otherwise. Since, by definition, a single pair of keys collides with probability 1/m, we have
Let Cx be the total number of collisions involving key x in a hash table T of size m containing n keys. Equation (6.24) gives
Since n
But how easy is it to design a universal class of hash functions? It is quite easy, as a little number theory will help us prove. Let us choose our table size m to be prime (as in the division method). We decompose a key x into r+ 1 bytes (i.e., characters, or fixed-width binary substrings), so that x =
With this definition,
has mr+1 members.
Theorem 12.4
The class
Proof Consider any pair of distinct keys x, y. Assume that x0
To see this property, note that since m is prime, the nonzero quantity x0 - y0 has a multiplicative inverse modulo m, and thus there is a unique solution for a0 modulo m. (See Section 33.4.) Therefore, each pair of keys x and y collides for exactly mr values of a, since they collide exactly once for each possible value of
12.3-1
Suppose we wish to search a linked list of length n, where each element contains a key k along with a hash value h(k). Each key is a long character string. How might we take advantage of the hash values when searching the list for an element with a given key?
12.3-2
Suppose a string of r characters is hashed into m slots by treating it as a radix-128 number and then using the division method. The number m is easily represented as a 32-bit computer word, but the string of r characters, treated as a radix-128 number, takes many words. How can we apply the division method to compute the hash value of the character string without using more than a constant number of words of storage outside the string itself?
12.3-3
Consider a version of the division method in which h(k) = k mod m, where m = 2p - I and k is a character string interpreted in radix 2p. Show that if string x can be derived from string y by permuting its characters, then x and y hash to the same value. Give an example of an application in which this property would be undesirable in a hash function.
12.3-4
Consider a hash table of size m = 1000 and the hash function h(k) =
12.3-5
Show that if we restrict each component ai of a in equation (12.3) to be nonzero, then the set
In open addressing, all elements are stored in the hash table itself. That is, each table entry contains either an element of the dynamic set or NIL. When searching for an element, we systematically examine table slots until the desired element is found or it is clear that the element is not in the table. There are no lists and no elements stored outside the table, as there are in chaining. Thus, in open addressing, the hash table can "fill up" so that no further insertions can be made; the load factor
Of course, we could store the linked lists for chaining inside the hash table, in the otherwise unused hash-table slots (see Exercise 12.2-5), but the advantage of open addressing is that it avoids pointers altogether. Instead of following pointers, we compute the sequence of slots to be examined. The extra memory freed by not storing pointers provides the hash table with a larger number of slots for the same amount of memory, potentially yielding fewer collisions and faster retrieval.
To perform insertion using open addressing, we successively examine, or probe, the hash table until we find an empty slot in which to put the key. Instead of being fixed in the order 0, 1, . . . , m - 1 (which requires
With open addressing, we require that for every key k, the probe sequence
be a permutation of
The algorithm for searching for key k probes the same sequence of slots that the insertion algorithm examined when key k was inserted. Therefore, the search can terminate (unsuccessfully) when it finds an empty slot, since k would have been inserted there and not later in its probe sequence. (Note that this argument assumes that keys are not deleted from the hash table.) The procedure HASH-SEARCH takes as input a hash table T and a key k, returning j if slot j is found to contain key k, or NIL if key k is not present in table T.
Deletion from an open-address hash table is difficult. When we delete a key from slot i, we cannot simply mark that slot as empty by storing NIL in it. Doing so might make it impossible to retrieve any key k during whose insertion we had probed slot i and found it occupied. One solution is to mark the slot by storing in it the special value DELETED instead of NIL. We would then modify the procedure HASH-SEARCH so that it keeps on looking when it sees the value DELETED, while HASH-INSERT would treat such a slot as if it were empty so that a new key can be inserted. When we do this, though, the search times are no longer dependent on the load factor
In our analysis, we make the assumption of uniform hashing: we assume that each key considered is equally likely to have any of the m! permutations of {0, 1, . . . , m - 1} as its probe sequence. Uniform hashing generalizes the notion of simple uniform hashing defined earlier to the situation in which the hash function produces not just a single number, but a whole probe sequence. True uniform hashing is difficult to implement, however, and in practice suitable approximations (such as double hashing, defined below) are used.
Three techniques are commonly used to compute the probe sequences required for open addressing: linear probing, quadratic probing, and double hashing. These techniques all guarantee that
Given an ordinary hash function h': U
for i = 0,1,...,m - 1. Given key k, the first slot probed is T[h'(k)]. We next probe slot T[h'(k) + 1], and so on up to slot T[m - 1]. Then we wrap around to slots T[0], T[1], . . . , until we finally probe slot T[h'(k) - 1]. Since the initial probe position determines the entire probe sequence, only m distinct probe sequences are used with linear probing.
Linear probing is easy to implement, but it suffers from a problem known as primary clustering. Long runs of occupied slots build up, increasing the average search time. For example, if we have n = m/2 keys in the table, where every even-indexed slot is occupied and every odd-indexed slot is empty, then the average unsuccessful search takes 1.5 probes. If the first n = m/2 locations are the ones occupied, however, the average number of probes increases to about n/4 = m/8. Clusters are likely to arise, since if an empty slot is preceded by i full slots, then the probability that the empty slot is the next one filled is (i + 1)/m, compared with a probability of 1/m if the preceding slot was empty. Thus, runs of occupied slots tend to get longer, and linear probing is not a very good approximation to uniform hashing.
Quadratic probing uses a hash function of the form
where (as in linear probing) h' is an auxiliary hash function, c1 and c2
Double hashing is one of the best methods available for open addressing because the permutations produced have many of the characteristics of randomly chosen permutations. Double hashing uses a hash function of the form
where h1 and h2 are auxiliary hash functions. The initial position probed is T[h1 (k)]; successive probe positions are offset from previous positions by the amount h2(k), modulo m. Thus, unlike the case of linear or quadratic probing, the probe sequence here depends in two ways upon the key k, since the initial probe position, the offset, or both, may vary. Figure 12.5 gives an example of insertion by double hashing.
The value h2(k) must be relatively prime to the hash-table size m for the entire hash table to be searched. Otherwise, if m and h2(k) have greatest common divisor d > 1 for some key k, then a search for key k would examine only (1/d)th of the hash table. (See Chapter 33.) A convenient way to ensure this condition is to let m be a power of 2 and to design h2 so that it always produces an odd number. Another way is to let m be prime and to design h2 so that it always returns a positive integer less than m. For example, we could choose m prime and let
where m' is chosen to be slightly less than m (say, m - 1 or m - 2). For example, if k = 123456 and m = 701, we have h1(k) = 80 and h2(k) = 257, so the first probe is to position 80, and then every 257th slot (modulo m) is examined until the key is found or every slot is examined.
Double hashing represents an improvement over linear or quadratic probing in that
Our analysis of open addressing, like our analysis of chaining, is expressed in terms of the load factor
We assume that uniform hashing is used. In this idealized scheme, the probe sequence
We now analyze the expected number of probes for hashing with open addressing under the assumption of uniform hashing, beginning with an analysis of the number of probes made in an unsuccessful search.
Theorem 12.5
Given an open-address hash table with load factor
Proof In an unsuccessful search, every probe but the last accesses an occupied slot that does not contain the desired key, and the last slot probed is empty. Let us define
pi = Pr {exactly i probes access occupied slots}
for i = 0, 1, 2, . . . . For i > n, we have pi = 0, since we can find at most n slots already occupied. Thus, the expected number of probes is
To evaluate equation (12.6), we define
qi = Pr {at least i probes access occupied slots}
for i = 0, 1, 2, . . . . We can then use identity (6.28):
What is the value of qi for i
With uniform hashing, a second probe, if necessary, is to one of the remaining m - 1 unprobed slots, n - 1 of which are occupied. We make a second probe only if the first probe accesses an occupied slot; thus,
In general, the ith probe is made only if the first i - 1 probes access occupied slots, and the slot probed is equally likely to be any of the remaining m - i + 1 slots, n - i + 1 of which are occupied. Thus,
for i = 1, 2, . . . , n, since (n - j) / (m - j)
We are now ready to evaluate equation (12.6). Given the assumption that
Equation (12.7) has an intuitive interpretation: one probe is always made, with probability approximately
If
Theorem 12.5 gives us the performance of the HASH-INSERT procedure almost immediately.
Corollary 12.6
Inserting an element into an open-address hash table with load factor
Proof An element is inserted only if there is room in the table, and thus
Computing the expected number of probes for a successful search requires a little more work.
Theorem 12.7
Given an open-address hash table with load factor
assuming uniform hashing and assuming that each key in the table is equally likely to be searched for.
Proof A search for a key k follows the same probe sequence as was followed when the element with key k was inserted. By Corollary 12.6, if k was the (i + 1)st key inserted into the hash table, the expected number of probes made in a search for k is at most 1 / (1 - i/m) = m/(m - i). Averaging over all n keys in the hash table gives us the average number of probes in a successful search:
where Hi =
for a bound on the expected number of probes in a successful search.
If the hash table is half full, the expected number of probes is less than 3.387. If the hash table is 90 percent full, the expected number of probes is less than 3.670.
12.4-1
Consider inserting the keys 10, 22, 31, 4, 15, 28, 17, 88, 59 into a hash table of length m = 11 using open addressing with the primary hash function h'(k) = k mod m. Illustrate the result of inserting these keys using linear probing, using quadratic probing with c1 = 1 and c2 = 3, and using double hashing with h2(k) = 1 + (k mod (m - 1)).
12.4-2
Write pseudocode for HASH-DELETE as outlined in the text, and modify HASH-INSERT and HASH-SEARCH to incorporate the special value DELETED.
12.4-3
Suppose that we use double hashing to resolve collisions; that is, we use the hash function h(k, i) = (h1(k) + ih2(k)) mod m. Show that the probe sequence
12.4-4
Consider an open-address hash table with uniform hashing and a load factor
12.4-5
Suppose that we insert n keys into a hash table of size m using open addressing and uniform hashing. Let p(n, m) be the probability that no collisions occur. Show that p(n, m)
12.4-6
The bound on the harmonic series can be improved to
where
12.4-7
Consider an open-address hash table with a load factor
12-1 Longest-probe bound for hashing
A hash table of size m is used to store n items, with n
a. Assuming uniform hashing, show that for i = 1, 2, . . . , n, the probability that the ith insertion requires strictly more than k probes is at most 2-k.
b. Show that for i = 1, 2, . . ., n, the probability that the ith insertion requires more than 2 lg n probes is at most 1/n2.
Let the random variable Xi denote the number of probes required by the ith insertion. You have shown in part (b) that Pr{Xi >2 1g n}
c. Show that Pr{X > 2 1g n}
d. Show that the expected length of the longest probe sequence is E[X] = O(lg n)
12-2 Searching a static set
You are asked to implement a dynamic set of n elements in which the keys are numbers. The set is static (no INSERT or DELETE operations), and the only operation required is SEARCH. You are given an arbitrary amount of time to preprocess the n elements so that SEARCH operations run quickly.
a. Show that SEARCH can be implemented in O(1g n) worst-case time using no extra storage beyond what is needed to store the elements of the set themselves.
b. Consider implementing the set by open-address hashing on m slots, and assume uniform hashing. What is the minimum amount of extra storage m - n required to make the average performance of an unsuccessful SEARCH operation be at least as good as the bound in part (a)? Your answer should be an asymptotic bound on m - n in terms of n.
12-3 Slot-size bound for chaining
Suppose that we have a hash table with n slots, with collisions resolved by chaining, and suppose that n keys are inserted into the table. Each key is equally likely to be hashed to each slot. Let M be the maximum number of keys in any slot after all the keys have been inserted. Your mission is to prove an O(1g n/1g 1g n) upper bound on E[M], the expected value of M.
a. Argue that the probability Qk that k keys hash to a particular slot is given by
b. Let Pk be the probability that M = k, that is, the probability that the slot containing the most keys contains k keys. Show that Pk
c. Use Stirling's approximation, equation (2.1l), to show that Qk < ek/kk.
d. Show that there exists a constant c > 1 such that Qk0 < 1/n3 for k0 = c lg n/lg lg n. Conclude that Pk0 < 1/n2 for k0 = c lg n/lg lg n.
e. Argue that
Conclude that E [M] = O(lg n/1g 1g n).
12-4 Quadratic probing
Suppose that we are given a key k to search for in a hash table with positions 0, 1, . . . , m - 1, and suppose that we have a hash function h mapping the key space into the set {0, 1, . . . , m - 1}. The search scheme is as follows.
1. Compute the value i
2. Probe in position i for the desired key k. If you find it, or if this position is empty, terminate the search.
3. Set j
Assume that m is a power of 2.
a. Show that this scheme is an instance of the general "quadratic probing" scheme by exhibiting the appropriate constants c1 and c2 for equation (12.5).
b. Prove that this algorithm examines every table position in the worst case.
12-5 k-universal hashing
Let
a. Show that if
b. Show that the class
c. Show that if we modify the definition of
then
Knuth [123] and Gonnet [90] are excellent references for the analysis of hashing algorithms. Knuth credits H. P. Luhn (1953) for inventing hash tables, along with the chaining method for resolving collisions. At about the same time, G. M. Amdahl originated the idea of open addressing.
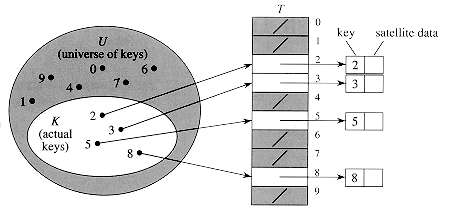
Figure 12.1 Implementing a dynamic set by a direct-address table T. Each key in the universe U = {0,1, . . . , 9} corresponds to an index in the table. The set K = {2, 3, 5, 8} of actual keys determines the slots in the table that contain pointers to elements. The other slots, heavily shaded, contain NIL.
DIRECT-ADDRESS-SEARCH(T,k)
return T[k]
DIRECT-ADDRESS-INSERT(T,x)
T[key[x]]
 x
xDIRECT-ADDRESS-DELETE(T,x)
T[key[x]]
 NIL
NILExercises
12.2 Hash tables
 (|K|), even though searching for an element in the hash table still requires only O(1) time. (The only catch is that this bound is for the average time, whereas for direct addressing it holds for the worst-case time.)
(|K|), even though searching for an element in the hash table still requires only O(1) time. (The only catch is that this bound is for the average time, whereas for direct addressing it holds for the worst-case time.)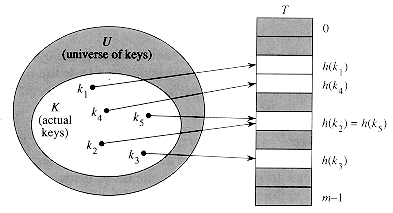
Figure 12.2 Using a hash function h to map keys to hash-table slots. Keys k2 and k5 map to the same slot, so they collide.
h: U
 {0,1, . . . , m - 1} .
{0,1, . . . , m - 1} .
Figure 12.3 Collision resolution by chaining. Each hash-table slot T[j] contains a linked list of all the keys whose hash value is j. For example, h(k1) = h(k4) and h(k5) = h(k2) = h(k7).
Collision resolution by chaining
CHAINED-HASH-INSERT(T,x)
insert x at the head of list T[h(key[x])]
CHAINED-HASH-SEARCH(T,k)
search for an element with key k in list T[h(k)]
CHAINED-HASH-DELETE(T,x)
delete x from the list T[h(key[x])]
Analysis of hashing with chaining
 for T as n/m, that is, the average number of elements stored in a chain. Our analysis will be in terms of
for T as n/m, that is, the average number of elements stored in a chain. Our analysis will be in terms of  ; that is, we imagine
; that is, we imagine  staying fixed as n and m go to infinity. (Note that
staying fixed as n and m go to infinity. (Note that  can be less than, equal to, or greater than l .)
can be less than, equal to, or greater than l .) (n) plus the time to compute the hash function--no better than if we used one linked list for all the elements. Clearly, hash tables are not used for their worst-case performance.
(n) plus the time to compute the hash function--no better than if we used one linked list for all the elements. Clearly, hash tables are not used for their worst-case performance. (1 +
(1 +  ), on the average, under the assumption of simple uniform hashing.
), on the average, under the assumption of simple uniform hashing. = n/m. Thus, the expected number of elements examined in an unsuccessful search is
= n/m. Thus, the expected number of elements examined in an unsuccessful search is  , and the total time required (including the time for computing h(k)) is
, and the total time required (including the time for computing h(k)) is  (1 +
(1 +  ).
).  (1 +
(1 + ), on the average, under the assumption of simple uniform hashing.
), on the average, under the assumption of simple uniform hashing.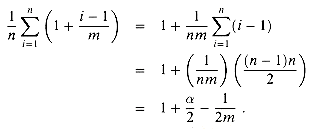
 (2 +
(2 +  /2 - 1/2m) =
/2 - 1/2m) =  (1 +
(1 +  ).
).  = n/m = O(m)/m = O(1). Thus, searching takes constant time on average. Since insertion takes O( l ) worst-case time (see Exercise 12.2-3), and deletion takes O(l) worst-case time when the lists are doubly linked, all dictionary operations can be supported in O( l ) time on average.
= n/m = O(m)/m = O(1). Thus, searching takes constant time on average. Since insertion takes O( l ) worst-case time (see Exercise 12.2-3), and deletion takes O(l) worst-case time when the lists are doubly linked, all dictionary operations can be supported in O( l ) time on average.Exercises
 (n).
(n).12.3 Hash functions
What makes a good hash function?

(12.1)
 k < 1. In this case, the hash function
k < 1. In this case, the hash functionh(k) =
 km
km
Interpreting keys as natural numbers
 128) + 116 = 14452. It is usually straightforward in any given application to devise some such simple method for interpreting each key as a (possibly large) natural number. In what follows, we shall assume that the keys are natural numbers.
128) + 116 = 14452. It is usually straightforward in any given application to devise some such simple method for interpreting each key as a (possibly large) natural number. In what follows, we shall assume that the keys are natural numbers.12.3.1 The division method
h(k) = k mod m .
 = 2000/3 but not near any power of 2. Treating each key k as an integer, our hash function would be
= 2000/3 but not near any power of 2. Treating each key k as an integer, our hash function would beh(k) = k mod 701 .
12.3.2 The multiplication method
h(k) =
 m (k A mod 1)
m (k A mod 1) ,
, kA
kA .
. A
A  2w
2w . The result is a 2w-bit value r1 2w + r0, where r1 is the high-order word of the product and r0 is the low-order word of the product. The desired p-bit hash value consists of the p most significant bits of r0.
. The result is a 2w-bit value r1 2w + r0, where r1 is the high-order word of the product and r0 is the low-order word of the product. The desired p-bit hash value consists of the p most significant bits of r0.
Figure 12.4 The multiplication method of hashing. The w-bit representation of the key k is multiplied by the w-bit value
 A.2w
A.2w , where 0 < A < 1 is a suitable constant. The p highest-order bits of the lower w-bit half of the product form the desired hash value h(k).
, where 0 < A < 1 is a suitable constant. The p highest-order bits of the lower w-bit half of the product form the desired hash value h(k).
(12.2)
h(k) =
 10000
10000  (123456
(123456  0.61803 . . . mod 1)
0.61803 . . . mod 1)
=
 10000
10000  (76300.0041151. . . mod 1)
(76300.0041151. . . mod 1)
=
 10000
10000  0.0041151 . . .
0.0041151 . . .
=
 41.151 . . .
41.151 . . .
= 41 .
12.3.3 Universal hashing
 (n). Any fixed hash function is vulnerable to this sort of worst-case behavior; the only effective way to improve the situation is to choose the hash function randomly in a way that is independent of the keys that are actually going to be stored. This approach, called universal hashing, yields good performance on the average, no matter what keys are chosen by the adversary.
(n). Any fixed hash function is vulnerable to this sort of worst-case behavior; the only effective way to improve the situation is to choose the hash function randomly in a way that is independent of the keys that are actually going to be stored. This approach, called universal hashing, yields good performance on the average, no matter what keys are chosen by the adversary. be a finite collection of hash functions that map a given universe U of keys into the range {0,1, . . . , m - 1}. Such a collection is said to be universal if for each pair of distinct keys x,y
be a finite collection of hash functions that map a given universe U of keys into the range {0,1, . . . , m - 1}. Such a collection is said to be universal if for each pair of distinct keys x,y  U, the number of hash functions
U, the number of hash functions  for which h(x) = h(y) is precisely
for which h(x) = h(y) is precisely  . In other words, with a hash function randomly chosen from
. In other words, with a hash function randomly chosen from  , the chance of a collision between x and y when x
, the chance of a collision between x and y when x  y is exactly 1/m, which is exactly the chance of a collision if h(x) and h(y) are randomly chosen from the set {0,1, . . . , m - 1}.
y is exactly 1/m, which is exactly the chance of a collision if h(x) and h(y) are randomly chosen from the set {0,1, . . . , m - 1}. m, the expected number of collisions involving a particular key x is less than 1.
m, the expected number of collisions involving a particular key x is less than 1.E[cyz] = 1/m .

 m, we have E [Cx] < 1.
m, we have E [Cx] < 1.  x0, x1,. . . , xr
x0, x1,. . . , xr ; the only requirement is that the maximum value of a byte should be less than m. Let a =
; the only requirement is that the maximum value of a byte should be less than m. Let a =  a0, a1, . . . , ar
a0, a1, . . . , ar denote a sequence of r + 1 elements chosen randomly from the set {0,1, . . . , m - 1}. We define a corresponding hash function
denote a sequence of r + 1 elements chosen randomly from the set {0,1, . . . , m - 1}. We define a corresponding hash function  :
:
(12.3)

(12.4)
 defined by equations (12.3) and (12.4) is a universal class of hash functions.
defined by equations (12.3) and (12.4) is a universal class of hash functions. y0. (A similar argument can be made for a difference in any other byte position.) For any fixed values of a1, a2, . . . , ar, there is exactly one value of a0 that satisfies the equation h(x) = h(y); this a0 is the solution to
y0. (A similar argument can be made for a difference in any other byte position.) For any fixed values of a1, a2, . . . , ar, there is exactly one value of a0 that satisfies the equation h(x) = h(y); this a0 is the solution to
 al, a2, . . ., ar
al, a2, . . ., ar (i.e., for the unique value of a0 noted above). Since there are mr+l possible values for the sequence a, keys x and y collide with probability exactly mr/mr+1 = 1/m. Therefore,
(i.e., for the unique value of a0 noted above). Since there are mr+l possible values for the sequence a, keys x and y collide with probability exactly mr/mr+1 = 1/m. Therefore,  is universal.
is universal. Exercises
 m (k A mod 1)
m (k A mod 1) for A =
for A =  . Compute the locations to which the keys 61, 62, 63, 64, and 65 are mapped.
. Compute the locations to which the keys 61, 62, 63, 64, and 65 are mapped. as defined in equation (12.4) is not universal. (Hint: Consider the keys x = 0 and y = 1.)
as defined in equation (12.4) is not universal. (Hint: Consider the keys x = 0 and y = 1.)12.4 Open addressing
 can never exceed 1.
can never exceed 1. (n) search time), the sequence of positions probed depends upon the key being inserted. To determine which slots to probe, we extend the hash function to include the probe number (starting from 0) as a second input. Thus, the hash function becomes
(n) search time), the sequence of positions probed depends upon the key being inserted. To determine which slots to probe, we extend the hash function to include the probe number (starting from 0) as a second input. Thus, the hash function becomesh:U X {0, 1, . . . , m -1}  {0, 1, . . . , m -1} .
{0, 1, . . . , m -1} . h(k, 0), h(k, 1), . . . , h(k, m - 1)
h(k, 0), h(k, 1), . . . , h(k, m - 1)
 0, 1, . . . , m - 1
0, 1, . . . , m - 1 , so that every hash-table position is eventually considered as a slot for a new key as the table fills up. In the following pseudocode, we assume that the elements in the hash table T are keys with no satellite information; the key k is identical to the element containing key k. Each slot contains either a key or NIL (if the slot is empty).
, so that every hash-table position is eventually considered as a slot for a new key as the table fills up. In the following pseudocode, we assume that the elements in the hash table T are keys with no satellite information; the key k is identical to the element containing key k. Each slot contains either a key or NIL (if the slot is empty).HASH-INSERT(T,k)
1 i
 0
02 repeat j
 h(k,i)
h(k,i)3 if T[j] = NIL
4 then T[j]
 k
k5 return j
6 else i
 i + 1
i + 17 until i = m
8 error "hash table overflow"
HASH-SEARCH(T, k)
1 i
 0
02 repeat j
 h(k, i)
h(k, i)3 if T[j]= j
4 then return j
5 i
 i + 1
i + 16 until T[j] = NIL or i = m
7 return NIL
 , and for this reason chaining is more commonly selected as a collision resolution technique when keys must be deleted.
, and for this reason chaining is more commonly selected as a collision resolution technique when keys must be deleted. h(k, 1), h(k, 2), . . . , h(k, m)
h(k, 1), h(k, 2), . . . , h(k, m) is a permutation of
is a permutation of  0, 1, . . . , m - 1
0, 1, . . . , m - 1 for each key k. None of these techniques fulfills the assumption of uniform hashing, however, since none of them is capable of generating more than m2 different probe sequences (instead of the m! that uniform hashing requires). Double hashing has the greatest number of probe sequences and, as one might expect, seems to give the best results.
for each key k. None of these techniques fulfills the assumption of uniform hashing, however, since none of them is capable of generating more than m2 different probe sequences (instead of the m! that uniform hashing requires). Double hashing has the greatest number of probe sequences and, as one might expect, seems to give the best results.Linear probing
 {0, 1, . . . , m - 1}, the method of linear probing uses the hash function
{0, 1, . . . , m - 1}, the method of linear probing uses the hash functionh(k,i) = (h'(k) + i) mod m
Quadratic probing
h(k,i) = (h'(k) + c1i + c2i2) mod m,
(12.5)
 0 are auxiliary constants, and i = 0, 1, . . . , m - 1. The initial position probed is T[h'(k)]; later positions probed are offset by amounts that depend in a quadratic manner on the probe number i. This method works much better than linear probing, but to make full use of the hash table, the values of c1, c2, and m are constrained. Problem 12-4 shows one way to select these parameters. Also, if two keys have the same initial probe position, then their probe sequences are the same, since h(k1, 0) = h(k2, 0) implies h(k1, i) = h(k2, i). This leads to a milder form of clustering, called secondary clustering. As in linear probing, the initial probe determines the entire sequence, so only m distinct probe sequences are used.
0 are auxiliary constants, and i = 0, 1, . . . , m - 1. The initial position probed is T[h'(k)]; later positions probed are offset by amounts that depend in a quadratic manner on the probe number i. This method works much better than linear probing, but to make full use of the hash table, the values of c1, c2, and m are constrained. Problem 12-4 shows one way to select these parameters. Also, if two keys have the same initial probe position, then their probe sequences are the same, since h(k1, 0) = h(k2, 0) implies h(k1, i) = h(k2, i). This leads to a milder form of clustering, called secondary clustering. As in linear probing, the initial probe determines the entire sequence, so only m distinct probe sequences are used.Double hashing
h(k, i) = (h1(k) + ih2(k)) mod m,

Figure 12.5 Insertion by double hashing. Here we have a hash table of size 13 with h1(k) = k mod 13 and h2(k) = 1 + (k mod 11). Since 14
 1 mod 13 and 14
1 mod 13 and 14  3 mod 11, the key 14 will be inserted into empty slot 9, after slots 1 and 5 have been examined and found to be already occupied.
3 mod 11, the key 14 will be inserted into empty slot 9, after slots 1 and 5 have been examined and found to be already occupied.h1(k) = k mod m ,
h2(k) = 1 + (k mod m'),
 (m2) probe sequences are used, rather than
(m2) probe sequences are used, rather than  (m), since each possible (h1 (k), h2(k)) pair yields a distinct probe sequence, and as we vary the key, the initial probe position h1(k) and the offset h2(k) may vary independently. As a result, the performance of double hashing appears to be very close to the performance of the "ideal" scheme of uniform hashing.
(m), since each possible (h1 (k), h2(k)) pair yields a distinct probe sequence, and as we vary the key, the initial probe position h1(k) and the offset h2(k) may vary independently. As a result, the performance of double hashing appears to be very close to the performance of the "ideal" scheme of uniform hashing.Analysis of open-address hashing
 of the hash table, as n and m go to infinity. Recall that if n elements are stored in a table with m slots, the average number of elements per slot is
of the hash table, as n and m go to infinity. Recall that if n elements are stored in a table with m slots, the average number of elements per slot is  = n/m. Of course, with open addressing, we have at most one element per slot, and thus n
= n/m. Of course, with open addressing, we have at most one element per slot, and thus n  m, which implies
m, which implies 
 1.
1. h(k, 0), h(k, 1), . . . , h(k, m - 1)
h(k, 0), h(k, 1), . . . , h(k, m - 1) for each key k is equally likely to be any permutation on
for each key k is equally likely to be any permutation on  0, 1, . . . , m - 1
0, 1, . . . , m - 1 . That is, each possible probe sequence is equally likely to be used as the probe sequence for an insertion or a search. Of course, a given key has a unique fixed probe sequence associated with it; what is meant here is that, considering the probability distribution on the space of keys and the operation of the hash function on the keys, each possible probe sequence is equally likely.
. That is, each possible probe sequence is equally likely to be used as the probe sequence for an insertion or a search. Of course, a given key has a unique fixed probe sequence associated with it; what is meant here is that, considering the probability distribution on the space of keys and the operation of the hash function on the keys, each possible probe sequence is equally likely. = n/m < 1, the expected number of probes in an unsuccessful search is at most 1/(1 -
= n/m < 1, the expected number of probes in an unsuccessful search is at most 1/(1 -  ), assuming uniform hashing.
), assuming uniform hashing.
(12.6)

 1? The probability that the first probe accesses an occupied slot is n/m; thus,
1? The probability that the first probe accesses an occupied slot is n/m; thus,


 n / m if n
n / m if n  m and j
m and j  0. After n probes, all n occupied slots have been seen and will not be probed again, and thus qi = 0 for i
0. After n probes, all n occupied slots have been seen and will not be probed again, and thus qi = 0 for i  n.
n. < 1, the average number of probes in an unsuccessful search is
< 1, the average number of probes in an unsuccessful search is
(12.7)
 a second probe is needed, with probability approximately
a second probe is needed, with probability approximately  2 a third probe is needed, and so on.
2 a third probe is needed, and so on.  is a constant, Theorem 12.5 predicts that an unsuccessful search runs in O(1) time. For example, if the hash table is half full, the average number of probes in an unsuccessful search is 1/(1 - .5) = 2. If it is 90 percent full, the average number of probes is 1/(1 - .9) = 10.
is a constant, Theorem 12.5 predicts that an unsuccessful search runs in O(1) time. For example, if the hash table is half full, the average number of probes in an unsuccessful search is 1/(1 - .5) = 2. If it is 90 percent full, the average number of probes is 1/(1 - .9) = 10. requires at most 1/(1 -
requires at most 1/(1 -  ) probes on average, assuming uniform hashing.
) probes on average, assuming uniform hashing. < 1. Inserting a key requires an unsuccessful search followed by placement of the key in the first empty slot found. Thus, the expected number of probes is 1/(1 -
< 1. Inserting a key requires an unsuccessful search followed by placement of the key in the first empty slot found. Thus, the expected number of probes is 1/(1 -  ).
).  < 1, the expected number of probes in a successful search is at most
< 1, the expected number of probes in a successful search is at most

 is the ith harmonic number (as defined in equation (3.5)). Using the bounds ln i
is the ith harmonic number (as defined in equation (3.5)). Using the bounds ln i  Hi
Hi  ln i + 1 from equations (3.11)and (3.12), we obtain
ln i + 1 from equations (3.11)and (3.12), we obtain
Exercises
 h(k, 0), h(k, 1), . . . , h(k, m - 1)
h(k, 0), h(k, 1), . . . , h(k, m - 1) is a permutation of the slot sequence
is a permutation of the slot sequence  0, 1, . . . , m - 1
0, 1, . . . , m - 1 if and only if h2(k) is relatively prime to m. (Hint: See Chapter 33.)
if and only if h2(k) is relatively prime to m. (Hint: See Chapter 33.) = 1/2. What is the expected number of probes in an unsuccessful search? What is the expected number of probes in a successful search? Repeat these calculations for the load factors 3/4 and 7/8.
= 1/2. What is the expected number of probes in an unsuccessful search? What is the expected number of probes in a successful search? Repeat these calculations for the load factors 3/4 and 7/8. e-n(n - 1)/2m. (Hint: See equation (2.7).) Argue that when n exceeds
e-n(n - 1)/2m. (Hint: See equation (2.7).) Argue that when n exceeds  , the probability of avoiding collisions goes rapidly to zero.
, the probability of avoiding collisions goes rapidly to zero.
(12.8)
 = 0.5772156649 . . . is known as Euler's constant and
= 0.5772156649 . . . is known as Euler's constant and  satisfies 0 <
satisfies 0 <  < 1. (See Knuth [121] for a derivation.) How does this improved approximation for the harmonic series affect the statement and proof of Theorem 12.7?
< 1. (See Knuth [121] for a derivation.) How does this improved approximation for the harmonic series affect the statement and proof of Theorem 12.7? . Find the nonzero value
. Find the nonzero value  for which the expected number of probes in an unsuccessful search equals twice the expected number of probes in a successful search. Use the estimate (1/
for which the expected number of probes in an unsuccessful search equals twice the expected number of probes in a successful search. Use the estimate (1/ ) ln(1/(1 -
) ln(1/(1 -  )) for the number of probes required for a successful search.
)) for the number of probes required for a successful search.Problems
 m/2. Open addressing is used for collision resolution.
m/2. Open addressing is used for collision resolution. 1/n2. Let the random variable X = max1
1/n2. Let the random variable X = max1 i
i n Xi denote the maximum number of probes required by any of the n insertions.
n Xi denote the maximum number of probes required by any of the n insertions. 1/n.
1/n.
 nQk.
nQk.
 h(k), and set j
h(k), and set j  0.
0. (j + l) mod m and i
(j + l) mod m and i  (i + j) mod m, and return to step 2.
(i + j) mod m, and return to step 2. be a class of hash functions in which each h maps the universe U of keys to {0, 1, . . . , m - 1}. We say that
be a class of hash functions in which each h maps the universe U of keys to {0, 1, . . . , m - 1}. We say that  is k-universal if, for every fixed sequence of k distinct keys <x1, x2, . . . , xk> and for any h chosen at random from
is k-universal if, for every fixed sequence of k distinct keys <x1, x2, . . . , xk> and for any h chosen at random from  , the sequence <h(xl), h(x2), . . . , h(xk)> is equally likely to be any of the mk sequences of length k with elements drawn from {0, 1, . . . , m -1}.
, the sequence <h(xl), h(x2), . . . , h(xk)> is equally likely to be any of the mk sequences of length k with elements drawn from {0, 1, . . . , m -1}. is 2-universal, then it is universal.
is 2-universal, then it is universal. defined in Section 12.3.3 is not 2-universal.
defined in Section 12.3.3 is not 2-universal. in Section 12.3.3 so that each function also contains a constant term b, that is, if we replace h(x) with
in Section 12.3.3 so that each function also contains a constant term b, that is, if we replace h(x) withha, b(x)=a
 x + b,
x + b, is 2-universal.
is 2-universal.Chapter notes


