MAKE-HEAP() creates and returns a new heap containing no elements.
INSERT(H, x) inserts node x, whose key field has already been filled in, into heap H.
MINIMUM(H) returns a pointer to the node in heap H whose key is minimum.
EXTRACT-MIN(H) deletes the node from heap H whose key is minimum, returning a pointer to the node.
UNION(Hl, H2) creates and returns a new heap that contains all the nodes of heaps H1 and H2. Heaps H1 and H2 are "destroyed" by this operation.
In addition, the data structures in these chapters also support the following two operations.
DECREASE-KEY(H, x, k) assigns to node x within heap H the new key value k, which is assumed to be no greater than its current key value.
DELETE(H, x) deletes node x from heap H.
As the table in Figure 20.1 shows, if we don't need the UNION operation, ordinary binary heaps, as used in heapsort (Chapter 7), work well. Operations other than UNION run in worst-case time O(lg n) (or better) on a binary heap. If the UNION operation must be supported, however, binary heaps perform poorly. By concatenating the two arrays that hold the binary heaps to be merged and then running HEAPIFY, the UNION operation takes
In this chapter, we shall examine "binomial heaps," whose worst-case time bounds are also shown in Figure 20.1. In particular, the UNION operation takes only O(lg n) time to merge two binomial heaps with a total of n elements.
In Chapter 21, we shall explore Fibonacci heaps, which have even better time bounds for some operations. Note, however, that the running times for Fibonacci heaps in Figure 20.1 are amortized time bounds, not worst-case per operation time bounds.
This chapter ignores issues of allocating nodes prior to insertion and freeing nodes following deletion. We assume that the code that calls the heap procedures handles these details.
Binary heaps, binomial heaps, and Fibonacci heaps are all inefficient in their support of the operation SEARCH; it can take a while to find a node with a given key. For this reason, operations such as DECREASE-KEY and DELETE that refer to a given node require a pointer to that node as part of their input. This requirement poses no problem in many applications.
Section 20.1 defines binomial heaps after first defining their constituent binomial trees. It also introduces a particular representation of binomial heaps. Section 20.2 shows how we can implement operations on binomial heaps in the time bounds given in Figure 20.1.
A binomial heap is a collection of binomial trees, so this section starts by defining binomial trees and proving some key properties. We then define binomial heaps and show how they can be represented.
The binomial tree Bk is an ordered tree (see Section 5.5.2) defined recursively. As shown in Figure 20.2(a), the binomial tree B0 consists of a single node. The binomial tree Bk consists of two binomial trees Bk-1 that are linked together: the root of one is the leftmost child of the root of the other. Figure 20.2(b) shows the binomial trees B0 through B4.
Some properties of binomial trees are given by the following lemma.
Lemma 20.1
For the binomial tree Bk,
1. there are 2k nodes,
2. the height of the tree is k,
3. there are exactly
4. the root has degree k, which is greater than that of any other node; moreover if the children of the root are numbered from left to right by k - 1, k - 2, . . . , 0, child i is the root of a subtree Bi.
Proof The proof is by induction on k. For each property, the basis is the binomial tree B0. Verifying that each property holds for B0 is trivial.
For the inductive step, we assume that the lemma holds for Bk-1.
1. Binomial tree Bk consists of two copies of Bk-1, so Bk has 2k-1 + 2k-1 = 2k nodes.
2. Because of the way in which the two copies of Bk-1 are linked to form Bk, the maximum depth of a node in Bk is one greater than the maximum depth in Bk-1 . By the inductive hypothesis, this maximum depth is (k-1) + 1 = k.
3. Let D(k, i) be the number of nodes at depth i of binomial tree Bk. Since Bk is composed of two copies of Bk-1 linked together, a node at depth i in Bk-1 appears in Bk once at depth i and once at depth i + 1. In other words, the number of nodes at depth i in Bk is the number of nodes at depth i in Bk-1 plus the number of nodes at depth i - 1 in Bk-1 . Thus,
The second equality follows from the inductive hypothesis, and the third equality follows from Exercise 6.1-7.
4. The only node with greater degree in Bk than in Bk-1, is the root, which has one more child than in Bk-1. Since the root of Bk-1 has degree k-1, the root of Bk has degree k. Now by the inductive hypothesis, and as Figure 20.2(c) shows, from left to right, the children of the root of Bk-1 are roots of Bk-2, Bk-3, . . ., B0. When Bk-1 is linked to Bk-1, therefore, the children of the resulting root are roots of Bk-1, Bk-2, . . . , B0
Corollary 20.2
The maximum degree of any node in an n-node binomial tree is lg n.
Proof Immediate from properties l and 4 of Lemma 20.1.
The term "binomial tree" comes from property 3 of Lemma 20.1, since the terms
A binomial heap H is a set of binomial trees that satisfies the following binomial-heap properties.
1. Each binomial tree in H is heap-ordered: the key of a node is greater than or equal to the key of its parent.
2. There is at most one binomial tree in H whose root has a given degree.
The first property tells us that the root of a heap-ordered tree contains the smallest key in the tree.
The second property implies that an n-node binomial heap H consists of at most
Figure 20.3(a) shows a binomial heap H with 13 nodes. The binary representation of 13 is
As shown in Figure 20.3(b), each binomial tree within a binomial heap is stored in the left-child, right-sibling representation of Section 11.4. Each node has a key field and any other satellite information required by the application. In addition, each node x contains pointers p[x] to its parent, child [x] to its leftmost child, and sibling[x] to the sibling of x immediately to its right. If node x is a root, then p[x] = NIL. If node x has no children, then child[x] = NIL, and if x is the rightmost child of its parent, then sibling[x] = NIL. Each node x also contains the field degree[x] , which is the number of children of x.
As Figure 20.3 also shows, the roots of the binomial trees within a binomial heap are organized in a linked list, which we refer to as the root list. The degrees of the roots strictly increase as we traverse the root list. By the second binomial-heap property, in an n-node binomial heap the degrees of the roots are a subset of {0, 1, . . . ,
A given binomial heap H is accessed by the field head[H], which is simply a pointer to the first root in the root list of H. If binomial heap H has no elements, then head[H] = NIL.
20.1-1
Suppose that x is a node in a binomial tree within a binomial heap, and assume that sibling[x]
20.1-2
If x is a nonroot node in a binomial tree within a binomial heap, how does degree[p[x]] compare to degree[x]?
20.1-3
Suppose we label the nodes of binomial tree Bk in binary by a postorder walk, as in Figure 20.4. Consider a node x labeled l at depth i, and let j = k - i. Show that x has j l's in its binary representation. How many binary k-strings are there that contain exactly j 1's? Show that the degree of x is equal to the number of 1's to the right of the rightmost 0 in the binary representation of l.
In this section, we show how to perform operations on binomial heaps in the time bounds shown in Figure 20.1. We shall only show the upper bounds; the lower bounds are left as Exercise 20.2-10.
To make an empty binomial heap, the MAKE-BINOMIAL-HEAP procedure simply allocates and returns an object H, where head[H] = NIL. The running time is
The procedure BINOMIAL-HEAP-MINIMUM returns a pointer to the node with the minimum key in an n-node binomial heap H. This implementation assumes that there are no keys with value
Since a binomial heap is heap-ordered, the minimum key must reside in a root node. The BINOMIAL-HEAP-MINIMUM procedure checks all roots, which number at most
Because there are at most
The operation of uniting two binomial heaps is used as a subroutine by most of the remaining operations. The BINOMIAL-HEAP-UNION procedure repeatedly links binomial trees whose roots have the same degree. The following procedure links the Bk-1 tree rooted at node y to the Bk-1 tree rooted at node z; that is, it makes z the parent of y. Node z thus becomes the root of a Bk tree.
The BINOMIAL-LINK procedure makes node y the new head of the linked list of node z's children in O(1) time. It works because the left-child, right-sibling representation of each binomial tree matches the ordering property of the tree: in a Bk tree, the leftmost child of the root is the root of a Bk-1 tree.
The following procedure unites binomial heaps H1 and H2, returning the resulting heap. It destroys the representations of H1 and H2 in the process. Besides BINOMIAL-LINK, the procedure uses an auxiliary procedure BINOMIAL-HEAP-MERGE that merges the root lists of H1 and H2 into a single linked list that is sorted by degree into monotonically increasing order. The BINOMIAL-HEAP-MERGE procedure, whose pseudocode we leave as Exercise 20.2-2, is similar to the MERGE procedure in Section 1.3.1.
Figure 20.5 shows an example of BINOMIAL-HEAP-UNION in which all four cases given in the pseudocode occur.
The BINOMIAL-HEAP-UNION procedure has two phases. The first phase, performed by the call of BINOMIAL-HEAP-MERGE, merges the root lists of binomial heaps H1 and H2 into a single linked list H that is sorted by degree into monotonically increasing order. There might be as many as two roots (but no more) of each degree, however, so the second phase links roots of equal degree until at most one root remains of each degree. Because the linked list H is sorted by degree, we can perform all the link operations quickly.
In detail, the procedure works as follows. Lines 1-3 start by merging the root lists of binomial heaps H1 and H2 into a single root list H. The root lists of H1 and H2 are sorted by strictly increasing degree, and BINOMIAL-HEAP-MERGE returns a root list H that is sorted by monotonically increasing degree. If the root lists of H1 and H2 have m roots altogether, BINOMIAL-HEAP-MERGE runs in O(m) time by repeatedly examining the roots at the heads of the two root lists and appending the root with the lower degree to the output root list, removing it from its input root list in the process.
The BINOMIAL-HEAP-UNION procedure next initializes some pointers into the root list of H. First, it simply returns in lines 4-5 if it happens to be uniting two empty binomial heaps. From line 6 on, therefore, we know that H has at least one root. Throughout the procedure, we maintain three pointers into the root list:
Initially, there are at most two roots on the root list H of a given degree: because H1 and H2 were binomial heaps, they each had only one root of a given degree. Moreover, BINOMIAL-HEAP-MERGE guarantees us that if two roots in H have the same degree, they are adjacent in the root list.
In fact, during the execution of BINOMlAL-HEAP-UNION, there may be three roots of a given degree appearing on the root list H at some time. We shall see in a moment how this situation could occur. At each iteration of the while loop of lines 9-21, therefore, we decide whether to link x and next-x based on their degrees and possibly the degree of sibling[next-x]. An invariant of the loop is that each time we start the body of the loop, both x and next-x are non-NIL.
Case 1, shown in Figure 20.6(a), occurs when degree[x]
Case 2, shown in Figure 20.6(b), occurs when x is the first of three roots of equal degree, that is, when
We handle this case in the same manner as case 1: we just march the pointers one position further down the list. Line 10 tests for both cases 1 and 2, and lines 11-12 handle both cases.
Cases 3 and 4 occur when x is the first of two roots of equal degree, that is, when
These cases may occur on the next iteration after any case, but one of them always occurs immediately following case 2. In cases 3 and 4, we link x and next-x. The two cases are distinguished by whether x or next-x has the smaller key, which determines the node that will be the root after the two are linked.
In case 3, shown in Figure 20.6(c), key[x]
In case 4, shown in Figure 20.6(d), next-x has the smaller key, so x is linked to next-x. Lines 16-18 remove x from the root list, which has two cases depending on whether x is the first root on the list (line 17) or is not (line 18). Line 19 then makes x the leftmost child of next-x, and line 20 updates x for the next iteration.
Following either case 3 or case 4, the setup for the next iteration of the while loop is the same. We have just linked two Bk-trees to form a Bk+l-tree, which x now points to. There were already zero, one, or two other Bk+1-trees on the root list from the output of BINOMIAL-HEAP-MERGE, so x is now the first of either one, two, or three Bk+l-trees on the root list. If x is the only one, then we enter case 1 in the next iteration: degree [x]
The running time of BINOMIAL-HEAP-UNION is O(1g n), where n is the total number of nodes in binomial heaps H1 and H2. We can see this as follows. Let H1 contain n1 nodes and H2 contain n2 nodes, so that n = n1 + n2. Then, H1 contains at most
The following procedure inserts node x into binomial heap H, assuming of course that node x has already been allocated and key[x] has already been filled in.
The procedure simply makes a one-node binomial heap H' in O(1) time and unites it with the n-node binomial heap H in O(1g n) time. The call to BINOMIAL-HEAP-UNION takes care of freeing the temporary binomial heap H'. (A direct implementation that does not call BINOMIAL-HEAP-UNION is given as Exercise 20.2-8.)
The following procedure extracts the node with the minimum key from binomial heap H and returns a pointer to the extracted node.
This procedure works as shown in Figure 20.7. The input binomial heap H is shown in Figure 20.7(a). Figure 20.7(b) shows the situation after line 1: the root x with the minimum key has been removed from the root list of H. If x is the root of a Bk-tree, then by property 4 of Lemma 20.1, x's children, from left to right, are roots of Bk-1-, Bk-2-, . . . , B0-trees. Figure 20.7(c) shows that by reversing the list of x's children in line 3, we have a binomial heap H' that contains every node in x's tree except for x itself. Because x's tree is removed from H in line 1, the binomial heap that results from uniting H and H' in line 4, shown in Figure 20.7(d), contains all the nodes originally in H except for x. Finally, line 5 returns x.
Since each of lines 1-4 takes O(lg n) time if H has n nodes, BINOMIAL-HEAP-EXTRACT-MIN runs in O(lg n) time.
The following procedure decreases the key of a node x in a binomial heap H to a new value k. It signals an error if k is greater than x's current key.
As shown in Figure 20.8, this procedure decreases a key in the same manner as in a binary heap: by "bubbling up" the key in the heap. After ensuring that the new key is in fact no greater than the current key and then assigning the new key to x, the procedure goes up the tree, with y initially pointing to node x. In each iteration of the while loop of lines 6-10, key[y] is checked against the key of y's parent z. If y is the root or key[y]
The BINOMIAL-HEAP-DECREASE-KEY procedure takes O(lg n) time. By property 2 of Lemma 20.1, the maximum depth of x is
It is easy to delete a node x's key and satellite information from binomial heap H in O(lg n) time. The following implementation assumes that no node currently in the binomial heap has a key of -
The BINOMIAL-HEAP-DELETE procedure makes node x have the unique minimum key in the entire binomial heap by giving it a key of -
The BINOMIAL-HEAP-DELETE procedure takes O(lg n) time.
20.2-1
Give an example of two binary heaps with n elements each such that BUILD-HEAP takes
20.2-2
Write pseudocode for BINOMIAL-HEAP-MERGE.
20.2-3
Show the binomial heap that results when a node with key 24 is inserted into the binomial heap shown in Figure 20.7(d).
20.2-4
Show the binomial heap that results when the node with key 28 is deleted from the binomial heap shown in Figure 20.8(c).
20.2-5
Explain why the BINOMIAL-HEAP-MINIMUM procedure might not work correctly if keys can have the value
20.2-6
Suppose there is no way to represent the key -
20.2-7
Discuss the relationship between inserting into a binomial heap and incrementing a binary number and the relationship between uniting two binomial heaps and adding two binary numbers.
20.2-8
In light of Exercise 20.2-7, rewrite BINOMIAL-HEAP-INSERT to insert a node directly into a binomial heap without calling BINOMIAL-HEAP-UNION.
20.2-9
Show that if root lists are kept in strictly decreasing order by degree (instead of strictly increasing order), each of the binomial heap operations can be implemented without changing its asymptotic running time.
20.2-10
Find inputs that cause BINOMIAL-HEAP-EXTRACT-MIN, BINOMIAL-HEAP-DECREASE-KEY, and BINOMIAL-HEAP-DELETE to run in
20-1 2-3-4 heaps
Chapter 19 introduced the 2-3-4 tree, in which every internal node (other than possibly the root) has two, three, or four children and all leaves have the same depth. In this problem, we shall implement 2-3-4 heaps, which support the mergeable-heap operations.
The 2-3-4 heaps differ from 2-3-4 trees in the following ways. In 2-3-4 heaps, only leaves store keys, and each leaf x stores exactly one key in the field key[x]. There is no particular ordering of the keys in the leaves; that is, from left to right, the keys may be in any order. Each internal node x contains a value small[x] that is equal to the smallest key stored in any leaf in the subtree rooted at x. The root r contains a field height [r] that is the height of the tree. Finally, 2-3-4 heaps are intended to be kept in main memory, so that disk reads and writes are not needed.
Implement the following 2-3-4 heap operations. Each of the operations in parts (a)-(e) should run in O(lg n) time on a 2-3-4 heap with n elements. The UNION operation in part (f) should run in O(lg n) time, where n is the number of elements in the two input heaps.
a. MINIMUM, which returns a pointer to the leaf with the smallest key.
b. DECREASE-KEY, which decreases the key of a given leaf x to a given value k
c. INSERT, which inserts leaf x with key k.
d. DELETE, which deletes a given leaf x.
e. EXTRACT-MIN, which extracts the leaf with the smallest key.
f. UNION, which unites two 2-3-4 heaps, returning a single 2-3-4 heap and destroying the input heaps.
20-2 Minimum-spanning-tree algorithm using mergeable heaps
Chapter 24 presents two algorithms to solve the problem of finding a minimum spanning tree of an undirected graph. Here, we shall see how mergeable heaps can be used to devise a different minimum-spanning-tree algorithm.
We are given a connected, undirected graph G = (V, E) with a weight function w: E
is minimized.
The following pseudocode, which can be proven correct using techniques from Section 24.1, constructs a minimum spanning tree T. It maintains a partition {Vi} of the vertices of V and, with each set Vi, a set
of edges incident on vertices in Vi.
Describe how to implement this algorithm using the mergeable-heap operations given in Figure 20.1. Give the running time of your implementation, assuming that the mergeable heaps are implemented by binomial heaps.
Binomial heaps were introduced in 1978 by Vuillemin [196]. Brown[36, 37] studied their properties in detail.
 (n) time in the worst case.
(n) time in the worst case. Binary heap Binomial heap Fibonacci heap
Procedure (worst-case) (worst-case) (amortized)
--------------------------------------------------------------
MAKE-HEAP
 (1)
(1)  (1)
(1)  (1)
(1)INSERT
 (lg n) O(lg n)
(lg n) O(lg n)  (1)
(1)MINIMUM
 (1) O(lg n)
(1) O(lg n)  (l)
(l)EXTRACT-MIN
 (lg n)
(lg n)  (1g n) O(lg n)
(1g n) O(lg n)UNION
 (n) O(lg n)
(n) O(lg n)  (1)
(1)DECREASE-KEY
 (lg n)
(lg n)  (lg n)
(lg n)  (1)
(1)DELETE
 (1g n)
(1g n)  (lg n) O(lg n)
(lg n) O(lg n)Figure 20.1 Running times for operations on three implementations of mergeable heaps. The number of items in the heap(s) at the time of an operation is denoted by n.
20.1 Binomial trees and binomial heaps
20.1.1 Binomial trees

Figure 20.2 (a) The recursive definition of the binomial tree Bk. Triangles represent rooted subtrees. (b) The binomial trees Bo through B4. Node depths in B4 are shown. (c) Another way of looking at the binomial tree Bk.
 nodes at depth i for i = 0, 1, . . . , k, and
nodes at depth i for i = 0, 1, . . . , k, and
 are the binomial coefficients. Exercise 20.1-3 gives further justification for the term.
are the binomial coefficients. Exercise 20.1-3 gives further justification for the term.20.1.2 Binomial heaps
 lg n
lg n + 1 binomial trees. To see why, observe that the binary representation of n has
+ 1 binomial trees. To see why, observe that the binary representation of n has  lg n
lg n  + 1 bits, say
+ 1 bits, say  b
b lg n
lg n ,b
,b lg n
lg n - 1 , . . . , b0
- 1 , . . . , b0 , so that
, so that  . By property 1 of Lemma 20.1, therefore, binomial tree Bi appears in H if and only if bit bi = 1. Thus, binomial heap H contains at most
. By property 1 of Lemma 20.1, therefore, binomial tree Bi appears in H if and only if bit bi = 1. Thus, binomial heap H contains at most  lg n
lg n + 1 binomial trees.
+ 1 binomial trees.
Figure 20.3 A binomial heap H with n = 13 nodes. (a) The heap consists of binomial trees B0, B2, and B3, which have 1, 4, and 8 nodes respectively, totaling n = 13 nodes. Since each binomial tree is heap-ordered, the key of any node is no less than the key of its parent. Also shown is the root list, which is a linked list of roots in order of increasing degree. (b) A more detailed representation of binomial heap H. Each binomial tree is stored in the left-child, right-sibling representation, and each node stores its degree.
 1101
1101 , and H consists of heap-ordered binomial trees B3, B2, and B0, having 8, 4, and 1 nodes respectively, for a total of 13 nodes.
, and H consists of heap-ordered binomial trees B3, B2, and B0, having 8, 4, and 1 nodes respectively, for a total of 13 nodes.Representing binomial heaps

Figure 20.4 The binomial tree B4 with nodes labeled in binary by a postorder walk.
 1g n
1g n }. The sibling field has a different meaning for roots than for nonroots. If x is a root, then sibling[x] points to the next root in the root list. (As usual, sibling[x] = NIL if x is the last root in the root list.)
}. The sibling field has a different meaning for roots than for nonroots. If x is a root, then sibling[x] points to the next root in the root list. (As usual, sibling[x] = NIL if x is the last root in the root list.)Exercises
 NIL. If x is not a root, how does degree[sibling[x]] compare to degree[x]? How about if x is a root?
NIL. If x is not a root, how does degree[sibling[x]] compare to degree[x]? How about if x is a root?20.2 Operations on binomial heaps
Creating a new binomial heap
 (1).
(1).Finding the minimum key
 . (See Exercise 20.2-5.)
. (See Exercise 20.2-5.)BINOMIAL-HEAP-MINIMUM(H)
1 y
 NIL
NIL2 x
 head[H]
head[H]3 min


4 while x
 NIL
NIL5 do if key[x] < min
6 then min
 key[x]
key[x]7 y
 x
x8 x
 sibling[x]
sibling[x]9 return y
 lg n
lg n + 1, saving the current minimum in min and a pointer to the current minimum in y. When called on the binomial heap of Figure 20.3, BINOMIAL-HEAP-MINIMUM returns a pointer to the node with key 1.
+ 1, saving the current minimum in min and a pointer to the current minimum in y. When called on the binomial heap of Figure 20.3, BINOMIAL-HEAP-MINIMUM returns a pointer to the node with key 1. lg n
lg n + 1 roots to check, the running time of BINOMIAL-HEAP-MINIMUM is O(lg n).
+ 1 roots to check, the running time of BINOMIAL-HEAP-MINIMUM is O(lg n).Uniting two binomial heaps
BINOMIAL-LINK(y,z)
1 p[y]
 z
z2 sibling[y]
 child[z]
child[z]3 child[z]
 y
y4 degree[z]
 degree[z]+1
degree[z]+1
 x points to the root currently being examined,
x points to the root currently being examined, prev-x points to the root preceding x on the root list: sibling[prev-x] = x, and
prev-x points to the root preceding x on the root list: sibling[prev-x] = x, and next-x points to the root following x on the root list: sibling[x] = next-x.
next-x points to the root following x on the root list: sibling[x] = next-x. degree[next-x], that is, when x is the root of a Bk-tree and next-x is the root of a Bl-tree for some l > k. Lines 11-12 handle this case. We don't link x and next-x, so we simply march the pointers one position further down the list. Updating next-x to point to the node following the new node x is handled in line 21, which is common to every case.
degree[next-x], that is, when x is the root of a Bk-tree and next-x is the root of a Bl-tree for some l > k. Lines 11-12 handle this case. We don't link x and next-x, so we simply march the pointers one position further down the list. Updating next-x to point to the node following the new node x is handled in line 21, which is common to every case.degree[x] = degree[next-x] = degree[sibling[next-x]].
degree[x] = degree[next-x]
 degree[sibling[next-x]].
degree[sibling[next-x]]. key[next-x], so next-x is linked to x. Line 14 removes next-x from the root list, and line 15 makes next-x the leftmost child of x.
key[next-x], so next-x is linked to x. Line 14 removes next-x from the root list, and line 15 makes next-x the leftmost child of x.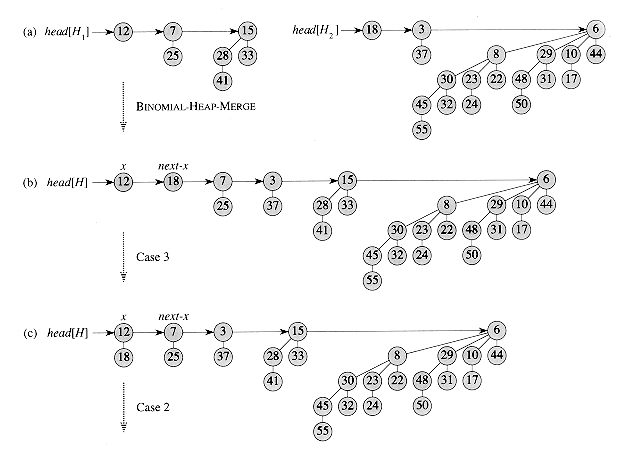
Figure 20.5 The execution of BINOMIAL-HEAP-UNION.(a) Binomial heaps H1 and H2. (b) Binomial heap H is the output of BINOMIAL-HEAP-MERGE(H1,H2). Initially, x is the first root on the root list of H. Because both x and next-x have degree 0 and key[x] < key[next-x], case 3 applies. (c) After the link occurs, x is the first of three roots with the same degree, so case 2 applies. (d) After all the pointers move down one position in the root list, case 4 applies, since x is the first of two roots of equal degree. (e) After the link occurs, case 3 applies. (f) After another link, case 1 applies, because x has degree 3 and next-x has degree 4. This iteration of the while loop is the last, because after the pointers move down one position in the root list, next-x = NIL.

 degree[next-x]. If x is the first of two, then we enter either case 3 or case 4 in the next iteration. It is when x is the first of three that we enter case 2 in the next iteration.
degree[next-x]. If x is the first of two, then we enter either case 3 or case 4 in the next iteration. It is when x is the first of three that we enter case 2 in the next iteration. 1g n1
1g n1 + 1 roots and H2 contains at most
+ 1 roots and H2 contains at most  1g n2
1g n2 + 1 roots, so H contains at most
+ 1 roots, so H contains at most  1g n2
1g n2 +
+  1g n1
1g n1 + 2
+ 2  2
2  1g n
1g n + 2 = O(1g n) roots immediately after the call of BINOMIAL-HEAP-MERGE. The time to perform BINOMIAL-HEAP-MERGE is thus O(lg n). Each iteration of the while loop takes O(1) time, and there are at most
+ 2 = O(1g n) roots immediately after the call of BINOMIAL-HEAP-MERGE. The time to perform BINOMIAL-HEAP-MERGE is thus O(lg n). Each iteration of the while loop takes O(1) time, and there are at most  1g n1
1g n1 +
+  1g n2
1g n2 + 2 iterations because each iteration either advances the pointers one position down the root list of H or removes a root from the root list. The total time is thus O(lg n).
+ 2 iterations because each iteration either advances the pointers one position down the root list of H or removes a root from the root list. The total time is thus O(lg n).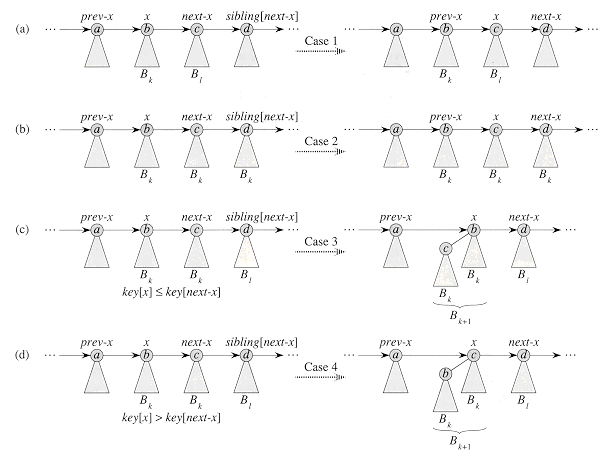
Figure 20.6 The four cases that occur in BINOMIAL-HEAP-UNION. Labels a, b, c, and d serve only to identify the roots involved; they do not indicate the degrees or keys of these roots. In each case, x is the root of a Bk-tree and l > k. (a) Case 1: degree[x]
 degree[next-x]. The pointers move one position further down the root list. (b) Case 2: degree[x] = degree[next-x] = degree[sibling[next-x]]. Again, the pointers move one position further down the list, and the next iteration executes either case 3 or case 4. (c) Case 3: degree[x] = degree[next-x]
degree[next-x]. The pointers move one position further down the root list. (b) Case 2: degree[x] = degree[next-x] = degree[sibling[next-x]]. Again, the pointers move one position further down the list, and the next iteration executes either case 3 or case 4. (c) Case 3: degree[x] = degree[next-x]  degree[sibling[next-x] and key[x]
degree[sibling[next-x] and key[x]  key[next-x]. We remove next-x from the root list and link it to x, creating a Bk+1-tree. (d) Case 4: degree[x] = degree[next-x]
key[next-x]. We remove next-x from the root list and link it to x, creating a Bk+1-tree. (d) Case 4: degree[x] = degree[next-x]  degree[sibling[next-x]] and key[next-x]
degree[sibling[next-x]] and key[next-x]  key[x]. We remove x from the root list and link it to next-x, again creating a B k+1-tree.
key[x]. We remove x from the root list and link it to next-x, again creating a B k+1-tree.Inserting a node
BINOMIAL-HEAP-INSERT(H,x)
1 H'
 MAKE-BINOMIAL-HEAP()
MAKE-BINOMIAL-HEAP()2 p[x]
 NIL
NIL3 child[x]
 NIL
NIL4 sibling[x]
 NIL
NIL5 degree[x]
 0
06 head[H']
 x
x7 H
 BINOMIAL-HEAP-UNION(H,H')
BINOMIAL-HEAP-UNION(H,H')Extracting the node with minimum key
BINOMIAL-HEAP-EXTRACT-MIN(H)
1 find the root x with the minimum key in the root list of H,
and remove x from the root list of H
2 H'
 MAKE-BINOMIAL-HEAP()
MAKE-BINOMIAL-HEAP()3 reverse the order of the linked list of x's children,
and set head[H'] to point to the head of the resulting list
4 H
 BINOMIAL-HEAP-UNION(H,H')
BINOMIAL-HEAP-UNION(H,H')5 return x

Figure 20.7 The action of BINOMIAL-HEAP-EXTRACT-MIN. (a) A binomial heap H. (b) The root x with minimum key is removed from the root list of H. (c) The linked list of x's children is reversed, giving another binomial heap H'. (d) The result of uniting H and H'.
Decreasing a key
BINOMIAL-HEAP-DECREASE-KEY (H,x,k)
1 if k > key[x]
2 then error "new key is greater than current key"
3 key[x]
 k
k4 y
 x
x5 z
 p[y]
p[y]6 while z
 NIL and key[y] < key[z]
NIL and key[y] < key[z]7 do exchange key[y]
 key[z]
key[z]8
 If y and z have satellite fields, exchange them, too.
If y and z have satellite fields, exchange them, too.9 y
 z
z10 z
 p[y]
p[y] key[z], the binomial tree is now heap-ordered. Otherwise, node y violates heap ordering, so its key is exchanged with the key of its parent z, along with any other satellite information. The procedure then sets y to z, going up one level in the tree, and continues with the next iteration.
key[z], the binomial tree is now heap-ordered. Otherwise, node y violates heap ordering, so its key is exchanged with the key of its parent z, along with any other satellite information. The procedure then sets y to z, going up one level in the tree, and continues with the next iteration. lg n
lg n , so the while loop of lines 6-10 iterates at most
, so the while loop of lines 6-10 iterates at most  lg n
lg n times.
times.Deleting a key
 .
.
Figure 20.8 The action of BINOMIAL-HEAP-DECREASE-KEY. (a) The situation just before line 5 of the first iteration of the while loop. Node y has had its key decreased to 7, which is less than the key of y's parent z. (b) The keys of the two nodes are exchanged, and the situation just before line 5 of the second iteration is shown. Pointers y and z have moved up one level in the tree, but heap order is still violated. (c) After another exchange and moving pointers y and z up one more level, we finally find that heap order is satisfied, so the while loop terminates.
BINOMIAL-HEAP-DELETE(H,x)
1 BINOMIAL-HEAP-DECREASE-KEY(H,x,-
 )
)2 BINOMIAL-HEAP-EXTRACT-MIN(H)
 . (Exercise 20.2-6 deals with the situation in which -
. (Exercise 20.2-6 deals with the situation in which - cannot appear as a key, even temporarily.) It then bubbles this key and the associated satellite information up to a root by calling BINOMIAL-HEAP-DECREASE-KEY. This root is then removed from H by a call of BINOMIAL-HEAP-EXTRACT-MIN.
cannot appear as a key, even temporarily.) It then bubbles this key and the associated satellite information up to a root by calling BINOMIAL-HEAP-DECREASE-KEY. This root is then removed from H by a call of BINOMIAL-HEAP-EXTRACT-MIN.Exercises
 (n) time on the concatenation of their arrays.
(n) time on the concatenation of their arrays. . Rewrite the pseudocode to make it work correctly in such cases.
. Rewrite the pseudocode to make it work correctly in such cases. . Rewrite the BINOMIAL-HEAP-DELETE procedure to work correctly in this situation. It should still take O(lg n) time.
. Rewrite the BINOMIAL-HEAP-DELETE procedure to work correctly in this situation. It should still take O(lg n) time. (lg n) time. Explain why the worst-case running times of BINOMIAL-HEAP-INSERT, BINOMIAL-HEAP-MINIMUM, and BINOMIAL-HEAP-UNION are
(lg n) time. Explain why the worst-case running times of BINOMIAL-HEAP-INSERT, BINOMIAL-HEAP-MINIMUM, and BINOMIAL-HEAP-UNION are  (lg n) but not
(lg n) but not  (lg n). (See Problem 2-5.)
(lg n). (See Problem 2-5.)Problems
 key[x].
key[x]. R. We call w(u,v) the weight of edge (u, v). We wish to find a minimum spanning tree for G: an acyclic subset T
R. We call w(u,v) the weight of edge (u, v). We wish to find a minimum spanning tree for G: an acyclic subset T  E that connects all the vertices in V and whose total weight
E that connects all the vertices in V and whose total weight
Ei
 {(u,v): u
{(u,v): u  Vi or v
Vi or v  Vi}
Vi}
Chapter notes


