From a theoretical standpoint, Fibonacci heaps are especially desirable when the number of EXTRACT-MIN and DELETE operations is small relative to the number of other operations performed. This situation arises in many applications. For example, some algorithms for graph problems may call DECREASE-KEY once per edge. For dense graphs, which have many edges, the O(1) amortized time of each call of DECREASE-KEY adds up to a big improvement over the (lg n) worst-case time of binary or binomial heaps. The asymptotically fastest algorithms to date for problems such as computing minimum spanning trees (Chapter 24) and finding single-source shortest paths (Chapter 25) make essential use of Fibonacci heaps.
(lg n) worst-case time of binary or binomial heaps. The asymptotically fastest algorithms to date for problems such as computing minimum spanning trees (Chapter 24) and finding single-source shortest paths (Chapter 25) make essential use of Fibonacci heaps.
From a practical point of view, however, the constant factors and programming complexity of Fibonacci heaps make them less desirable than ordinary binary (or k-ary) heaps for most applications. Thus, Fibonacci heaps are predominantly of theoretical interest. If a much simpler data structure with the same amortized time bounds as Fibonacci heaps were developed, it would be of great practical use as well.
Like a binomial heap, a Fibonacci heap is a collection of trees. Fibonacci heaps, in fact, are loosely based on binomial heaps. If neither DECREASE-KEY nor DELETE is ever invoked on a Fibonacci heap, each tree in the heap is like a binomial tree. Fibonacci heaps differ from binomial heaps, however, in that they have a more relaxed structure, allowing for improved asymptotic time bounds. Work that maintains the structure can be delayed until it is convenient to perform.
Like the dynamic tables of Section 18.4, Fibonacci heaps offer a good example of a data structure designed with amortized analysis in mind. The intuition and analyses of Fibonacci heap operations in the remainder of this chapter rely heavily on the potential method of Section 18.3.
The exposition in this chapter assumes that you have read Chapter 20 on binomial heaps. The specifications for the operations appear in that chapter, as does the table in Figure 20.1, which summarizes the time bounds for operations on binary heaps, binomial heaps, and Fibonacci heaps. Our presentation of the structure of Fibonacci heaps relies on that of binomial heap structure. You will also find that some of the operations performed on Fibonacci heaps are similar to those performed on binomial heaps.
Like binomial heaps, Fibonacci heaps are not designed to give efficient support to the operation SEARCH; operations that refer to a given node therefore require a pointer to that node as part of their input.
Section 21.1 defines Fibonacci heaps, discusses their representation, and presents the potential function used for their amortized analysis. Section 21.2 shows how to implement the mergeable-heap operations and achieve the amortized time bounds shown in Figure 20.1. The remaining two operations, DECREASE-KEY and DELETE, are presented in Section 21.3. Finally, Section 21.4 finishes off a key part of the analysis.
21.1 Structure of Fibonacci heaps
Like a binomial heap, a Fibonacci heap is a collection of heap-ordered trees. The trees in a Fibonacci heap are not constrained to be binomial trees, however. Figure 21.1 (a) shows an example of a Fibonacci heap.
Unlike trees within binomial heaps, which are ordered, trees within Fibonacci heaps are rooted but unordered. As Figure 21.1(b) shows, each node x contains a pointer p[x] to its parent and a pointer child[x] to any one of its children. The children of x are linked together in a circular, doubly linked list , which we call the child list of x. Each child y in a child list has pointers left[y] and right[y] that point to y's left and right siblings, respectively. If node y is an only child, then left[y] = right[y] = y. The order in which siblings appear in a child list is arbitrary.
Circular, doubly linked lists (see Section 11.2) have two advantages for use in Fibonacci heaps. First, we can remove a node from a circular, doubly linked list in O(1) time. Second, given two such lists, we can concatenate them (or "splice" them together) into one circular, doubly linked list in O(1) time. In the descriptions of Fibonacci heap operations, we shall refer to these operations informally, letting the reader fill in the details of their implementations.
Two other fields in each node will be of use. The number of children in the child list of node x is stored in degree[x]. The boolean-valued field mark[x] indicates whether node x has lost a child since the last time x was made the child of another node. We won't worry about the details of marking nodes until Section 21.3. Newly created nodes are unmarked, and a node x becomes unmarked whenever it is made the child of another node.
A given Fibonacci heap H is accessed by a pointer min[H] to the root of the tree containing a minimum key; this node is called the minimum node of the Fibonacci heap. If a Fibonacci heap H his empty, then min[H] = NIL.
The roots of all the trees in a Fibonacci heap are linked together using their left and right pointers into a circular, doubly linked list called the root list of the Fibonacci heap. The pointer min[H] thus points to the node in the root list whose key is minimum. The order of the trees within a root list is arbitrary.
We rely on one other attribute for a Fibonacci heap H: the number of nodes currently in H is kept in n[H].
As mentioned, we shall use the potential method of Section 18.3 to analyze the performance of Fibonacci heap operations. For a given Fibonacci heap H, we indicate by t(H) the number of trees in the root list of H and by m (H) the number of marked nodes in H. The potential of Fibonacci heap H is then defined by
For example, the potential of the Fibonacci heap shown in Figure 21.1 is 5 + 2
We assume that a Fibonacci heap application begins with no heaps. The initial potential, therefore, is 0, and by equation (21.1), the potential is nonnegative at all subsequent times. From equation (18.2), an upper bound on the total amortized cost is thus an upper bound on the total actual cost for the sequence of operations.
The amortized analyses we shall perform in the remaining sections of this chapter assume that there is a known upper bound D(n) on the maximum degree of any code in an n-node Fibonacci heap. Exercise 21.2-3 shows that when only the mergeable-heap operations are supported, D(n) =
In this section, we describe and analyze the mergeable-heap operations as implemented for Fibonacci heaps. If only these operations--MAKE-HEAP, INSERT, MINIMUM, EXTRACT-MIN, and UNION--are to be supported, each Fibonacci heap is simply a collection of "unordered" binomial trees. An unordered binomial tree is like a binomial tree, and it, too, is defined recursively. The unordered binomial tree U0 consists of a single node, and an unordered binomial tree Uk consists of two unordered binomial trees Uk-1 for which the root of one is made into any child of the root of the other. Lemma 20.1, which gives properties of binomial trees, holds for unordered binomial trees as well, but with the following variation on property 4 (see Exercise 21.2-2):
4' For the unordered binomial tree Uk.The root has degree k, which is greater than that of any other node. The children of the root are roots of subtrees U0, U1, . . . , Uk-1 in some order.
Thus, if an n-node Fibonacci in heap is a collection of unordered binomial trees, then D(n) = lg n.
The key idea in the mergeable-heap operations on Fibonacci heaps is to delay work as long as possible. There is a performance trade-off among implementations of the various operations. If the number of trees in a Fibonacci heap is small, then we can quickly determine the new minimum node during an EXTRACT-MIN operation. However, as we saw with binomial heaps in Exercise 20.2-10, we pay a price for ensuring that the number of trees is small: it can take up to
To make an empty Fibonacci heap, the MAKE-FIB-HEAP procedure allocates and returns the Fibonacci heap object H, where n[H] = 0 and min[H] = NIL; there are no trees in H. Because t (H) = 0 and m(H) = 0, the potential of the empty Fibonacci heap is
The following procedure inserts node x into Fibonacci heap H, assuming of course that the node has already been allocated and that key[x] has already been filled in.
After lines 1-6 initialize the structural fields of node x, making it its own circular, doubly linked list , line 7 adds x to the root list of H in O(1) actual time. Thus, node x becomes a single-node heap-ordered tree, and thus an unordered binomial tree, in the Fibonacci heap. It has no children and is unmarked. Lines 8-9 then update the pointer to the minimum node of Fibonacci heap H if necessary. Finally, line 10 increments n[H] to reflect the addition of the new node. Figure 21.2 shows a node with key 21 inserted into the Fibonacci heap of Figure 21.1.
Unlike the BINOMIAL-HEAP-INSERT procedure, FIB-HEAP-INSERT makes no attempt to consolidate the trees within the Fibonacci heap. If k consecutive FIB-HEAP-INSERT operations occur, then k single-node trees are added to the root list.
To determine the amortized cost of FIB-HEAP-INSERT, let H be the input Fibonacci heap and H' be the resulting Fibonacci heap. Then, t(H') = t(H) + 1 and m(H') = m(H), and the increase in potential is
Since the actual cost is O(1), the amortized cost is O(1) + 1 = O(1).
The minimum node of a Fibonacci heap H is given by the pointer min[H], so we can find the minimum node in O(1) actual time. Because the potential of H does not change, the amortized cost of this operation is equal to its O(1) actual cost.
The following procedure unites Fibonacci heaps H1 and H2, destroying H1 and H2 in the process.
Lines 1-3 concatenate the root lists of H1 and H2 into a new root list H. Lines 2, 4, and 5 set the minimum node of H, and line 6 sets n[H] to the total number of nodes. The Fibonacci heap objects H1 and H2 are freed in line 7, and line 8 returns the resulting Fibonacci heap H. As in the FIB-HEAP-INSERT procedure, no consolidation of trees occurs.
The change in potential is
because t(H) = t(H1) + t(H2) and m(H) = m(H1) + m(H2). The amortized cost of FIB-HEAP-UNION is therefore equal to its O(1) actual cost.
The process of extracting the minimum node is the most complicated of the operations presented in this section. It is also where the delayed work of consolidating trees in the root list finally occurs. The following pseudocode extracts the minimum node. The code assumes for convenience that when a node is removed from a linked list, pointers remaining in the list are updated, but pointers in the extracted node are left unchanged. It also uses the auxiliary procedure CONSOLIDATE, which will be presented shortly.
As shown in Figure 21.3, FIB-HEAP-EXTRACT-MIN works by first making a root out of each of the minimum node's children and removing the minimum node from the root list. It then consolidates the root list by linking roots of equal degree until at most one root remains of each degree.
We start in line 1 by saving a pointer z to the minimum node; this pointer is returned at the end. If z = NIL, then Fibonacci heap H is already empty and we are done. Otherwise, as in the BINOMIAL-HEAP-EXTRACT-MIN procedure, we delete node z from H by making all of z's children roots of H in lines 3-5 (putting them into the root list) and removing z from the root list in line 6. If z = right[z] after line 6, then z was the only node on the root list and it had no children, so all that remains is to make the Fibonacci heap empty in line 8 before returning z. Otherwise, we set the pointer min[H] into the root list to point to a node other than z (in this case, right[z]). Figure 21.3(b) shows the Fibonacci heap of Figure 21.3(a) after line 9 has been performed.
The next step, in which we reduce the number of trees in the Fibonacci heap, is consolidating the root list of H; this is performed by the call CONSOLIDATE(H). Consolidating the root list consists of repeatedly executing the following steps until every root in the root list has a distinct degree value.
1. Find two roots x and y in the root list with the same degree, where key[x]
2. Link y to x: remove y from the root list, and make y a child of x. This operation is performed by the FIB-HEAP-LINK procedure. The field degree[x] is incremented, and the mark on y, if any, is cleared.
The procedure CONSOLIDATE uses an auxiliary array A[0 . . D(n[H])]; if A[i] = y, then y is currently a root with degree[y] = i.
In detail, the CONSOLIDATE procedure works as follows. In lines 1-2, we initialize A by making each entry NIL. When we are done processing each root w, it ends up in a tree rooted at some node x, which may or may not be identical to w. Array entry A[degree[x]] will then be set to point to x. In the for loop of lines 3-13, we examine each root w in the root list. The invariant maintained during each iteration of the for loop is that node x is the root of the tree containing node w. The while loop of lines 6-12 maintains the invariant that d = degree[x] (except in line 11, as we shall see in a moment). In each iteration of the while loop, A[d] points to some root y. Because d = degree[x] = degree[y], we want to link x and y. Whichever of x and y has the smaller key becomes the parent of the other as a result of the link operation, and so lines 8-9 exchange the pointers to x and y if necessary. Next, we link y to x by the call FIB-HEAP-LINK(H,y,x) in line 10. This call increments degree[x] but leaves degree[y] as d. Because node y is no longer a root, the pointer to it in array A is removed in line 11. Because the value of degree[x] is incremented by the call of FIB-HEAP-LINK, line 12 restores the invariant that d = degree[x]. We repeat the while loop until A[d] = NIL, in which case there is no other root with the same degree as x. We set A[d] to x in line 13 and perform the next iteration of the for loop. Figures 21.3(c)-(e) show the array A and the resulting trees after the first three iterations of the for loop of lines 3-13. In the next iteration of the for loop, three links occur; their results are shown in Figures 21.3(f)-(h). Figures 21.3(i)-(1) show the result of the next four iterations of the for loop.
All that remains is to clean up. Once the for loop of lines 3-13 completes, line 14 empties the root list, and lines 15-19 reconstruct it. The resulting Fibonacci heap is shown in Figure 21.3(m). After consolidating the root list, FIB-HEAP-EXTRACT-MIN finishes up by decrementing n[H] in line 11 and returning a pointer to the deleted node z in line 12.
Observe that if all trees in the Fibonacci heap are unordered binomial trees before FIB-HEAP-EXTRACT-MIN is executed, then they are all unordered binomial trees afterward. There are two ways in which trees are changed. First, in lines 3-5 of FIB-HEAP-EXTRACT-MIN, each child x of root z becomes a root. By Exercise 21.2-2, each new tree is itself an unordered binomial tree. Second, trees are linked by FIB-HEAP-LINK only if they have the same degree. Since all trees are unordered binomial trees before the link occurs, two trees whose roots each have k children must have the structure of Uk. The resulting tree therefore has the structure of Uk+1.
We are now ready to show that the amortized cost of extracting the minimum node of an n-node Fibonacci heap is O(D(n)). Let H denote the Fibonacci heap just prior to the FIB-HEAP-EXTRACT-MIN operation.
The actual cost of extracting the minimum node can be accounted for as follows. An O(D(n)) contribution comes from there being at most D(n) children of the minimum node that are processed in FIB-HEAP-EXTRACT-MIN and from the work in lines 1-2 and 14-19 of CONSOLIDATE. It remains to analyze the contribution from the for loop of lines 3-13. The size of the root list upon calling CONSOLIDATE is at most D(n) + t(H) - 1, since it consists of the original t(H) root-list nodes, minus the extracted root node, plus the children of the extracted node, which number at most D(n). Every time through the while loop of lines 6-12, one of the roots is linked to another, and thus the total amount of work performed in the for loop is at most proportional to D(n) + t(H). Thus, the total actual work is O(D(n) + t(H)).
The potential before extracting the minimum node is t(H) + 2m(H), and the potential afterward is at most (D(n) + 1) + 2m(H), since at most D(n) + 1 roots remain and no nodes become marked during the operation. The amortized cost is thus at most
since we can scale up the units of potential to dominate the constant hidden in O(t(H)). Intuitively, the cost of performing each link is paid for by the reduction in potential due to the link reducing the number of roots by one.
21.2-1
Show the Fibonacci heap that results from calling FIB-HEAP-EXTRACT-MIN on the Fibonacci heap shown in Figure 21.3(m).
21.2-2
Prove that Lemma 20.1 holds for unordered binomial trees, but with property 4' in place of property 4.
21.2-3
Show that if only the mergeable-heap operations are supported, the maximum degree D(n) in an n-node Fibonacci heap is at most
21.2-4
Professor McGee has devised a new data structure based on Fibonacci heaps. A McGee heap has the same structure as a Fibonacci heap and supports the mergeable-heap operations. The implementations of the operations are the same as for Fibonacci heaps, except that insertion and union perform consolidation as their last step. What are the worst-case running time of operations on McGee heaps? How novel is the professor's data structure?
21.2-5
Argue that when the only operations on keys are comparing two keys (as is the case for all the implementations in this chapter), not all of the mergeable-heap operations can run in O(1) amortized time.
In this section, we show how to decrease the key of a node in a Fibonacci heap in O(1) amortized time and how to delete any node from an n-node Fibonacci heap in O(D(n)) amortized time. These operations do not preserve the property that all trees in the Fibonacci heap are unordered binomial trees. They are close enough, however, that we can bound the maximum degree D(n) by O(1g n). Proving this bound will imply that FIB-HEAP-EXTRACT-MIN and FIB-HEAP-DELETE run in O(1g n) amortized time.
In the following pseudocode for the operation FIB-HEAP-DECREASE-KEY, we assume as before that removing a node from a linked list does not change any of the structural fields in the removed node.
The FIB-HEAP-DECREASE-KEY procedure works as follows. Lines 1-3 ensure that the new key is no greater than the current key of x and then assign the new key to x. If x is a root or if key[x]
If heap order has been violated, many changes may occur. We start by cutting x in line 6. The CUT procedure "cuts" the link between x and its parent y, making x a root.
We use the mark fields to obtain the desired time bounds. They help to produce the following effect. Suppose that x is a node that has undergone the following history:
1. at some time, x was a root,
2. then x was linked to another node,
3. then two children of x were removed by cuts.
As soon as the second child has been lost, x is cut from its parent, making it a new root. The field mark[x] is TRUE if steps 1 and 2 have occurred and one child of x has been cut. The CUT procedure, therefore, clears mark[x] in line 4, since it performs step 1. (We can now see why line 3 of FIB-HEAP-LINK clears mark[y]: node y is being linked to another node, and so step 2 is being performed. The next time a child of y is cut, mark[y] will be set to TRUE.)
We are not yet done, because x might be the second child cut from its parent y since the time that y was linked to another node. Therefore, line 7 of FIB-HEAP-DECREASE-KEY performs a cascading-cut operation on y. If y is a root, then the test in line 2 of CASCADING-CUT causes the procedure to just return. If y is unmarked, the procedure marks it in line 4, since its first child has just been cut, and returns. If y is marked, however, it has just lost its second child; y is cut in line 5, and CASCADING-CUT calls itself recursively in line 6 on y's parent z. The CASCADING-CUT procedure recurses its way up the tree until either a root or an unmarked node is found.
Once all the cascading cuts have occurred, lines 8-9 of FIB-HEAP-DECREASE-KEY finish up by updating min[H] if necessary.
Figure 21.4 shows the execution of two calls of FIB-HEAP-DECREASE-KEY, starting with the Fibonacci heap shown in Figure 21.4(a). The first call, shown in Figure 21.4(b), involves no cascading cuts. The second call, shown in Figures 21.4(c)-(e), invokes two cascading cuts.
We shall now show that the amortized cost of FIB-HEAP-DECREASE-KEY is only O(1). We start by determining its actual cost. The FIB-HEAP-DECREASE-KEY procedure takes O(1) time, plus the time to perform the cascading cuts. Suppose that CASCADING-CUT is recursively called c times from a given invocation of FIB-HEAP-DECREASE-KEY. Each call of CASCADING-CUT takes O(1) time exclusive of recursive calls. Thus, the actual cost of FIB-HEAP-DECREASE-KEY, including all recursive calls, is O(c).
We next compute the change in potential. Let H denote the Fibonacci heap just prior to the FIB-HEAP-DECREASE-KEY operation. Each recursive call of CASCADING-CUT, except for the last one, cuts a marked node and clears the mark bit. Afterward, there are t(H) + c trees (the original t(H) trees, c- 1 trees produced by cascading cuts, and the tree rooted at x) and at most m(H) - c + 2 marked nodes (c - 1 were unmarked by cascading cuts and the last call of CASCADING-CUT may have marked a node). The change in potential is therefore at most
Thus, the amortized cost of FIB-HEAP-DECREASE-KEY is at most
since we can scale up the units of potential to dominate the constant hidden in O(c).
You can now see why the potential function was defined to include a term that is twice the number of marked nodes. When a marked node y is cut by a cascading cut, its mark bit is cleared, so the potential is reduced by 2. One unit of potential pays for the cut and the clearing of the mark bit, and the other unit compensates for the unit increase in potential due to node y becoming a root.
It is easy to delete a node from an n-node Fibonacci heap in O(D(n)) amortized time, as is done by the following pseudocode. We assume that there is no key value of -
FIB-HEAP-DELETE is analogous to BINOMIAL-HEAP-DELETE. It makes x become the minimum node in the Fibonacci heap by giving it a uniquely small key of -
21.3-1
Suppose that a root x in a Fibonacci heap is marked. Explain how x came to be a marked root. Argue that it doesn't matter to the analysis that x is marked, even though it is not a root that was first linked to another node and then lost one child.
21.3-2
Justify the O(1) amortized time of FIB-HEAP-DECREASE-KEY using the aggregate method of Section 18.1.
To prove that the amortized time of FIB-HEAP-EXTRACT-MIN and FIB-HEAP-DELETE is O(lg n), we must show that the upper bound D(n) on the degree of any node of an n-node Fibonacci heap is O(lg n). By Exercise 21.2-3, when all trees in the Fibonacci heap are unordered binomial trees, D(n) =
The key to the analysis is as follows. For each node x within a Fibonacci heap, define size(x) to be the number of nodes, including x itself, in the subtree rooted at x. (Note that x need not be in the root list--it can be any node at all.) We shall show that size(x) is exponential in degree[x]. Bear in mind that degree[x] is always maintained as an accurate count of the degree of x.
Lemma 21.1
Let x be any node in a Fibonacci heap, and suppose that degree[x] = k. Let y1, y2, ..., yk denote the children of x in the order in which they were linked to x, from the earliest to the latest. Then, degree [y1]
Proof Obviously, degree[y1]
For i
We finally come to the part of the analysis that explains the name "Fibonacci heaps." Recall from Section 2.2 that for k = 0, 1, 2, . . . , the kth Fibonacci number is defined by the recurrence
The following lemma gives another way to express Fk.
Lemma 21.2
For all integers k
Proof The proof is by induction on k. When k = 0,
We now assume the inductive hypothesis that
The following lemma and its corollary complete the analysis. It uses the inequality (proved in Exercise 2.2-8)
where
Lemma 21.3
Let x be any node in a Fibonacci heap, and let k = degree[x]. Then, size (x)
Proof Let sk denote the minimum possible value of size(z) over all nodes z such that degree[z] = k. Trivially, s0 = 1, s1 = 2, and s2 = 3. The number sk is at most size(x). As in Lemma 21.1, let y1, y2, . . . , yk denote the children of x in the order in which they were linked to x. To compute a lower bound on size(x), we count one for x itself and one for the first child y1 (for which size(y1)
We now show by induction on k that sk
The last equality follows from Lemma 21.2.
Thus, we have shown that size(x)
Corollary 21.4
The maximum degree D(n) of any node in an n-node Fibonacci heap is O(lg n).
Proof Let x be any node in an n-node Fibonacci heap, and let k = degree[x]. By Lemma 21.3, we have n
21.4-1
Professor Pinocchio claims that the height of an n-node Fibonacci heap is O(lg n). Show that the professor is mistaken by exhibiting, for any positive integer n, a sequence of Fibonacci-heap operations that creates a Fibonacci heap consisting of just one tree that is a linear chain of n nodes.
21.4-2
Suppose we generalize the cascading-cut rule to cut a node x from its parent as soon as it loses its kth child, for some integer constant k. (The rule in Section 21.3 uses k = 2.) For what values of k is D(n) = O(lg n)?
21-1 Alternative implementation of deletion
Professor Pisano has proposed the following variant of the FIB-HEAP-DELETE procedure, claiming that it runs faster when the node being deleted is not the node pointed to by min[H].
a. The professor's claim that this procedure runs faster is based partly on the assumption that line 7 can be performed in O(1) actual time. What is wrong with this assumption?
b. Give a good upper bound on the actual time of PISANO-DELETE when x
c. Let H' be the Fibonacci heap that results from an execution of PISANO-DELETE(H, x). Assuming that node x is not a root, bound the potential of H' in terms of degree[x], c, t(H), and m(H).
d. Conclude that the amortized time for PISANO-DELETE is asymptotically no better than for FIB-HEAP-DELETE, even when x
21-2 More Fibonacci-heap operations
We wish to augment a Fibonacci heap H to support two new operations without changing the amortized running time of any other Fibonacci-heap operations.
a. Give an efficient implementation of the operation FIB-HEAP-CHANGE-KEY(H, x, k), which changes the key of node x to the value k. Analyze the amortized running time of your implementation for the cases in which k is greater than, less than, or equal to key[x].
b. Give an efficient implementation of FIB-HEAP-PRUNE(H, r), which deletes min(r, n[H]) nodes from H. Which nodes are deleted should be arbitrary. Analyze the amortized running time of your implementation. (Hint: You may need to modify the data structure and potential function.)
Fibonacci heaps were introduced by Fredman and Tarjan [75]. Their paper also describes the application of Fibonacci heaps to the problems of single-source shortest paths, all-pairs shortest pairs, weighted bipartite matching, and the minimum-spanning-tree problem.
Subsequently, Driscoll, Sarnak, Sleator, and Tarjan [58] developed "relaxed heaps" as an alternative to Fibonacci heaps. There are two varieties of relaxed heaps. One gives the same amortized time bounds as Fibonacci heaps. The other allows DECREASE-KEY to run in O(1) worst-case (not amortized) time and EXTRACT-MIN and DELETE to run in O(lg n) worst-case time. Relaxed heaps also have some advantages over Fibonacci heaps in parallel algorithms.
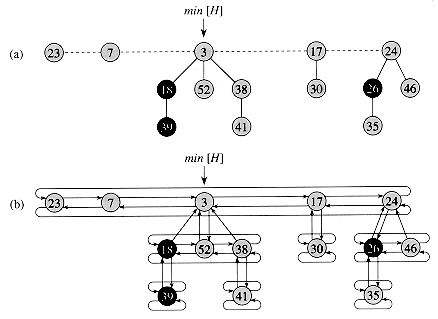
Figure 21.1 (a) A Fibonacci heap consisting of five heap-ordered trees and 14 nodes. The dashed line indicates the root list. The minimum node of the heap is the node containing the key 3. The three marked nodes are blackened. The potential of this particular Fibonacci heap is 5 + 2
 3 = 11. (b) A more complete representation showing pointers p (up arrows), child (down arrows), and left and right (sideways arrows). These details are omitted in the remaining figures in this chapter, since all the information shown here can be determined from what appears in part (a).
3 = 11. (b) A more complete representation showing pointers p (up arrows), child (down arrows), and left and right (sideways arrows). These details are omitted in the remaining figures in this chapter, since all the information shown here can be determined from what appears in part (a).Potential function
 (H) = t(H) + 2m(H) .
(H) = t(H) + 2m(H) .(21.1)
 3 = 11. The potential of a set of Fibonacci heaps is the sum of the potentials of its constituent Fibonacci heaps. We shall assume that a unit of potential can pay for a constant amount of work, where the constant is sufficiently large to cover the cost of any of the specific constant-time pieces of work that we might encounter.
3 = 11. The potential of a set of Fibonacci heaps is the sum of the potentials of its constituent Fibonacci heaps. We shall assume that a unit of potential can pay for a constant amount of work, where the constant is sufficiently large to cover the cost of any of the specific constant-time pieces of work that we might encounter.Maximum degree
 lg n
lg n . In Section 21.3, we shall show that when we support DECREASE-KEY and DELETE as well, D(n) = O(lg n).
. In Section 21.3, we shall show that when we support DECREASE-KEY and DELETE as well, D(n) = O(lg n).21.2 Mergeable-heap operations
 (1g n) time to insert a node into a binomial heap or to unite two binomial heaps. As we shall see, we do not attempt to consolidate trees in a Fibonacci heap when we insert a new node or unite two heaps. We save the consolidation for the EXTRACT-MIN operation, which is when we really need to find the new minimum node.
(1g n) time to insert a node into a binomial heap or to unite two binomial heaps. As we shall see, we do not attempt to consolidate trees in a Fibonacci heap when we insert a new node or unite two heaps. We save the consolidation for the EXTRACT-MIN operation, which is when we really need to find the new minimum node.Creating a new Fibonacci heap
 (H) = 0. The amortized cost of MAKE-FIB-HEAP is thus equal to its O(1) actual cost.
(H) = 0. The amortized cost of MAKE-FIB-HEAP is thus equal to its O(1) actual cost.Inserting a node
FIB-HEAP-INSERT(H, x)
1 degree[x]
 0
02 p[x]
 NIL
NIL3 child[x]
 NIL
NIL4 left[x]
 x
x5 right[x]
 x
x6 mark[x]
 FALSE
FALSE7 concatenate the root list containing x with root list H
8 if min[H] = NIL or key[x] < key[min[H]]
9 then min[H]
 x
x10 n[H]
 n[H] + 1
n[H] + 1
Figure 21.2 Inserting a node into a Fibonacci heap. (a) A Fibonacci heap H. (b) Fibonacci heap H after the node with key 21 has been inserted. The node becomes its own heap-ordered tree and is then added to the root list, becoming the left sibling of the root.
((t(H) + 1) + 2m(H)) - (t(H) + 2m(H)) = 1 .
Finding the minimum node
Uniting two Fibonacci heaps
FIB-HEAP-UNION(H1,H2)
1 H
 MAKE-FIB-HEAP()
MAKE-FIB-HEAP()2 min[H]
 min[H1]
min[H1]3 concatenate the root list of H2 with the root list of H
4 if (min[H1] = NIL) or (min[H2]
 NIL and min[H2] < min[H1])
NIL and min[H2] < min[H1])5 then min[H]
 min[H2]
min[H2]6 n[H]
 n[H1] + n[H2]
n[H1] + n[H2]7 free the objects H1 and H2
8 return H
 (H) - (
(H) - ( (H1) +
(H1) +  (H2))
(H2))= (t(H) + 2m(H)) - ((t(H1) + 2 m(H1)) + (t(H2) + 2m(H2)))
= 0,
Extracting the minimum node
FIB-HEAP-EXTRACT-MIN(H)
1 z
 min[H]
min[H]2 if z
 NIL
NIL3 then for each child x of z
4 do add x to the root list of H
5 p[x]
 NIL
NIL6 remove z from the root list of H
7 if z = right[z]
8 then min[H]
 NIL
NIL9 else min[H]
 right[z]
right[z]10 CONSOLIDATE(H)
11 n[H]
 n[H] - 1
n[H] - 112 return z
 key[y].
key[y].CONSOLIDATE(H)
1 for i
 0 to D(n[H])
0 to D(n[H])2 do A[i]
 NIL
NIL3 for each node w in the root list of H
4 do x
 w
w5 d
 degree[x]
degree[x]6 while A[d]
 NIL
NIL7 do y
 A[d]
A[d]8 if key[x] > key[y]
9 then exchange x
 y
y10 FIB-HEAP-LINK(H,y,x)
11 A[d]
 NIL
NIL12 d
 d + 1
d + 113 A[d]
 x
x14 min[H]
 NIL
NIL15 for i
 0 to D(n[H])
0 to D(n[H])16 do if A[i]
 NIL
NIL17 then add A[i] to the root list of H
18 if min[H] = NIL or key[A[i]] < key[min[H]]
19 then min[H]
 A[i]
A[i]FIB-HEAP-LINK(H, y, x)
1 remove y from the root list of H
2 make y a child of x, incrementing degree[x]
3 mark[y]
 FALSE
FALSE
Figure 21.3 The action of FIB-HEAP-EXTRACT-MIN. (a) A Fibonacci heap H. (b) The situation after the minimum node z is removed from the root list and its children are added to the root list. (c)-(e) The array A and the trees after each of the first three iterations of the for loop of lines 3-13 of the procedure CONSOLIDATE. The root list is processed by starting at the minimum node and following right pointers. Each part shows the values of w and x at the end of an iteration. (f)-(h) The next iteration of the for loop, with the values of w and x shown at the end of each iteration of the while loop of lines 6-12. Part (f) shows the situation after the first time through the while loop. The node with key 23 has been linked to the node with key 7, which is now pointed to by x. In part (g), the node with key 17 has been linked to the node with key 7, which is still pointed to by x. In part (h), the node with key 24 has been linked to the node with key 7. Since no node was previously pointed to by A[3], at the end of the for loop iteration, A[3] is set to point to the root of the resulting tree. (i)-(l) The situation after each of the next four iterations of the while loop. (m) Fibonacci heap H after reconstruction of the root list from the array A and determination of the new min[H] pointer.

O(D(n) + t(H)) + ((D(n) + 1) + 2m(H)) - (t(H) + 2m(H))
= O(D(n)) + O(t(H)) - t(H)
= O(D(n)),
Exercises
 1g n
1g n .
.21.3 Decreasing a key and deleting a node
Decreasing a key
FIB-HEAP-DECREASE-KEY(H,x,k)
1 if k > key[x]
2 then error "new key is greater than current key"
3 key[x]
 k
k4 y
 p[x]
p[x]5 if y
 NIL and key[x] < key[y]
NIL and key[x] < key[y]6 then CUT(H,x,y)
7 CASCADING-CUT(H,y)
8 if key[x] < key[min[H]]
9 then min[H]
 x
xCUT(H,x,y)
1 remove x from the child list of y, decrementing degree[y]
2 add x to the root list of H
3 p[x]
 NIL
NIL4 mark[x]
 FALSE
FALSECASCADING-CUT(H,y)
1 z
 p[y]
p[y]2 if z
 NIL
NIL3 then if mark[y] = FALSE
4 then mark[y]
 TRUE
TRUE5 else CUT(H,y,z)
6 CASCADING-CUT(H,z)
 key[y], where y is x's parent, then no structural changes need occur, since heap order has not been violated. Lines 4-5 test for this condition.
key[y], where y is x's parent, then no structural changes need occur, since heap order has not been violated. Lines 4-5 test for this condition.((t(H) + c) + 2(m(H) - c + 2)) - (t(H) + 2m(H)) = 4 - c .
O(c) + 4 - c = O(1) ,

Figure 21.4 Two calls of FIB-HEAP-DECREASE-KEY. (a) The initial Fibonacci heap. (b) The node with key 46 has its key decreased to 15. The node becomes a root, and its parent (with key 24), which had previously been unmarked, becomes marked. (c)-(e) The node with key 35 has its key decreased to 5. In part (c), the node, now with key 5, becomes a root. Its parent, with key 26, is marked, so a cascading cut occurs. The node with key 26 is cut from its parent and made an unmarked root in (d). Another cascading cut occurs, since the node with key 24 is marked as well. This node is cut from its parent and made an unmarked root in part (e). The cascading cuts stop at this point, since the node with key 7 is a root. (Even if this node were not a root, the cascading cuts would stop, since it is unmarked.) The result of the FIB-HEAP-DECREASE-KEY operation is shown in part (e), with min[H] pointing to the new minimum node.
Deleting a node
 currently in the Fibonacci heap.
currently in the Fibonacci heap.FIB-HEAP-DELETE(H, x)
1 FIB-HEAP-DECREASE-KEY(H, x, -
 )
)2 FIB-HEAP-EXTRACT-MIN(H)
 . Node x is then removed from the Fibonacci heap by the FIB-HEAP-EXTRACT-MIN procedure. The amortized time of FIB-HEAP-DELETE is the sum of the O(1) amortized time of FIB-HEAP-DECREASE-KEY and the O(D(n)) amortized time of FIB-HEAP-EXTRACT-MIN.
. Node x is then removed from the Fibonacci heap by the FIB-HEAP-EXTRACT-MIN procedure. The amortized time of FIB-HEAP-DELETE is the sum of the O(1) amortized time of FIB-HEAP-DECREASE-KEY and the O(D(n)) amortized time of FIB-HEAP-EXTRACT-MIN.Exercises
21.4 Bounding the maximum degree
 lg n
lg n . The cuts that occur in FIB-HEAP-DECREASE-KEY, however, may cause trees within the Fibonacci heap to violate the unordered binomial tree properties. In this section, we shall show that because we cut a node from its parent as soon as it loses two children, D(n) is O(lg n). In particular, we shall show that D(n)
. The cuts that occur in FIB-HEAP-DECREASE-KEY, however, may cause trees within the Fibonacci heap to violate the unordered binomial tree properties. In this section, we shall show that because we cut a node from its parent as soon as it loses two children, D(n) is O(lg n). In particular, we shall show that D(n) 
 log
log n
n , where
, where  .
. 0 and degree[yi]
0 and degree[yi]  i - 2 for i = 2, 3, . . . , k.
i - 2 for i = 2, 3, . . . , k. 0.
0. 2, we note that when yi was linked to x, all of y1, y2, . . . , yi-1 were children of x, so we must have had degree[x]
2, we note that when yi was linked to x, all of y1, y2, . . . , yi-1 were children of x, so we must have had degree[x]  i - 1. Node yi is linked to x only if degree[x] = degree[yi], so we must have also had degree[yi]
i - 1. Node yi is linked to x only if degree[x] = degree[yi], so we must have also had degree[yi]  i - 1 at that time. Since then, node yi has lost at most one child, since it would have been cut from x if it had lost two children. We conclude that degree [yi ]
i - 1 at that time. Since then, node yi has lost at most one child, since it would have been cut from x if it had lost two children. We conclude that degree [yi ]  i - 2.
i - 2. 
 0,
0,

 , and we have
, and we have
Fk+2

 k ,
k , is the golden ratio defined in equation (2.14) as
is the golden ratio defined in equation (2.14) as  .
. Fk+2
Fk+2 
 k, where
k, where  =
=  .
. 1 ) and then apply Lemma 21.1 for the other children. We thus have
1 ) and then apply Lemma 21.1 for the other children. We thus have
 Fk+2 for all nonnegative integer k. The bases, for k = 0 and k = 1, are trivial. For the inductive step, we assume that k
Fk+2 for all nonnegative integer k. The bases, for k = 0 and k = 1, are trivial. For the inductive step, we assume that k  2 and that si
2 and that si  Fi + 2 for i = 0, 1, . . . , k - 1. We have
Fi + 2 for i = 0, 1, . . . , k - 1. We have
 sk + 2
sk + 2 
 k.
k.  size(x)
size(x) 
 k. Taking base-
k. Taking base- logarithms yields k
logarithms yields k  log
log n. (In fact, because k is an integer, k
n. (In fact, because k is an integer, k 
 log
log n
n .) The maximum degree D(n) of any node is thus O(lg n).
.) The maximum degree D(n) of any node is thus O(lg n). Exercises
Problems
PISANO-DELETE(H, x)
1 if x = min[H]
2 then FIB-HEAP-EXTRACT-MIN(H)
3 else y
 p[x]
p[x]4 if y
 NIL
NIL5 then CUT(H,x,y)
6 CASCADING-CUT(H,y)
7 add x's child list to the root list of H
8 remove x from the root list of H
 min[H]. Your bound should be in terms of degree[x] and the number c of calls to the CASCADING-CUT procedure.
min[H]. Your bound should be in terms of degree[x] and the number c of calls to the CASCADING-CUT procedure. min[H].
min[H].Chapter notes


