Advanced Hierarchical Spherical Parameterizations
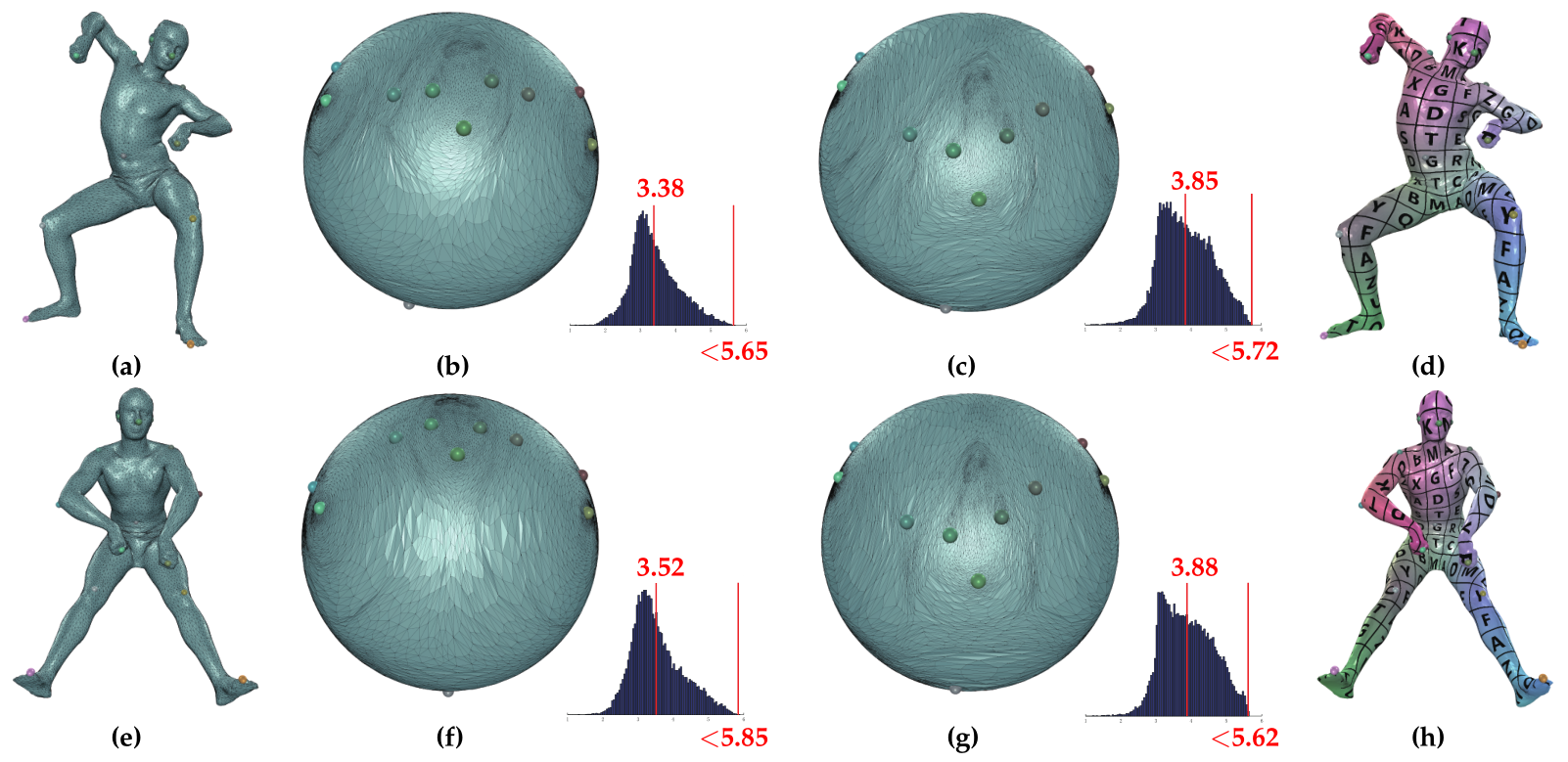
Figure 1: Examples of spherical parameterizations and surface correspondence.
Abstract
Computing spherical parameterizations for genus-zero closed surfaces is a fundamental task for geometric processing and computer graphics. Existing methods usually suffer from a lack of practical robustness or poor quality. In this paper, we present a practically robust method to compute high-quality spherical parameterizations with bijection and low isometric distortion. Our method is based on the hierarchical scheme containing mesh decimation and parameterization refinement. The practical robustness of our method relies on two novel techniques. The first one is a flat-to-extrusive decimation strategy, which contains two decimation error metrics to alleviate the difficulty for further mesh refinement. The second is a flexible group refinement technique that consists of flexible vertex insertion and efficient volumetric distortion minimization to control the maximum distortion. We convert the task of volumetric distortion minimization to the one of tetrahedral mesh improvement to make the vertices distribute uniformly for efficient refinement. Compared with state-of-the-art methods, our method is more practically robust and possesses better mapping qualities. We demonstrate the efficacy of our method in spherical parameterization computations on a data set containing over five thousand complex models.
Downloads
BaiduYun: Paper, Paper(Low), Data set, Code, Video.
Dropbox: Paper, Paper(Low), Data set, Code, Video.
5181 meshes (divied into ten parts) on Dropbox: P1, P2, P3, P4, P5, P6, P7, P8, P9, P10

Figure 2:Gallery of spherical parameterizations of selected 15 models.
Bibtex
@article {Hu-2017-AHSP,
title = {Advanced Hierarchical Spherical Parameterizations},
author = {Xin Hu and Xiao-Ming Fu and Ligang Liu},
journal = {IEEE Transactions on Visualization and Computer Graphics},
volume = {24},
number = {6},
pages = {1930-1941},
year = {2017},
}