Research
In general, I am interested in designing efficient and provable algorithms for solving real world problems. My primary research area is computational geometry, in particular on geometric optimization algorithms in high dimensions. We can often see trends or clusters in data by graphing or plotting-- giving geometric form to data. As data increases in volume and complexity, giving it geometric form and then developing computational geometry algorithms is still a fruitful way to approach data analysis. For example, activity data from a smartphone or fitness tracker can be viewed as a point in thousands of dimensions whose coordinates include all positions, heart rates, etc. from an entire sequence of measurements. For better privacy, we can share summaries (rough position, duration, etc.) as points in tens of dimensions. Points from many people can be clustered to identify similar patterns, and patterns matched (with unreliable data identified and discarded) to recognize actions that a digital assistant could take to improve quality of life or health outcomes. Below, we briefly show some examples and the results obtained from our research.
Example 1: Clustering
Clustering is one of the most fundamental problems in computer science, and finds numerous applications in many different areas, such as data management, machine learning, bioinformatics, networking. The common goal of many clustering problems is to partition a set of given data items into a number of clusters so as to minimize the total cost measured by a certain objective function. For example, the popular k-means clustering seeks k mean points to induce a partition of the given data items so that the average squared distance from each data item to its closest mean point is minimized. However, in many real-world applications, data items are often constrained or correlated, which require a great deal of effort to handle such additional constraints. In recent years, considerable attention has been paid to various types of constrained clustering problems, such as l-diversity clustering, r-gather clustering, capacitated clustering, fair clustering. One key property exhibited in many unconstrained clustering problems is the so called locality property, which indicates that each cluster is located entirely inside the Voronoi cell of its center. Existing algorithms for these clustering problems often rely on such a property. However, due to the additional constraints, the locality property may no longer exist. We present a unified framework called Peeling-and-Enclosing (PnE), based on two standalone geometric techniques called Simplex Lemma and Weaker Simplex Lemma, to solve a class of constrained clustering problems without the locality property in Euclidean space, where the dimensionality of the space could be rather high.
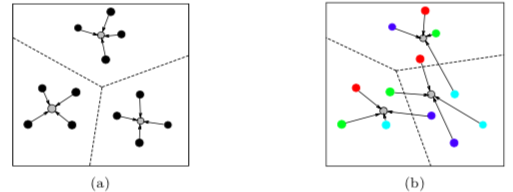
The locality property is destroyed if data items are constrained.
Related publications:
- H. Ding and J. Xu, "A Unified Framework for Clustering Constrained Data without Locality Property", Proc. 26th ACM-SIAM Symposium on Discrete Algorithms (SODA'15), pp.1471-1490, San Diego, CA, USA, January 4-6, 2015.
- H. Ding and J. Xu, "Solving the Chromatic Cone Clustering Problem via Minimum Spanning Sphere" Proc. 38th International Colloquium on Automata, Languages and Programming (ICALP'11), pp.773-784, Z\"{u}rich, Switzerland, July 4-8, 2011.
- H. Ding, L. Hu, L. Huang, and J. Li, "Capacitated Center Problems with Two-Sided Bounds and Outliers" The 15th International Algorithms and Data Structures Symposium (WADS'17), pp.325-336, St. John's, Canada, July 31-August 2, 2017.
- H. Ding, Y. Liu, L. Huang, and J. Li, " K-Means Clustering with Distributed Dimensions" The 33rd International Conference on Machine Learning (ICML'16), pp.1339-1348, New York City, NY, USA, June 19-24, 2016.
Example 2: Geometric Matching and Alignment
Given two patterns in Euclidean space, where each pattern is represented by a (weighted) point set, the goal of geometric matching is to compute the mapping between them with the smallest matching cost (e.g., Hausdorff distance or Earth Mover’s Distance). If the point sets are not fixed the space, the problem is called "geometric alignment" which aims to find appropriate transformations (e.g., rigid or affine transformation) and minimize the matching cost simultaneously. Geometric matching and alignment are fundamental optimization problems, and find many applications in real world, such as face recognition, fingerprint alignment. Moreover, as the recent developments of representation learning theory, a number of machine learning problems can be embedded into Euclidean spaces and reduced to geometric alignment, such as network alignment and unsupervised bilingual learning. We provide a Fully Polynomial Time Approximation Scheme (FPTAS) for solving the geometric alignment problem under rigid transformation.
We also study a new geometric optimization problem called the "geometric prototype'' in Euclidean space. Given a set of point sets, the geometric prototype can be viewed as the "average pattern'' minimizing the total matching cost to them. As a general model, the problem finds many applications in real-world, such as Wasserstein barycenter and ensemble clustering. To our best knowledge, the general geometric prototype problem has yet to be seriously considered by the theory community. To bridge the gap between theory and practice, we show that a small core-set can be obtained to substantially reduce the data size. Consequently, any existing heuristic or algorithm can run on the core-set to achieve a great improvement on the efficiency.
Related publications:
- H. Ding and J. Xu, "FPTAS for Minimizing the Earth Mover's Distance Under Rigid Transformations and Related Problems" Algorithmica, Volume 78, Issue 3, July 2017, pp.741-770.
- H. Ding and M. Ye, "On Geometric Alignment in Low Doubling Dimension'' The 33rd AAAI Conference on Artificial Intelligence (AAAI'19), pp.1460-1467, Honolulu, Hawaii, USA, Jan 27-Feb 1, 2019.
- H. Ding and M. Liu, "On Geometric Prototype and Applications'' The 26th Annual European Symposium on Algorithms (ESA'18), pp.23:1-23:15, Helsinki, Finland, Aug 20-22, 2018.
- Y. Liu, H. Ding, D. Chen, and J. Xu, "Novel Geometric Approach for Global Alignment of PPI Networks" The 31st AAAI Conference on Artificial Intelligence (AAAI'17), pp.31-37, San Francisco, CA, USA, February 4-9, 2017.
- H. Ding, L. Su, and J. Xu, "Towards Distributed Ensemble Clustering for Networked Sensing Systems: A Novel Geometric Approach" The 17th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc'16), pp.1-10, Paderborn, Germany, July 4-8, 2016.
- H. Ding and J. Xu, "Finding Median Point-Set Using Earth Mover's Distance" Proc. 28th AAAI Conference on Artificial Intelligence (AAAI'14), pp.1781-1787, City, Canada, July 27 -31, 2014.
Example 3: Outlier Removal and Robust Optimization
In this big data era, we are confronted with an extremely large amount of data and it is important to develop efficient algorithmic techniques to handle the arising realistic issues. Due to its recent rapid development, machine learning becomes a powerful tool for many emerging applications; meanwhile, the quality of training dataset often plays a key role and seriously affects the final learning result. For example, we can collect tremendous data (e.g., texts or images) through the internet, however, the obtained dataset often contains a significant amount of outliers. Since manually removing outliers will be very costly, it is very necessary to develop some efficient algorithms for recognizing outliers automatically in many scenarios. Outlier recognition is a typical unsupervised learning problem and the given data are unlabeled; thus we can only model it as an optimization problem based on some reasonable assumption in practice. For instance, it is very natural to assume that the inliers (i.e., normal data) locate in some dense region while the outliers are scattered in the feature space. We study several fundamental optimization problems with outliers, such as clustering, classification, and linear regression, and design provable algorithms for them.
Related publications:
- H. Ding: Minimum Enclosing Ball Revisited: Stability and Sub-linear Time Algorithms. CoRR abs/1904.03796 (2019)
- H. Ding, Haikuo Yu A Practical Framework for Solving Center-Based Clustering with Outliers. CoRR abs/1905.10143 (2019)
- H. Ding, H. Yu, and Z. Wang, "Greedy Strategy Works for k-Center Clustering with Outliers and Coreset Construction'' The 27th Annual European Symposium on Algorithms (ESA'19), pp.40:1-40:16, Munich/Garching, Germany, September 9-11, 2019
- H. Ding and J. Xu, "Random Gradient Descent Tree: A Combinatorial Approach for SVM with Outliers" Proc. 29th AAAI Conference on Artificial Intelligence (AAAI'15), pp.2561-2567, Austin, Texas, USA, January 25-30, 2015.
- H. Ding and J. Xu, "Sub-linear Time Hybrid Approximations for Least Trimmed Squares Estimator and Related Problems" Proc. 30th ACM Symposium on Computational Geometry (SoCG'14), pp.110-119, Kyoto, Japan, June 08 - 11, 2014.
Example 4: Application in Crowdsourcing
Truth Discovery is an important problem arising in data analytics related fields such as data mining, database, and big data. It concerns about finding the most trustworthy information from a dataset acquired from a number of unreliable sources. Due to its importance, the problem has been extensively studied in recent years and a number techniques have already been proposed. However, all of them are of heuristic nature and do not have any quality guarantee. We formulate the problem as a high dimensional geometric optimization problem, called Entropy based Geometric Variance. Relying on a number of novel geometric techniques (such as Log-Partition and Modified Simplex Lemma), we further discover new insights to this problem. We show, for the first time, that the truth discovery problem can be solved with guaranteed quality of solution. Particularly, we show that it is possible to achieve a (1+eps)-approximation within nearly linear time under some reasonable assumptions. We expect that our algorithm will be useful for other data related applications.
Related publications:
- Z. Huang, H. Ding, and J. Xu, "A Faster Algorithm for Truth Discovery via Range Cover" Algorithmica Volume 81, Issue 10, October, 2019, pp. 4118-4133.
- H. Ding, J. Gao, and J. Xu, " Finding Global Optimum for Truth Discovery: Entropy Based Geometric Variance" The 32nd International Symposium on Computational Geometry (SoCG'16), 34:1-34:16, Boston, MA, USA, June 14-18, 2016.
- C. Meng, W. Jiang, Y. Li, J. Gao, L. Su, H. Ding, and Y. Cheng, " Truth Discovery on Crowd Sensing of Correlated Entities", The 13th ACM Conference on Embedded Networked Sensor Systems (SenSys'15), pp.169-182, Seoul, South Korea, November 1-4, 2015.
Example 5: Application in Biomedical Imaging
Computing accurate and robust organizational patterns of chromosome territories inside the cell nucleus is critical for understanding several fundamental genomic processes, such as co-regulation of gene activation, gene silencing, X chromosome inactivation, and abnormal chromosome rearrangement in cancer cells. The usage of advanced fluorescence labeling and image processing techniques has enabled researchers to investigate interactions of chromosome territories at large spatial resolution. The resulting high volume of generated data demands for high-throughput and automated image analysis methods. We introduce a novel algorithmic tool for investigating association patterns of chromosome territories in a population of cells. Our method takes as input a set of graphs, one for each cell, containing information about spatial interaction of chromosome territories, and yields a single graph that contains essential information for the whole population and stands as its structural representative. We formulate this combinatorial problem as a semi-definite programming and present novel geometric techniques to efficiently solve it.
Related publications:
- H. Ding, B. Stojkovic, R. Berezney, and J. Xu, "Gauging Association Patterns of Chromosome Territories via Chromatic Median" Proc. IEEE Conference on Computer Vision and Pattern Recognition (CVPR'13), pp.1296-1303, Portland, OR, USA, June 23-28, 2013. Oral presentation (acceptance rate: 3.2%).
- H. Ding, R. Berezney, and J. Xu, "k-Prototype Learning for 3D Rigid Structures" Advances in Neural Information Processing Systems (NIPS'13), pp.2589-2597, Lake Tahoe, Nevada, USA, December 5-8, 2013.
- N. Sehgal, B. Seifert, H. Ding, Z. Chen, B. Stojkovic, S. Bhattacharya, J. Xu, and R. Berezney, "Reorganization of the interchromosomal network during keratinocyte differentiation"Chromosoma, Volume 125, Number 3, June 2016, pp.389-403.
- N. Sehgal, A. Fritz, J. Vecerova, H. Ding, Z. Chen, B. Stojkovic, S. Bhattacharya, J. Xu, and R. Berezney, "Large Scale Probabilistic 3-D Organization of Human Chromosome Territories" Human Molecular Genetics, Volume 25, Number 3, February 2016, pp.419-436. (Awarded Cover Page, and recommended by F1000Prime as an Article of Special Significance to its Field)
- A. Pliss, A. J. Fritz, B. Stojkovic, H. Ding, L. Mukherjee, S. Bhattacharya, J. Xu, and R. Berezney, "Non-random Patterns in the Distribution of NOR-bearing Chromosome Territories in Human Fibroblasts: A Network Model of Interactions'' Journal of Cellular Physiology, Volume 230, Issue 2, February 2015, pp.427-439. (Awarded Cover Page)
- A. J. Fritz, B. Stojkovic, H. Ding, J. Xu, S. Bhattacharya, and R. Berezney, "Cell Type Specific Alterations in Interchromosomal Networks Across the Cell Cycle" PLoS Computational Biology, Volume 10, Issue 10, October 2014.
- A.J. Fritz, B. Stojkovic, H. Ding, J. Xu, S. Bhattacharya, D. Galle, and R. Berezney, "Wide-scale Alterations in Interchromosomal Organization in Breast Cancer Cells: Defining a Network of Interacting Chromosomes" Human Molecular Genetics Volume 23, Number 19, October 2014, pp.5133-5146.