
Geometry curves representation. We represent a 3D shape (right) to a set of planar curves (right), called geometry curves, whose interior lines (shown in yellow) correspond to the feature lines of the surface and the boundary line (shown in red) corresponds to the boundary or fundamental polygon of the surface. The feature lines of geometry curves record the mean curvatures of the 3D shape in both sides which encode the geometry information of the shape. Geometry curves are vectorized forms for 3D shapes which can be used in many applications such as compression, modeling, and editing.
Abstract
We
propose a novel compact surface representation, namely geometry curves,
which record the essence of shape geometry and topology. The geometry
curves mainly contain two parts: the interior and boundary lines. The
interior lines, which correspond to the feature lines, record the
geometry information of the 3D shapes; the boundary lines, which
correspond to the boundary or fundamental polygons, record the topology
information of the 3D shapes. As a vector representation, geometry
curves can depict highly complex geometry details. The concept of
geometry curves can be utilized in many potential applications, e.g.,
mesh compression, shape modeling and editing, animation, and level of
details. Furthermore, we develop a procedure for automatically
constructing geometry curves which obtain an excellent approximation to
the original mesh.
- X. Gu, S. Gortler, H. Hoppe. Geometry images. ACM Transactions on Graphics (Proc. SIGGRAPH), 21(3), 355-361, 2002.
- A. Orzan, A. Bousseau, H. Winnemöller, P. Barla, J. Thollot, D. Salesin. Diffusion curves: a vector representation for smooth-shaded images. ACM Transactions on Graphics (Proc. SIGGRAPH), 27(3), 92:1-8, 2008.
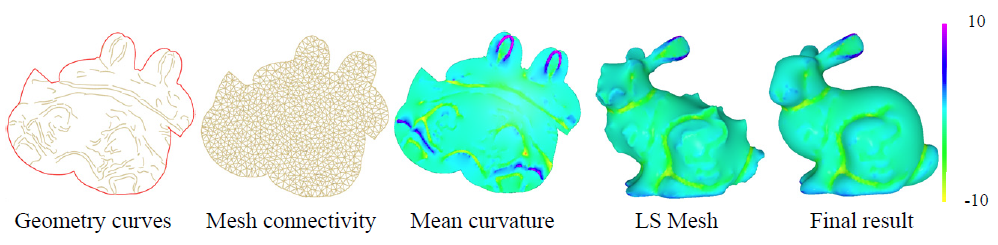
Recovering the surface from geometry curves. (Left to right) Starting from geometry curves, we employ the constrained Delaunay triangulation method to construct the mesh connectivity. After that we diffuse the mean curvature from geometry curves and reconstruct the surface by Poisson equation. The color bar on the right side represents the mean curvature value.

More examples of geometry curves. The below example is the Fandisk model with sharp features. The red lines on surfaces are cut edges.
Thanks
to the reviewers for their constructive comments. Thanks also to Andy Xia for
the video voice recording, Shen Yu, Kun Liu, Haibin Huang and Stephen Giguere
for helpful discussions. This work is supported by the National Natural
Science Foundation of China (61070071, 61222206) and the National Basic
Research Program of China (2011CB302400).
title = {Geometry curves: A compact representation for 3D shapes},
author = {Guo Li and Ligang Liu}
journal = {Graphical Models},
volume = {75},
Issue = {5},
pages = {265-278},
year = {2013}
}