Elasticity of ferropericlase at lower mantle PT condition
Ferropericlase is second abundant mineral at lower mantle. Iron atoms of ferropericlase, which has magnetic moment at ambient pressure, will lose magnetic moment at lower mantle pressure. This transition is called high spin to low spin transition. This study demonstrates that spin transition significantly reduces the bulk modulus but has not such effect on shear modulus because of cubic symmetry of ferropericlase. But if cubic symmetry of ferropericase is broken by non-hydrostatic pressure, spin transition also reduces the shear modulus. This can well explain the discrepancy on shear modulus between two previous experimental measurements. The extrapolation of the experimental shear velocity of ferropericlase to higher temperature and concentration by Murakami et al [2012] introduced large error. The lower mantle composition based on their extrapolation need to be readjusted. Spin transition occurs at broad depth of lower mantle. Its dramatic effect on the elastic modulus must significantly impact our understanding to Earth’s interior. The systematical high pressure and temperature elasticity of ferropericlase obtained by this study will be very useful for us to uncover more the mystery of Earth’s interior.
Spin effect on other properties of ferropericlase has been discussed in Wu et al (2009) and Wentzcovitch et al (2009). Spin transition of ferropericlase on mantle convection has been discussed in Shahnas et al (2011).
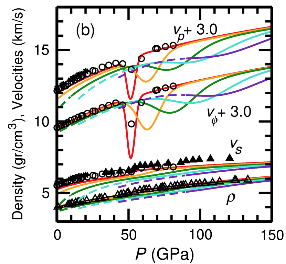
Elasticity of ferropericlase at 300K (red), 1000K (yellow), 2000K (green), 3000K(blue), and 4000K(purple)
An analytical approach for thermal elasticity of crystals
Thermal elastic properties of crystals are defined from second-order derivatives of free energies with respect to strain. In general, this will require calculating free energy under strain. These are exceedingly demanding computations requiring up to ∼103 parallel jobs running on tens or more processors each. Here, we developed an analytical formula to describe second-order derivatives of free energies with respect to strain. This approach decreases the computational effort, i.e., CPU time and human labor, by up to two orders of magnitude because the approach avoids calculating phonon density of states under strain. Results for the major mantle phases periclase (MgO) and forsterite (α-Mg2SiO4) show excellent agreement with previous first-principles results and experimental data.
The approach has been used to calculated the elasticity of olivine, wadsleyite (Valdez et al GRL 2013), ringwoodite (Valdez et al EPSL 2012), and ferropericlase (Wu et al PRL 2013).
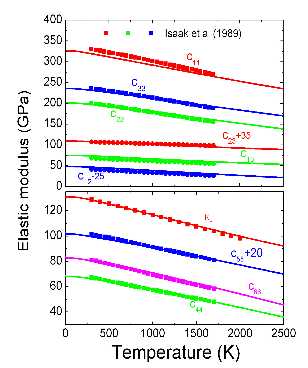
Elasticity of ferropericlase of forsterite
A first principles-based method for anharmonic free energy
We developed a method to compute anharmonic free energy neglected in quasiharmonic calculations by introducing parametrized temperature-dependent modification of the vibrational density of states. The introduced parameter is a constant and can be calculated through a first-principles molecular-dynamics simulation. The thermodynamics properties of forsterite,periclase, and diamond improve considerably after inclusion of anharmonic effects.
The method has been used to develop the precise high temperature pressure standard of MgO (Wu et al JGR 2009).
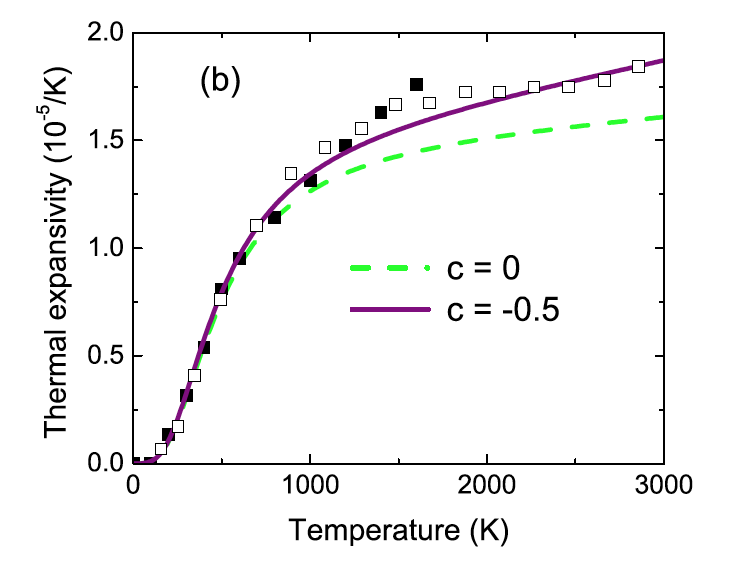
Thermal expansion of diamond with (purple) and without (green) anharmonic correction.
Equilibrium fractionation factors of Mg among major upper mantle minerals
Equilibrium fractionation factors of Mg isotopes at high temperature and pressure are investigated for pyrope,majorite,clinopyroxene,orthopyroxene,andolivine using density functional theory. The results reveal significant inter- mineral Mg isotope fractionations due to different coordination environment of Mg in minerals. Specifically,pyrope,where Mg is in eight-fold coordination,is more enriched in light Mg isotopes than olivine and pyroxene where Mg is in six-fold coordination.The calculated isotope fractionation for Mg isotopes between clinopyroxene and pyrope is consistent with observations from natural eclogites (Li etal.,2011; Wang etal.,2012). Our calculation also reveals substantial pressure effect onMg isotope fractionations among garnet,pyroxene,and olivine. Equilibrium fractionation of Mg isotopes between pyrope and pyroxene(and olivine) could be used as a novel and independent thermometry with precision much better than the traditional garnet– clinopyroxene Fe Mg exchange thermometry because such fractionation is significantly greater than the current uncertainties of Mg isotope analyses. These Mg isotope thermometries could have wide applications in high-temperature mafic igneous and metamorphic rocks where garnet co-exists with pyroxene or olivine.
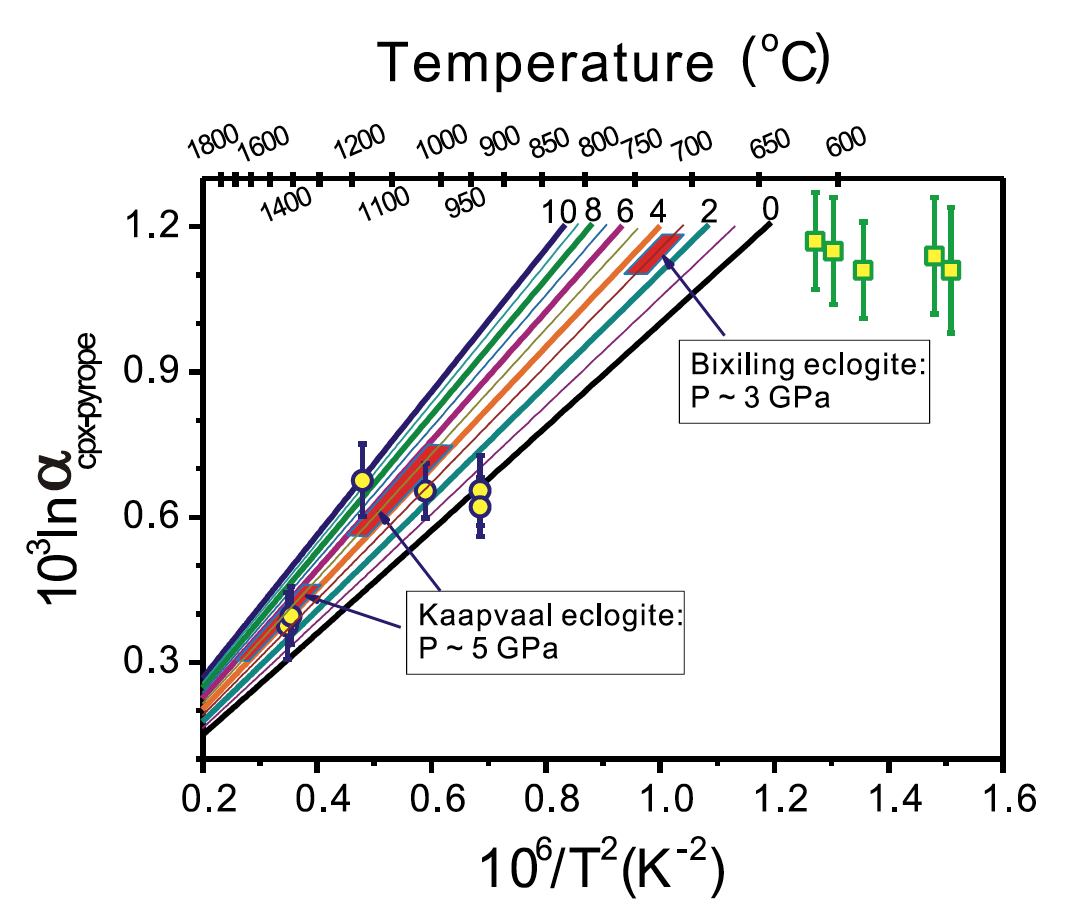
Application of clinopyroxene–garnet Mg isotope thermometry to estimating equilibrium temperature of eclogites.