

Helsinki, April 19, 1999
Data Structures Project
University of Helsinki
Department of Computer Science
Tutor: Timo Patrikka
Contents
1 Instructions for Use
1.1 Introduction
1.2 Installation and Compilation
1.3 Using the Program
1.4 Limitations2 Program Structure
2.1 About the Knight's Tour Quandary
2.2 The Algorithm
2.3 Class Structure
2.3.1 KnightsTour
2.3.2 KnightThread
2.3.3 GraphicalBoard
2.3.4 BoardListener
2.3.5 KnightBoard
2.4 Possible improvements3 Testing
3.1 Testing Tool
3.2 Verifying Individual Classes
3.3 Test Results
1 Instructions for Use
1.1 Introduction
The knight's tour is a puzzle that has amused chess players throughout the ages. The goal of the knight is to traverse around the board, landing on each square but once, and finally return to the square it started from. If the board is thought of as a graph, this kind of closed path is called a Hamiltonian cycle. It can be proven that there is a closed knight's tour on all boards with an even number of squares and dimensions greater than four.The Knight's Tour Applet demonstrates a simple algorithm for finding a knight's tour. The idea is to always jump to the square with least exits, unless that makes some unvisited squares unreachable. This algorithm works surprisingly well: in the majority of cases the program chooses the right moves on first try, without having to back up once. If this fails, all possibilities are eventually tried in a depth-first manner.
The program is implemented as a Java applet that can be run with any browser that supports Java 1.1. The board is represented graphically, and can be resized by dragging the borders with the mouse to any dimensions between five and ten. The starting square can be chosen freely, and the actual search process can be viewed as an animation or skipped to just see the final solution.
1.2 Installation and Compilation
The program is an applet that can be run with either a Java 1.1-capable browser, such as Netscape Navigator 4.06 or newer, or the applet viewer that comes with Sun Microsystem's Java Development Kit (JDK). The easiest way to try the program is to enable Java in the browser settings and point it to the following URL: http://www.helsinki.fi/~vahaaho/KnightsTour/tour.html.If you have JDK 1.1 or later installed, you may also download the program along with the source code as a gzip'd tar package from http://www.helsinki.fi/~vahaaho/KnightsTour/knightstour.tar.gz. The package contains the following files:
Makefile
BoardListener.java
GraphicalBoard.java
KnightBoard.java
KnightThread.java
KnightsTour.java
Test.javadoc/
doc.html
overview.html
...
images/
...Details of how to install and compile vary, but on Linux and other Unix systems the following shell commands will do the job:
tar -xzvf knightstour.tar.gzThe program and documentation are freely distributable and modifiable as long as credit is given to the original author.
cd KnightsTour
make
appletviewer tour.html1.3 Using the Program
The applet presents a friendly graphical user interface that should be very easy to use. First, the program asks to choose the starting square. Use the mouse to click on a square of your choice. The program then starts to look for a solution:
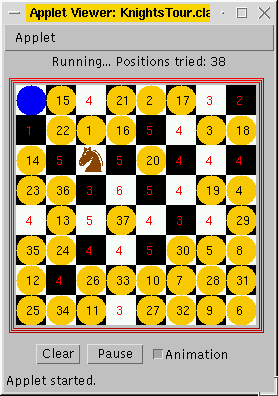
Figure 1. Program running.
The starting square is shown with a filled blue circle. The current position of the knight has a knight image in it, and already visited squares have yellow circles containing the number of the move. Unvisited squares have a number printed in red that tells how many exits the square has left; the program chooses the square with least exits first. If the search comes to a dead end, the knight backs up one move at a time. When the search is completed, the total number of positions tried is shown.
The process can be paused with the 'Pause' button and resumed by selecting the same button again. Animation can be switched on and off using the checkbox, and the board cleared with the 'Clear' button. If the search process is lengthy or not of interest, it is a good idea to switch off animation.
When searching is not going on, the board can be resized. Moving the cursor over the right or bottom borders changes its shape, meaning that the borders may be dragged by pressing and holding the mouse button and moving the mouse. During dragging, the number of squares in the board is shown in the upper left corner. If the number is odd, it is printed in red, because there are no solutions for such boards. After the drag, the board is automatically cleared.
The program has been tested to find solutions for all even-sized boards from all starting squares, as should be the case. On symmetrical even-sized boards the number of positions tried is usually small, but on a 5x6 board, for example, tens of thousands may be needed. On odd-sized boards the number of positions the program has to go through before quitting is very large, except for the 5x5 board, where it lies between 15 000 and 40 000. By switching off animation, this can be verified even on slower computers. For more detailed figures, see section 3.3.
1.4 Limitations
Currently, the dimensions of the board can only be between five and ten. There are solutions for some boards three squares wide, but not for one, two, or four wide. The upper bound of ten is to always leave sufficient space for the user to resize the board without making the individual squares too small. It is possible to change these bounds by changing constants in the classes KnightBoard and GraphicalBoard.There is no way to save or print the intermediate or final results.
2 Program Structure
2.1 About the Knight's Tour Quandary
From Ted Feller's Knight's Tour page (after Scientific American, May 1997):Mathematically, the knight's tour quandary reduces to finding a "Hamiltonian cycle" in a graph. A graph is a collection of dots, called nodes, joined by lines, called edges. A Hamiltonian cycle is a closed path that visits each node exactly once. The graph of a chessboard is obtained by placing a node at the center of each square and then drawing edges between nodes that are separated by one knight's move. It helps to color the nodes dark and light, corresponding to the usual pattern on a chessboard. Notice that when the knight moves, it hops from a node of one color to one of the opposite color, so the nodes must be alternately dark and light around any Hamiltonian cycle. This pattern implies that the total number of nodes must be even. If the chessboard were 3 x 5, with 15 nodes (an odd number), we have proved that no knight's tour is possible on such a chessboard. The same is true for any rectangular board of size m x n where m and n are both odd.
Figure 2. Knight's moves. Figure 3. Knight's graph. This kind of argument is known as a parity proof. A more subtle parity proof, invented by Louis Posa, demonstrates that there is no closed knight's tour on any 4 x n board. Allen Schwenk provided a characterization of those rectangular boards that support a knight's tour. He found that an m x n chessboard (when m is less than or equal to n) supports a knight's tour unless:
The key idea is that a tour on an m x n board can always be extended to one on an m x (n + 4) rectangle. By symmetry, a tour on an m x n board can be extended to any (m + 4) x n rectangle.m and n are both odd m = 1, 2 or 4 m = 3 and n = 4, 6 or 8 2.2 The Algorithm
The algorithm used is very simple. When a new board is created, a value is calculated for each square. This value represents the number of exits, ie. the number of unvisited squares reachable in one move. An adjacency list is created for each square, which contains indices to the squares reachable directly from it.The tour is looked for using a recursive function that implements a depth-first search. Possible moves are tried in order of increasing value, so the squares with the least number of exits come first. This is known as Warnsdorff's rule. If there are many squares with the same value, they are tried in order of decreasing distance from the starting square.
After each move, the values for all affected squares are updated, and the square is marked visited. The starting square is not actually visited until last, so special care is taken of the squares adjacent to it in the graph. No move that is not next-to-last may use the last unvisited one. This way, the program ensures there is always at least one way back to the starting square. Also, each time values are updated, orphaned (unreachable) squares are checked for. If a move would result in unreachable squares, it is skipped. This decreases the total size of the search tree considerably.
2.3 Class Structure
The class structure of the program is as follows:

Figure 4. UML class diagram.
Only a single object of each class exists at a time. Description of the classes follows.
JavaDoc class tree JavaDoc index of names 2.3.1 KnightsTour
This is the main class, a subclass of java.applet.Applet. It instantiates a GraphicalBoard and a KnightThread, and passes the board to the newly created thread. It takes care of handling user actions, receiving events from the AWT as well as the GraphicalBoard by implementing the BoardListener interface. A new board and thread are created every time the board is cleared.
JavaDoc documentation Source code 2.3.2 KnightThread
A KnightThread does the actual searching. After it is instantiated, it must be given a start square and then started. At the core is the recursive function solution() that is called for each new knight position. Moves are made in solution() using KnightBoard services. The thread also takes care of having pauses between steps and refreshing the display if animation is enabled.
JavaDoc documentation Source code 2.3.3 GraphicalBoard
Adds a graphical representation to KnightBoard, which it subclasses. It is also a subclass of java.awt.Canvas via KnightBoard. The update() method draws the board on screen, adjusting to the amount of screen space available. Subsequently, it re-draws only the squares whose content has changed. The class also handles its own mouse events, calling a BoardListener when the user clicks or drags the board.
JavaDoc documentation Source code 2.3.4 BoardListener
Interface for receiving boardClicked() and boardResized() events from GraphicalBoard.
JavaDoc documentation Source code 2.3.5 KnightBoard
Provides a rectangular chess board of freely chosen size with services for finding a knight's tour. Though it appears to subclass java.awt.Canvas, it does not use any Canvas services and is not a graphical object. Because Java does not support multiple inheritance, this is a kludge to allow GraphicalBoard to subclass Canvas. The board keeps track of the values of the squares, of the moves made, and provides adjacency lists for the squares. The values are updated automatically when moves are made using moveKnight() and undone using undoMove().The Makefile of the program supports generating JavaDoc documentation with the command 'make doc'.The adjacency lists are stored in a four-dimensional array. The first two dimensions specify the x- and y-indices of the squares, as usual. The third enumerates the adjacent (reachable) squares, of which there can be at most eight. The fourth gives the x- and y-indices of the adjacent squares in indices 0 and 1, respectively. This is faster and uses less memory than a linked list, since the number of elements is bounded and small. The public method getAdjacencyList() gives the list for a specified square.
Invariant() is a quite complete test for the validity of the board state. Because of its completeness, it is too slow to be called each time a move is made except when debugging. However, it is used to verify the validity of the board before starting and after finding a solution. If it returns false, which should never be the case, the program terminates immediately on an exception.
Specifically, Invariant() first checks that the class variables of the board object are non-null. It then proceeds to check that there is exactly one start square, count the number of moves on the board, calculate the values of all squares, and compare them to the ones stored in the class variables. If the tour is finished, it also makes sure that the moves are legal and in correct order.
JavaDoc documentation Source code 2.4 Possible Improvements
An obvious area for improvement is the algorithm. Although the average-case running time is excellent, measured experimentally to be linear in the number of squares, the worst case is exponential. In contrast, there is a simple divide-and-conquer algorithm that can be used on symmetrical boards of dimensions greater than five, whose worst-case running time has an upper bound linear in the number of squares.An useful improvement would be to be able to save intermediate steps and the final tour to disk for analysis and storage. Also interesting might be to be able to time the process and change some parameters of the algorithm on the fly to see how it affects performance.
3 Testing
3.1 Testing Tool
To aid in testing, a short, independent Java program imaginatively called 'Test' has been written. To use it, JDK 1.1 or later must be properly installed. It can be compiled with the command 'make test' and run with 'java Test'. Optionally, the dimensions of the board may be given as parameters, as in 'java Test 6 8', which uses a 6x8 board. The default dimensions are 8x8. Note that there is no upper bound on the board dimensions.The test program runs KnightThread using each square on the board in turn as the starting square, and prints the number of steps that were needed to find a solution in each case to the console. If all is well, either a solution will be found for all starting squares or, for odd-sized boards, none will be found for any of them. Verifying the latter case usually takes too much time (except on a 5x5 board), since the algorithm does not give up until all knight positions have been tried.
The test program itself is not fool-proof or user-friendly, since it is only intended for development. Test results are given in section 3.3.
Source code 3.2 Verifying Individual Classes
At the core of the program is the KnightBoard class. Because its correctness is vital, a complete invariant test has been incorporated into the class, as described in section 2.3.5. The program has been extensively tested using the Test program with the invariant check done after each move; no failures occurred (see section 3.3).The correctness of the algorithm in KnightThread is more difficult to prove. It can be argued that since it is a depth-first search that checks all possibilities, it will always find a tour if one exists or stop after an exhaustive search. According to the tests this indeed seems to be the case. All tours produced by the program were correct, as verified by the invariant in KnightBoard and some even checked by hand.
The remaining classes provide the user interface. Besides being intuitive, the graphical interface also makes it impossible for the user to enter invalid values. It has been thoroughly tested in practice by the author and some of his friends on a Linux-based JDK 1.1.7 platform as well as on Netscape Navigator 4.08. Since these classes are also structurally simple, they can, on the basis of these tests, be considered fault-free.
3.3 Test Results
The test program was completed for the following board sizes: 5x5 (no solutions), 5x6, 5x8 (*), 5x10 (*), 6x6, 6x8, 7x8, 8x8, 8x10, 10x10. On all boards except 5x5 a solution was found for every starting square. The tests were also run with the KnightBoard invariant check done after each move except for the boards marked with an asterisk (*), which took exceptionally long to complete. No problems arose in any of the tests.Some verbatim logs of timed tests are below. Times are wall clock times measured on a dedicated Pentium II-300 MHz running JDK 1.1.7 with Tya 1.2v4 just-in-time compiler on Linux 2.2.5. The invariant check was not done between moves. The coordinates on the left mark the x and y coordinates of the starting square, so that (0, 0) corresponds to a1.
Starting test on a board of size 5x5...Running the test for a standard 8x8 chess board takes about 1.5 seconds, and a solution is found for all but two squares in 64 steps - the two take 117 steps. A 10x10 board takes 4 seconds to complete. For the largest one tried, 150x150, finding one solution from a1 takes 20 seconds and 22 500 steps. As can be seen from these figures, average-case performance is nearly optimal. Generally, for boards with dimensions of at least eight solutions are found very quickly. Some small asymmetrical boards present problems to our algorithm: from some starting squares tens of millions of steps may be needed before a tour is found.
(0, 0): No solution found; 23251 positions tried.
(0, 1): No solution found; 40777 positions tried.
(0, 2): No solution found; 36367 positions tried.
(0, 3): No solution found; 40777 positions tried.
(0, 4): No solution found; 23251 positions tried.
(1, 0): No solution found; 40777 positions tried.
(1, 1): No solution found; 36563 positions tried.
(1, 2): No solution found; 15459 positions tried.
(1, 3): No solution found; 36563 positions tried.
(1, 4): No solution found; 40777 positions tried.
(2, 0): No solution found; 36367 positions tried.
(2, 1): No solution found; 15459 positions tried.
(2, 2): No solution found; 19601 positions tried.
(2, 3): No solution found; 15459 positions tried.
(2, 4): No solution found; 36367 positions tried.
(3, 0): No solution found; 40777 positions tried.
(3, 1): No solution found; 36563 positions tried.
(3, 2): No solution found; 15459 positions tried.
(3, 3): No solution found; 36563 positions tried.
(3, 4): No solution found; 40777 positions tried.
(4, 0): No solution found; 23251 positions tried.
(4, 1): No solution found; 40777 positions tried.
(4, 2): No solution found; 36367 positions tried.
(4, 3): No solution found; 40777 positions tried.
(4, 4): No solution found; 23251 positions tried.
Test finished.
Elapsed time: 34 seconds.Starting test on a board of size 6x6...
(0, 0): Solution found; 36 positions tried.
(0, 1): Solution found; 36 positions tried.
(0, 2): Solution found; 525 positions tried.
(0, 3): Solution found; 525 positions tried.
(0, 4): Solution found; 36 positions tried.
(0, 5): Solution found; 36 positions tried.
(1, 0): Solution found; 36 positions tried.
(1, 1): Solution found; 40 positions tried.
(1, 2): Solution found; 36 positions tried.
(1, 3): Solution found; 36 positions tried.
(1, 4): Solution found; 36 positions tried.
(1, 5): Solution found; 36 positions tried.
(2, 0): Solution found; 41 positions tried.
(2, 1): Solution found; 36 positions tried.
(2, 2): Solution found; 36 positions tried.
(2, 3): Solution found; 36 positions tried.
(2, 4): Solution found; 36 positions tried.
(2, 5): Solution found; 41 positions tried.
(3, 0): Solution found; 41 positions tried.
(3, 1): Solution found; 36 positions tried.
(3, 2): Solution found; 36 positions tried.
(3, 3): Solution found; 36 positions tried.
(3, 4): Solution found; 36 positions tried.
(3, 5): Solution found; 41 positions tried.
(4, 0): Solution found; 36 positions tried.
(4, 1): Solution found; 40 positions tried.
(4, 2): Solution found; 36 positions tried.
(4, 3): Solution found; 36 positions tried.
(4, 4): Solution found; 36 positions tried.
(4, 5): Solution found; 36 positions tried.
(5, 0): Solution found; 36 positions tried.
(5, 1): Solution found; 36 positions tried.
(5, 2): Solution found; 525 positions tried.
(5, 3): Solution found; 525 positions tried.
(5, 4): Solution found; 36 positions tried.
(5, 5): Solution found; 36 positions tried.
Test finished.
Elapsed time: 1 second.On the test system the program examines about 10 000 to 20 000 positions per second on small boards. If we estimate the branching factor for a 7x7 board to be at least 1.6, the number of all possible knight positions exceeds 1.6^49, about ten billion. This rules out the possibility of experimentally verifying the absence of tours for (odd-sized) boards larger than 5x5.