|
Construction of Manifolds
ACM Transactions on Graphics,
35(2), Article 14: 1-10, 2016.
|
|||||||
|
|
|||||||
|
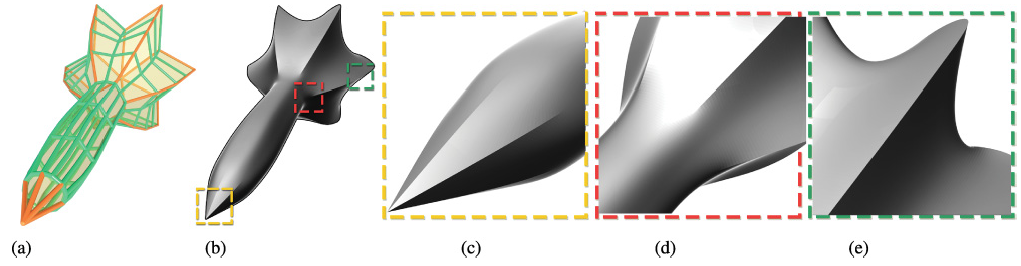
Teaser: From a mesh (a), our approach generates a manifold surface (b) approximating its Catmull-Clark subdivision surface. Sharp features are created in the subdivision surface by enforcing C0 constraints on edges in red (a). The constructed manifold (b) approximates various features like crease, dart, and cusp well. The regions in red, green, and blue are zoomed and shown in (c), (d), and (e), respectively.
|
|||||||
| Abstract |
Manifold is an important technique to model
geometric objects with arbitrary topology. In this article, we propose a
novel approach for constructing manifolds from discrete meshes based on
sparse optimization. The local geometry for each chart is sparsely
represented by a set of redundant atom functions, which have the
flexibility to represent various geometries with varying smoothness. A
global optimization is then proposed to guarantee compatible sparse
representations in the overlapping regions of different charts. Our
method can construct manifolds of varying smoothness including sharp
features (creases, darts, or cusps). As an application, we can easily
construct a skinning manifold surface from a given curve network.
Examples show that our approach has much flexibility to generate
manifold surfaces with good quality.
|
||||||
| Keywords |
Manifold, Sharp feature, Sparse
representation, Curve network
|
||||||
| Concept |
Definition of a manifold:
Manifold modeling is a technology used to construct surfaces from a
domain manifold. The domain manifold is covered by a collection of
charts with overlapping regions. The local mapping is a one-to-one map
(parameterization) from one chart to an open set in the plane domain,
which defines the local coordinate system for the chart. If two charts
overlap, the transition function describes the transformation between
them. |
||||||
| Overfitting Problem |
Given a set of sampling points (100 points in total) from a C0 surface (a), the obtained fitting surface via polynomials (b), redundant atom functions (c), and sparse representation (d). (e) The first five atom functions (C0 shape functions in red boxes and polynomials in gray boxes) selected in the sparse representation. The sparsity is set at 25. |
||||||
| Results |
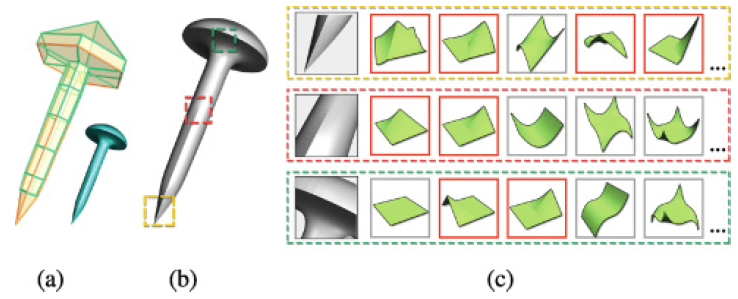
Constructing manifold to approximate subdivision surface. (a) The input control mesh with enforced C0 features shown in red. (b) The manifold generated by our approach. (c) The close-up views of three parts of sharp features including crease, dart, and cusp. The first five atom functions that are adaptively selected for representing the local features are shown.
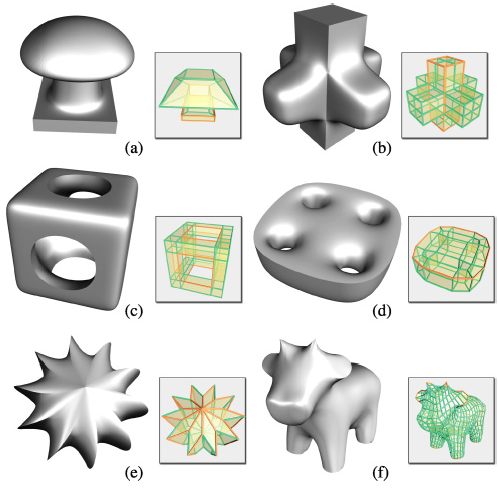
Examples of manifolds constructed by our approach to approximate the subdivision surfaces with given control meshes in the lower right. C0 constraints shown in red are enforced to created sharp features in the subdivision surfaces. |
||||||
| Paper |
PDF
(1.3M)
|
||||||
| Video |
Demo (*.wmv) (52.0M)
|
||||||
|
Presentation (at SIGGRAPH 2016) |
Fast Forward (0.5M) PPT (2.0M)
|
||||||
| Ack |
We would like to thank the anonymous reviewers for their comments and suggestions. The work is supported by the NSF of China (grants 11171322, 11371341, 11526212, 11571338, and 61222206), the One Hundred Talent Project of the Chinese Academy of Sciences, and the Fundamental Research Funds for the Central Universities (WK0010000051).
|
||||||
| BibTex |
@article {Wang:TOG2016, title = {Construction of Manifolds via Compatible Sparse Representations}, author = {Ruimin Wang and Ligang Liu and Zhouwang Yang and Kang Wang and Wen Shan and Jiansong Deng and Falai Chen} journal = {ACM Transactions on Graphics}, volume={35}, number={2}, pages={Article 14: 1-10}, year = {2016} } |
||||||
|
|
|||||||
|
|
|||||||
| Copyright and disclaimer: The SOFTWARE provided at this page is provided "as is", without any guarantee made as to its suitability or fitness for any particular use. It may contain bugs, so use of this tool is at your own risk. We take no responsibility for any damage that may unintentionally be caused through its use. |
| Copyright © 2015 GCL , USTC |