Introduction
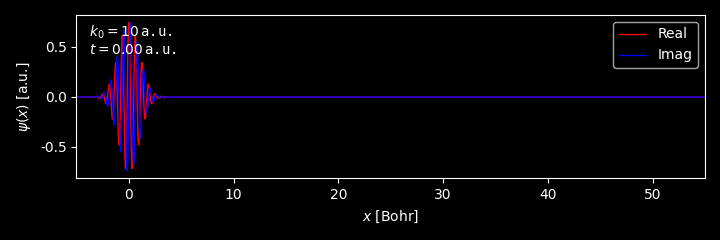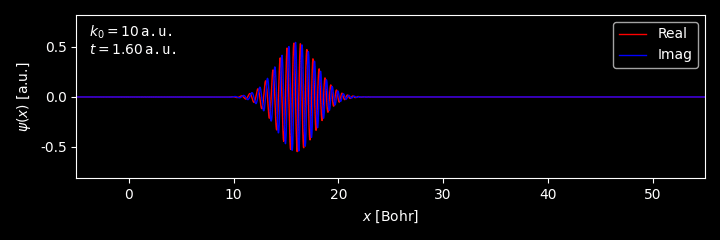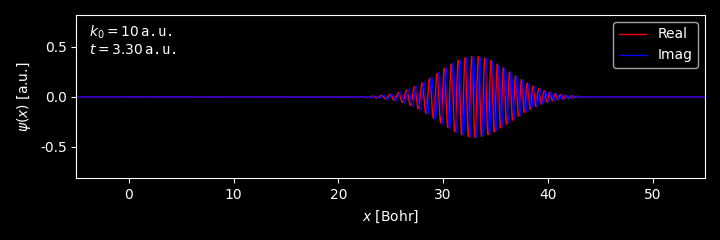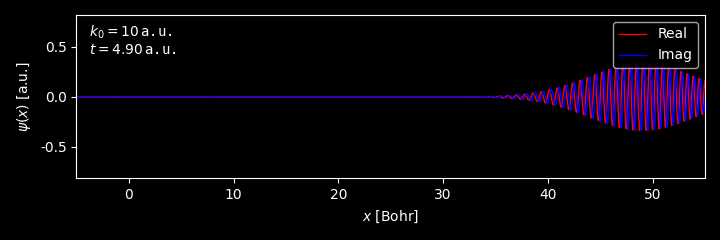
Consider a 1D free particle which is described at $\mathrm{t} = 0$ by the normalized Gaussian wavefunction
\[\begin{equation} \psi(x, t=0) = \left[ \frac{1}{\pi\sigma^2} \right]^{1/4} e^{-x^2/2\sigma^2} e^{ik_0 x} \end{equation}\]How does this wavefunction evolve under the free space Hamiltonian?
\[\begin{equation} \mathcal{H} = -\frac{\hbar^2}{2m}\nabla^2 \label{eq:hamil_free} \end{equation}\]To this end, one can first perform Fourier transform, i.e.
\[\begin{equation} \psi(x, 0) = \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty u(k) e^{ikx} \,\mathrm{d}k \qquad\Longleftrightarrow\qquad u(k) = \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \psi(x, 0) e^{-ikx} \,\mathrm{d}x \end{equation}\]Remember that the plain-waves $e^{ikx}$ are the eigenfunctions of Eq.\eqref{eq:hamil_free}, therefore one can readily write down the time evolution of the 1D wavepacket as
\[\begin{equation} \psi(x, t) = \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty u(k) e^{ikx} \textcolor{red}{ e^{- i\omega_k t} } \,\mathrm{d}k \label{eq:td_gau_form} \end{equation}\]where $\epsilon_k$ is the energy of the plain-wave:
\[\begin{equation} \epsilon_k = \frac{\hbar^2 k^2}{2m} = \hbar\omega_k \end{equation}\]Fourier transform of Gaussian wavepacket
The Fourier transform of the Gaussian wavepacket writes
\[\begin{align} u(k) &= \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \psi(x, 0) e^{-ikx} \,\mathrm{d}x \\ &= \textcolor{black}{ \frac{1}{\sqrt{2\pi}} \left[ \frac{1}{\pi\sigma^2} \right]^{1/4} } \int\limits_{-\infty}^\infty e^{-x^2/2\sigma^2} e^{ik_0x} e^{-ikx} \,\mathrm{d}x \\ &= \textcolor{black}{ \left[ \frac{1}{4\pi^3\sigma^2} \right]^{1/4} } \sqrt{2\pi\sigma^2} \exp\left[ -\frac{ \sigma^2(k - k_0)^2 }{ 2 } \right] \\ &= \textcolor{black}{ \left[ \frac{\sigma^2}{\pi} \right]^{1/4} } \exp\left[ -\frac{ \sigma^2(k - k_0)^2 }{ 2 } \right] \label{eq:gaussian_ft} \end{align}\]where we have used the Gaussian integral listed in the appendix with
\[\begin{align} a & = \frac{1}{2\sigma^2} \\ b & = i[k - k_0]\cdot x \end{align}\]Time evolution of Gaussian wavepacket
Now, substituting Eq.\eqref{eq:gaussian_ft} back into Eq.\eqref{eq:td_gau_form}, one has
\[\begin{align} \psi(x, t) &= \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty u(k) e^{ikx} e^{- i\omega_k t} \,\mathrm{d}k \\ &= \frac{1}{\sqrt{2\pi}} \left[\frac{\sigma^2}{\pi}\right]^{1/4} \int\limits_{-\infty}^\infty e^{-\sigma^2(k - k_0)^2 /2} e^{ikx} e^{- i\omega_k t} \,\mathrm{d}k \\ &= \left[\frac{\sigma^2}{4\pi^3}\right]^{1/4} \sqrt{\frac{\pi}{\sigma^2/2 + \frac{i\hbar t}{2m}}} \, % e^ {-k_0^2\sigma^2/2} % \\ % &\quad % \times \exp\left[ \frac{(ix + \sigma^2k_0)^2}{2\sigma^2 + 2\frac{i\hbar t}{m}} - \frac{k_0^2\sigma^2}{2} \right] \\ &= \left[\frac{\sigma^2}{\pi}\right]^{1/4} \sqrt{\frac{1}{\sigma^2 + \frac{i\hbar t}{m}}} \, \exp\left[ \frac{(ix + \sigma^2k_0)^2}{2\sigma^2 + 2\frac{i\hbar t}{m}} - \frac{k_0^2\sigma^2}{2} \right] \\ &= \left[\frac{\sigma^2}{\pi}\right]^{1/4} \sqrt{\frac{1}{\sigma^2 + \frac{i\hbar t}{m}}} \, \exp\left[ - \frac{ (x - i[\sigma^2 + \frac{i\hbar t}{m} - \frac{i\hbar t}{m}]k_0)^2 } {2\sigma^2 + 2\frac{i\hbar t}{m}} - \frac{k_0^2\sigma^2}{2} \right] \\ &= \left[\frac{\sigma^2}{\pi}\right]^{1/4} \sqrt{\frac{1}{\sigma^2 + \frac{i\hbar t}{m}}} \, \exp\left[ - \frac{ ([x - \frac{\hbar k_0}{m}t] - i[\sigma^2 + \frac{i\hbar t}{m} ]k_0)^2 } {2\sigma^2 + 2\frac{i\hbar t}{m}} - \frac{k_0^2\sigma^2}{2} \right] \\ &= \left[\frac{\sigma^2}{\pi}\right]^{1/4} \sqrt{\frac{1}{\sigma^2 + \frac{i\hbar t}{m}}} \, \exp\left[ - \frac{ (x - \frac{\hbar k_0}{m}t)^2 } {2\sigma^2 + 2\frac{i\hbar t}{m}} \right] \exp\left[ \frac{ i(x - \frac{\hbar k_0}{m}t)k_0 } {2} \right] \\ &\quad \phantom{ \left[\frac{\sigma^2}{\pi}\right]^{1/4} \sqrt{\frac{1}{\sigma^2 + \frac{i\hbar t}{m}}} \, } \times \exp\left[ \frac{ (\sigma^2 + \frac{i\hbar t}{m})k_0^2 } {2} - \frac{k_0^2\sigma^2}{2} \right] \\ &= \left[\frac{\sigma^2}{\pi}\right]^{1/4} \sqrt{\frac{1}{\sigma^2 + \frac{i\hbar t}{m}}} \, \exp\left[ - \frac{ (x - \frac{\hbar k_0}{m}t)^2 } {2\sigma^2 + 2\frac{i\hbar t}{m}} \right] e^{ik_0x} \label{eq:gau_time} \end{align}\]where from the second line to the third line we have used the Gaussian integral with
\[\begin{aligned} a &= \frac{\sigma^2}{2} + \frac{i\hbar t}{2m} \\ b &= ix + \sigma^2 k_0 \end{aligned}\]Average position of the wavepacket
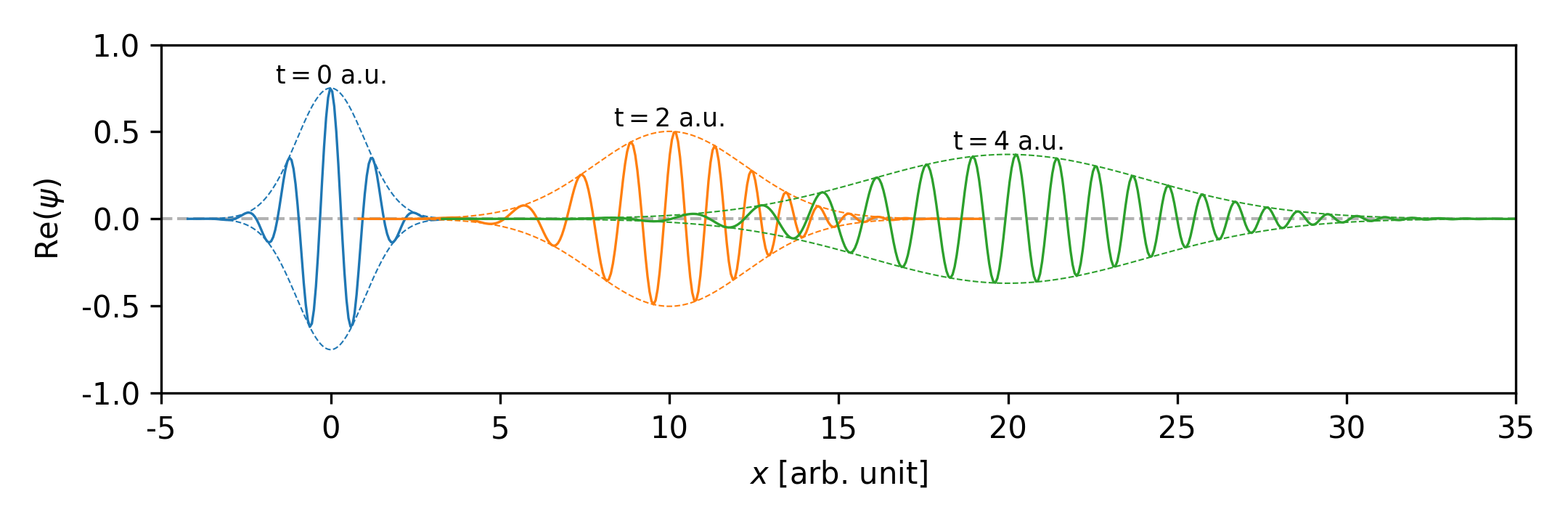
With Eq.\eqref{eq:gau_time}, one can obtain the average position of the wavepacket
\[\begin{align} \langle x \rangle &= \int\limits_{-\infty}^\infty \psi^*(x, t) x \psi(x, t) \mathrm{d}x \\ &= \left[\frac{\sigma^2}{\pi}\right]^{1/2} \sqrt{\frac{1}{\sigma^4 + \frac{\hbar^2 t^2}{m^2}}} \int\limits_{-\infty}^{\infty} \exp\left[ - \frac{ (x - \frac{\hbar k_0}{m}t)^2 } {2\sigma^2 - 2\frac{i\hbar t}{m}} \right] [x] \exp\left[ - \frac{ (x - \frac{\hbar k_0}{m}t)^2 } {2\sigma^2 + 2\frac{i\hbar t}{m}} \right] \mathrm{d}x \\ &= \sqrt{\frac{\sigma^2}{\pi[\sigma^4 + \frac{\hbar^2 t^2}{m^2}]}} \int\limits_{-\infty}^{\infty} \exp\left[ - \frac{ y^2 } {2\sigma^2 - 2\frac{i\hbar t}{m}} \right] [y + \frac{\hbar k_0}{m}t] \exp\left[ - \frac{ y^2 } {2\sigma^2 + 2\frac{i\hbar t}{m}} \right] \mathrm{d}y \\ &= \frac{\hbar k_0}{m}t \, \sqrt{\frac{\sigma^2}{\pi[\sigma^4 + \frac{\hbar^2 t^2}{m^2}]}} \int\limits_{-\infty}^{\infty} \exp\left[ - \frac{ y^2 } {2\sigma^2 - 2\frac{i\hbar t}{m}} \right] \exp\left[ - \frac{ y^2 } {2\sigma^2 + 2\frac{i\hbar t}{m}} \right] \mathrm{d}y \\ &= \frac{\hbar k_0}{m}t \, \sqrt{\frac{\sigma^2}{\pi[\sigma^4 + \frac{\hbar^2 t^2}{m^2}]}} \sqrt{\pi} \left[ \frac{1}{2\sigma^2 - 2\frac{i\hbar t}{m}} + \frac{1}{2\sigma^2 + 2\frac{i\hbar t}{m}} \right]^{-1/2} \\ &= \frac{\hbar k_0}{m}t \end{align}\]Therefore, the center of the wavepacket propagate with the group velocity
\[\begin{equation} v_g = \frac{\hbar k_0}{m} \end{equation}\]