- General description. 本课程是概率理论和数理统计的入门基础课程, 着重于在理解概率模型和统计方法中所必须的概率基础和统计思想学习. 课程内容包括概率公理,基础组合排列方法, 离散和连续随机变量, 概率分布, 数学期望,中心极限定理; 点估计方法, 包括矩估计方法, 极大似然估计方法等, 显著性检验方法, 包括一样本均值检验, t 检验和两样本均值检验, t检验, F检验等. 以及Pearson Chi-square检验方法等.
- Prerequisites. 高等数学,高等代数.
- Syllabus (教学大纲)
- Textbook. 概率论与数理统计(Probability and Statistics), 陈希孺编著,中国科学技术大学出版社.
- Assignments & tests. 作业将根据<<概率论与数理统计习题集>>选题, 本课程没有期中考试, 期末考试为全校联考.
- Course grade. 课程最终成绩由以下决定: 平时成绩35/100, 以及65/100期终考试
- 网上在线答疑
- 爱课程网本课程视频资源
- 第一章: 随机事件与概率
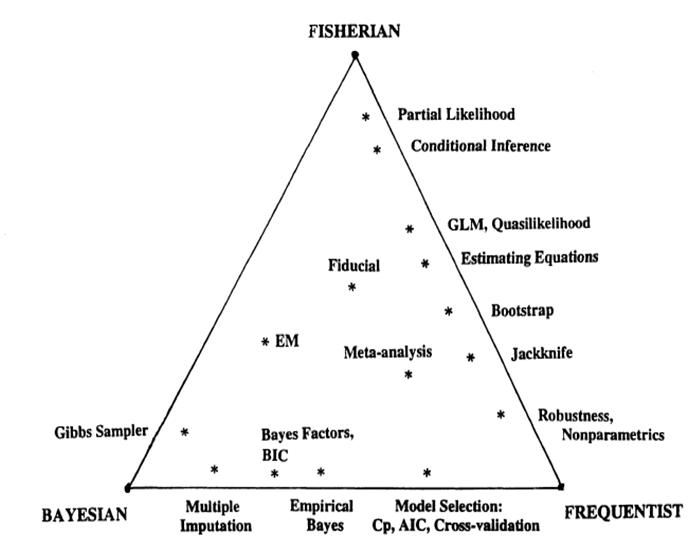
- 简介: Why Probability and Statistics--some examples.
- 1.1: 事件及其运算, 概率及其性质: slides
- 1.2:古典概型和几何概率: slides
- 1.3:条件概率与独立性: slides R examples 1
- 第一章讲义
- 第二章: 随机变量及其分布
- 2.1:离散型随机变量slides R examples
- 2.2:连续型随机变量 slides R examples 2
- 2.3:多维随机变量 slides R examples 3
- 2.4: 条件分布与独立性 slides
- 2.5:随机变量的函数的分布 slides
- 第二章讲义
- 第三章: 随机变量的数字特征
- 第四章: 大数律与中心极限定理
- 第五章: 数理统计的基本概念与抽样分布
- 第六章: 参数估计
- 第七章: 假设检验 R code demo
- 第一章: 随机事件与概率
- 第一讲:A short history of Probability; 课本P1-4, 19-22; Read " Chapter 1. The Role of Statistics in Engineering" of Douglas et. al. (2003); Wikipedia上概率的定义
- 第二讲: 课本P11-18, Wikipedia上Buffon's Needle ; Birthday Problem; 学报论文"浅谈概率中一般加法公式的应用";
- 第三讲: 课本P26-39 , Conditional Probability Pitfall ; Wikipedia上 Bayes's theorem; Monty Hall Problem
- 第二章: 随机变量及其分布
- 第一讲: 课本P44-53; Jacob Bernoulli 简介; Bernoulli 家族; Poisson 简介; Negative Binomial distribution; Coupon Collector's Problem;
- 第二讲: 课本P54-61; Normal distribution; Carl Friedrich Gauss; 数学王子高斯; Blaise Pascal; (百度百科); 概率分布关系图 正态分布的前世今生
- 第三讲: 课本P61-73; Multinomial distribution, Multivariate Normal distribution from Wikipedia; 二元正态分布图示 Brad Hartlaub’s page for bivariate normal distribution
- 第四讲: 课本P73-84;
- 第五讲: 课本P85-106;
- 第三章: 随机变量的数字特征
- 第一讲: 课本P112-128; 数学期望的应用一,二; 数学期望的应用举例; 平均数和数学期望; 论数学期望定义中“绝对收敛”
- 第二讲: 课本P129-144;
- 第四章: 大数律与中心极限定理
- 第一讲: 课本P145-150; 圣彼得堡概率论学派的中心极限定理思想研究; 概率论简史; 概率哲学思想的几次进化; 更多有关概率统计史请在CNKI中国学术期刊网上检索 "作者" "徐传胜".
- 第五章:数理统计的基本概念与抽样分布
- 第一讲: 课本P154-162; Chi-squre distribution; Student t distribution; Student's z, t, and s: What if Gosset had R?; F distribution
- 第二讲: 课本P100-106; 深交所蹊跷的新股中签概率:9‰的中签率要低于8‰中签率
- 第六章: 参数估计
- 第一讲: P163-172;P178-184; Point Estimation;
- 第二讲: P191-206; Confidence Interval; Estimation of Completion Rates
- 第七章: 假设检验
- 第一讲: P213-240;
- 第二讲: P241-254; P Values
- 第三讲: P260-271; Goodness of fit test; Karl Pearson; Sir R.A. Fisher
软件与例子:
(swf动画演示部分试验和分布, from Internet)
- 访问 http://www.r-project.org 下载 R for windows 并安装. 《 R导论》中文参考文档
- 下载 prob package: elementary probability on finite sample spaces (0.9.1) (CRAN : here) 并安装.
- 参阅例子和说明文件: here 或者在 R 命令窗口下用 vignette("prob")查看.
- 使用人大的谢益辉开发的R animation package (网址) 进行试验. (本地下载此package, 帮助文件)
- 第一章: 随机事件与概率
- n个人没有两个人生日相同的概率程序.
- Buffon投针试验程序(需要R animation package)
- 第二章: 随机变量及其分布
- 使用R里的二项分布命令产生一些二项分布的随机数,观察二项分布的分布函数形状; 对Poisson分布和负二项分布做类似的试验. (R code 范例)
- 使用R的正态分布命令(rnorm等)对正态分布的形状等进行研究. 生成二项分布和Poisson分布的随机数后,观察其直方图的形状随随机数个数的变化, 以及和正态分布形状的关系. 二元正态例子(R code)
- 第三章: 随机变量的数字特征
- 产生常见分布的随机数, 使用R计算其数字特征, 并试验偏度系数和峰度系数.
- 第四章: 大数律与中心极限定理
- 第五章:
数理统计的基本概念与抽样分布
- 熟悉chi-square, t和F分布的R命令.
- 第六章: 参数估计
- 仔细阅读 11/25-12/2 Reading list 中的Estimation of Completion Rates文章,利用R重复期中的模拟结果,看看结果是否一致.
- 第七章: 假设检验
- 熟悉 z.test( in Package" TeachingDemos") or write your own z.test function! t.test; var.test; prop.test; binom.test;, chisq.test; fisher.test;
R与其他学科: 总览
- R 与化学和计算物理
- Ron Wehrens, Chemometrics with R, Springer, 2011
- Eric D. Feigelson and G. Jogesh Babu,Modern Statistical Methods for Astronomy With R Applications,Cambridge, 2012
- D.C. Harris, Quantitative Chemical Analysis, 8th ed., W.H. Freeman & Co., New York, 2010.
- R 与环境计量学
- R 与高性能计算和并行计算