Research
Main content
A traditional focus of the group is on developing theories in stochastic thermodynamics. We have systematically studied nonlinear chemical dynamics in small systems such as the effects of internal noise in small chemical reaction systems, relaxation and glassy dynamics of a system of active particles. We also study the issue of stochastic thermodynamics and fluctuation theorems in mesoscopic oscillation systems.:
Some recent representative results are given as follows:
Design principles for biochemical oscillations with limited energy resources
As biochemical systems may frequently suffer from limited energy resources, internal molecular fluctuation has to be utilized to induce random rhythm, To understand the elementary principles for biochemical systems with limited energy resources to maintain phase accuracy and phase sensitivity, we address the issue by deriving the energy-accuracy and the sensitivity-accuracy trade-off relations for a general biochemical model, analytically and numerically. We find that biochemical systems have a much lower energy cost by using noise-induced oscillations to keep almost equal efficiency to maintain precise processes compared with the energy cost using normal oscillations, clearly elucidating a survival mechanism when energy resources are limited. Moreover, an optimal system size is predicted where both the highest sensitivity and highest accuracy can be reached at the same time, providing a new strategy for the design of biological networks with limited energy sources
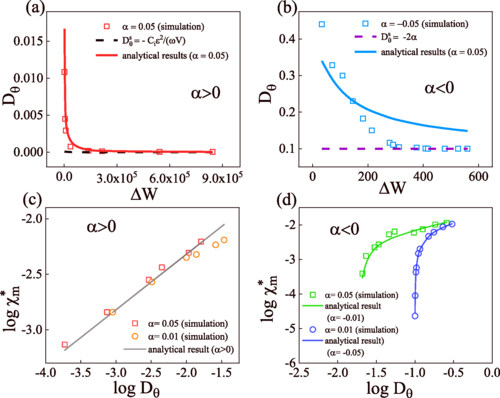
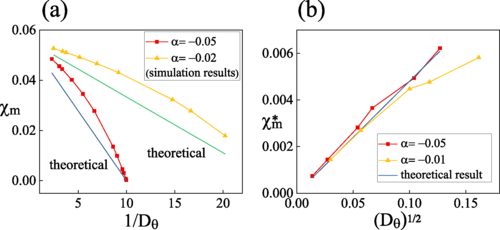
Phys. Rev. Research , 2, 043331
Mode-Coupling Theory Study of Glassy Dynamics in Active Particles System
We presented a mode coupling theory study for the relaxation and glassy dynamics of a system of strongly interacting self-propelled active particles, we find the critical density rc for given tp shifts to larger values with increasing magnitude of propulsion force or effective temperature, in good accordance with previously reported simulation work. In addition, We find thatTceff increases with tp and in the limittp - 0, it approaches the value for a simple passive Brownian system as expected.
Our theory also well recovers the results for passive systems and can be easily extended to more complex systems such as active–passive mixtures.
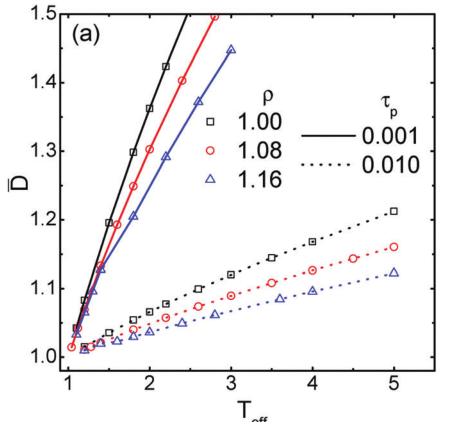
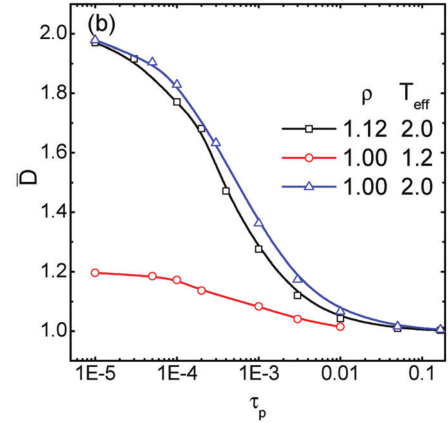
Soft Matter 2017, 13, 4464
Fluctuation Effect in a Genetic Toggle Switch
We find that a conventional biological genetic toggle switch can show an extra stable state, which locates around the unstable state predicted by ordinary differential equations. Detailed analysis based on stochastic nullclines shows that the smallness and discreteness of some critical molecule numbers play an important role
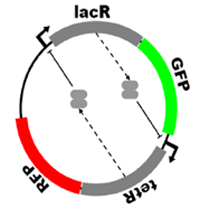
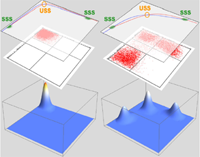
Phys. Rev. Lett. 2012 , 109, 248107
