
Teaser: Our approach is able to faithfully recover sharp features corrupted by noise. (a) The octa-flower model as a ground truth; (b) the model artificially corrupted by independent and identically distributed (i.i.d.) noise (with zero mean and standard deviation 1% of the diagonal of the bounding box of the model); (c) the error map of (b); (d) the denoising result by our approach; (e) the error map of (d). The colored models (c,e) visualize the errors between the processed models and the ground truth model (a). Note that sharp features such as creases and corners are well retained in our result (d).
Abstract
Many geometry processing
applications are sensitive to noises and sharp features. Although there
are a number of works on detecting noises and sharp features in the
literature, they are heuristic. On one hand, traditional denoising
methods use filtering operators to remove noises, however, they may blur
sharp features and shrink the object. On the other hand, noises make
detection of features, which relies on computation of differential
properties, unreliable and unstable. Therefore, detecting noises and
features on discrete surfaces still remains challenging.
In this paper, we present an approach for simultaneously decoupling
noises and features on 3D shapes. Our approach consists of two phases.
In the first phase, an estimated base mesh is generated to approximate
the true underlying surface of the input noisy mesh by a global
Laplacian regularization denoising scheme. The base mesh is guaranteed
to asymptotically converge to the underlying surface with probability
one as the sample size goes to infinity. In the second phase, an
l1-analysis
compressed sensing optimization is proposed to recover sharp features
from the residual between the base mesh and the input mesh. This is
based on our discovery that sharp features can be sparsely represented
in some coherent dictionary which is constructed by the pseudo-inverse
matrix of the Laplacian of the shape. The features are recovered from
the residual in a progressive way. Theoretical analysis and experimental
results show that our approach can reliably and robustly remove noises
and extract sharp features on 3D shapes.
Decoupling feature and noise is a chicken-and-egg problem:
-
Feature detection is unreliable in the presence of noise
-
Denoising (filtering) operations would blur sharp features
Observation and basic idea:
-
Sharp features are sparse in geometry
-
The tool of compressed sensing enables extract sparse signals
Phase I: Decouple the Base Smooth Surface and the Residual (denoising the mesh)
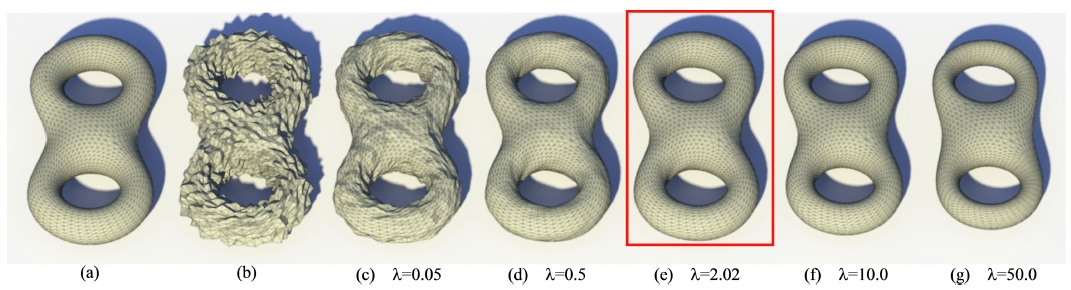
Figure 2. Our approach computes the optimal smoothness parameter to denoise the mesh. (a) the ground truth 8-like model which is a C2 smooth surface; (b) the model artificially corrupted by severe synthetic noise; (c)-(g) denoised results by the global smoothing approach with various parameters \lambda in the Laplacian smoothing model. Our approach obtains the best smoothing result (e) via the automatically chosen optimal parameter \lambda=2.02.
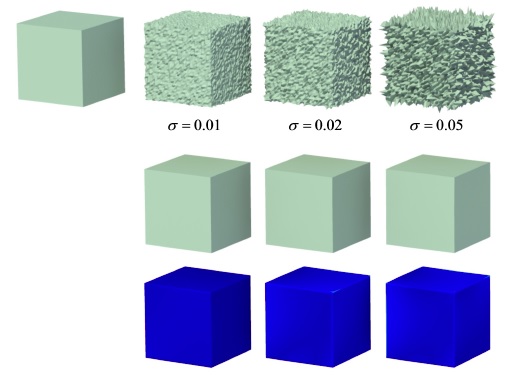
Figure 3. Our approach is robust to different levels of noise. For the cube model with sharp features, the first row shows the ground truth model followed by the noisy models with different levels of noise (the standard deviation is shown below each model), the second row shows the denoised models, and the third row visualizes the differences between the denoised models and the ground truth model.
Phase II: Decouple Feature and Noise from Residual

Figure 4. (a) The input noisy mesh model; (b) phase I: denoising the model; (c) phase II: recovering sharp features (shown in red dots) progressively based on L1-analysis compressed sensing; (d) the final denoised result with recovered features.

Figure 5. (a) the ground truth model; (b) the noisy model; (c) phase I: denoising the model; (d)-(e) phase II: recovering sharp features (shown in red dots) progressively based on L1-analysis compressed sensing; (f) the final denoised result with recovered features.
(at SIGGRAPH 2014)
PPT (1.5M)
News at USTC
We would like to thank the anonymous reviewers for their constructive
comments. The work is supported by the 973 Program 2011CB302400, the NSF of
China (nos. 11031007, 11171322, 61222206), One Hundred Talent Project of
the Chinese Academy of Sciences, the 111 Project (no. b07033), and the
Program for New Century Excellent Talents in University (no.
NCET-11-0881).
title = {Decoupling Noises and Features via Weighted L1-analysis Compressed Sensing},
author = {Ruimin Wang and Zhouwang Yang and Ligang Liu and Jiansong Deng and Falai Chen}
journal = {ACM Transactions on Graphics},
volume={33},
number={2},
pages={Article 18: 1-12},
year = {2014}
}