Primitive Cell to Supercell
Suppose the transformation matrix between the primitive cell ($\mathbf{A}$) and the supercell ($\mathbf{a}$) is $M$, i.e.
\[ \mathbf{A} = M\cdot \mathbf{a} \]
- For a simple supercell, $M$ is diagonal. Below is the matrix for 3x3x3 supercell.
\[ M = \begin{bmatrix} 3 & 0 & 0 \cr 0 & 3 & 0 \cr 0 & 0 & 3 \end{bmatrix} \]
- The matrix between a hexagonal and an orthogonal cell
\[ M = \begin{bmatrix} 1 & 0 & 0 \cr 1 & 2 & 0 \cr 0 & 0 & 1 \end{bmatrix} \]
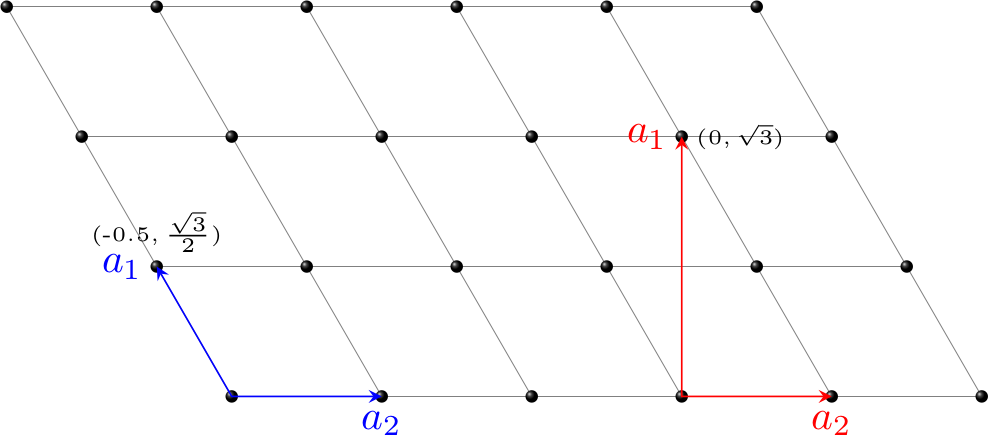
One way to generate the supercell is to use the tool provided by ASE, e.g.
1
2
3
4
5
6
7
8
from ase.io import read, write
from ase.build.supercells import make_supercell
M = [[1, 0, 0], [1, 2, 0], [0, 0, 1]]
pri_cell = read('primitive.vasp')
sup_cell = make_supercell(pri_cell, M)
write('supercell.vasp', sup_cell, vasp5=True, sort=True, direct=True)
Supercell to Primitive Cell
One way is to use phonopy to find the primitive cell, e.g.
1
phonopy --symmetry -c POSCAR
From the supercell in POSCAR, you get a primitive cell output in the file PPOSCAR.
